Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 1
Usando os dados da Tabela 2.1, Capítulo 2:
(a) Construa a distribuição de freqüência conjunta para as variáveis grau de instrução e região de procedência.
(b) Qual a porcentagem de funcionários que têm o ensino médio?
(c) Qual a porcentagem daqueles que têm o ensino médio e são do interior?
(d) Dentre os funcionários do interior, quantos por cento têm o ensino médio?
Passo 1
(a) Construa a distribuição de freqüência conjunta para as variáveis grau de instrução e região de procedência.
Vamos lá... mas pera aí, o que seria distribuição de frequência conjunta?
Para explicar, vamos direto ao ponto, beleza?
Em muitos casos temos interesse em analisar o comportamento de mais de uma variável aleatória. Nestes casos, devemos utilizar a DISTRIBUIÇÃO DE FREQUÊNCIA CONJUNTA. Essa distribuição nos dá o comportamento simultâneo de mais de uma variável aleatória 😉.
Ah... então nós precisamos contruir uma tabelinha que relacione as variáveis grau de instrução e região de procedência, certo?
Seja:
Construindo a tabela...
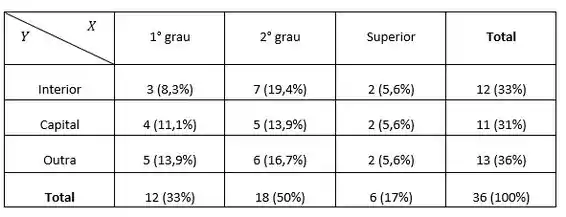
Notem que para ecomonizar tempo, na tabela já se encontram os valores das frequências absolutas e relativas 😉.
Passo 2
(b) Qual a porcentagem de funcionários que têm o ensino médio?
Basta olharmos para a nossa tabela.
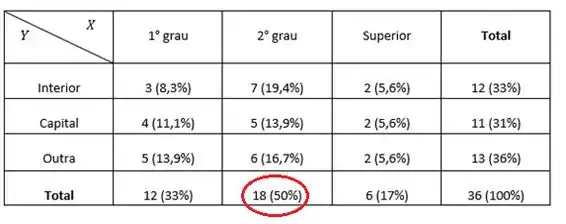
Logo
Passo 3
(c) Qual a porcentagem daqueles que têm o ensino médio e são do interior?
Novamente, basta olharmos para a nossa tabela.
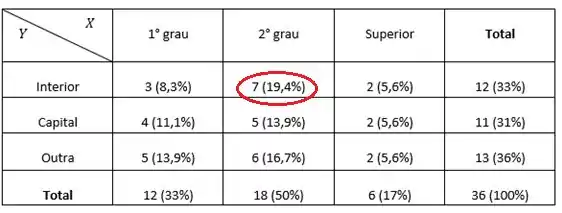
Logo
Passo 4
(d) Dentre os funcionários do interior, quantos por cento têm o ensino médio?
Opa! Vocês concordam comigo que agora queremos uma probabilidade condicional?
Queremos , certo?
Beleza... mas muda o que? Muda que agora temos que considerar apenas aqueles que são do interior.
Sabemos que . Trazendo para o nosso problema, temos
Resposta
(a)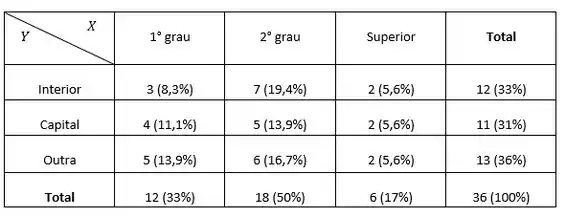 
(b) 50%
(c) 19,4%
(d) 58,3%