Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 28
Para verificar se a força de empuxo na perfuração é influenciada pela velocidade da perfuração (A), pela taxa de alimentação (B) ou pelo material usado (C), foi realizado um experimento usando quatro velocidades, três taxas e dois tipos de material, com duas amostras ( 2) perfuradas em cada combinação de níveis dos três fatores. As somas dos quadrados foram calculadas como a seguir: , .
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Elabore uma tabela ANOVA e identifique interações significativas usando . Por acaso algum fator isolado parece não exercer nenhum efeito sobre a força de empuxo? (Em outras palavras, algum fator parece não-significativo em todos os efeitos em que aparece?)
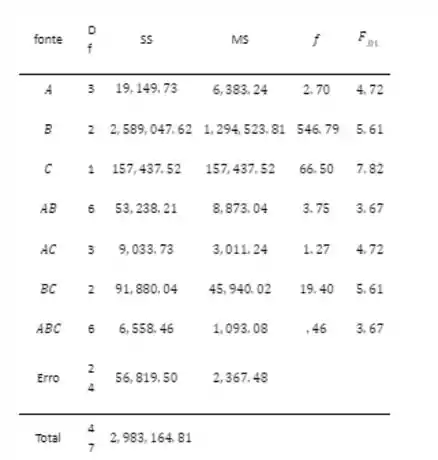
As interações estatisticamente significativas são AB e BC. O fator A parece ser o menos significativo de todos os fatores. Não tem um efeito principal significativo e a interação significativa (AB) é apenas um pouco maior que o valor tabelado no nível de significância 0,01
Resposta
valor tabelado no nível de significância 0,01
Espero que tenham aprendido com essa questão, até a próxima !