Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 41
a. Verifique que E( ˆ 1) 1 usando as regras do valor esperado do Capítulo 5. b. Use as regras de variância do Capítulo 5 para verificar a expressão para V( ˆ 1) fornecida nesta seção.
Passo 1
-
Para o modelo de regressão linear simples o valor esperado é
A estimativa de mínimos quadrados da inclinação é
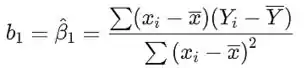
Obviamente, o valor esperado de é
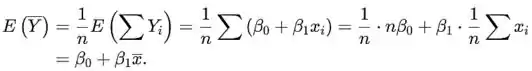
Por fim, para verificar a alegação
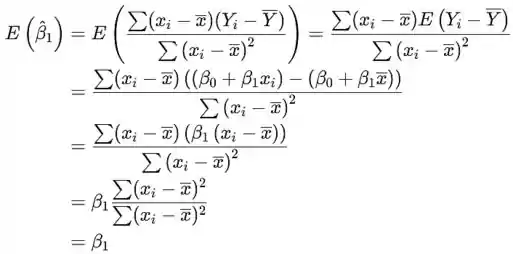
que verifica a alegação
Passo 2
Este pode ser complicado. Lembre-se que as variáveis aleatórias são independentes e que a variância de é
De
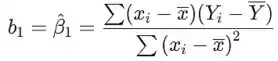
separe o denominador e observe que
Passo 2
O seguinte vale
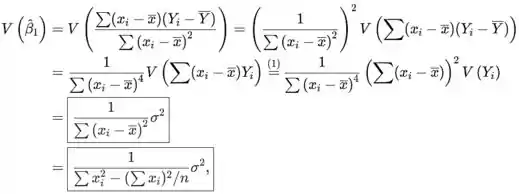
Resposta
Ver o desenvolvimento
Exercícios de Livros Relacionados
A tabela abaixo indica o valor y do aluguel e a idade x de cinco casas.c) Qual o significado do coeficiente angular nesse caso?
Usando os dados do Exemplo 15.1 : b) Interprete o significado de α e β nesse problema.
Usando os dados do Exemplo 15.1 : Encontre a reta de mínimos quadrados z i ^=α+β x i , ondez mede a acuidade visual e x , a idade.
Usando os dados do Exemplo 15.1 : c) Para cada indivíduo, encontre o desvio e ^ i = z i - z ^ i existe algum com valor muito exagerado?
A tabela abaixo indica o valor y do aluguel e a idadex de cinco casas.b) Faça o gráfico dos pontos e da reta ajustada. Você acha que o modelo adotado é razoável?