Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 44

Ao ajustar o modelo de regressão linear simples para as n = 27 observações sobre x = módulo de elasticidade e y resistência à flexão, no Exercício 15 da Seção 12.2, obtivemos yˆ 7,592, sˆ Y 0,179 quando x 40 e yˆ 9,741, sˆ Y 0,253 para x 60. a. Explique por que sˆ Y é maior quando x 60 do que quando x 40. b. Calcule um intervalo de confiança com um nível de confiança de 95% para a resistência média real de todas as vigas cujo módulo de elasticidade é 40. c. Calcule um intervalo de previsão com um nível de previsão de 95% para a resistência de uma única viga cujo módulo de elasticidade é 40. d. Se for calculado um IC de 95% para a resistência média real quando o módulo de elasticidade é 60, qual será o nível de confiança simultâneo para ambos os intervalos calculados na parte (b)?

Passo 1

  1. S y ^ é maior para x=60 comparado com x=40, porque x=40 está mais próximo da média de todos os valores x do que x=60 e então os valores previstos são menos propensos a variar do que ainda mais da média
  2. Dado:

    3. c = 95 = 0.95

    Os graus de liberdade são o tamanho da amostra reduzido em 2:

    d f = n - 2 = 27 - 2 = 25

    O valor t crítico pode ser encontrado na tabela de distribuição T de Student no apêndice na linha de d f = 25 e na coluna de α = 1 - c / 2 = 0.025   :

    t * = 2.060

    Os limites do intervalo de confiança tornam-se então:

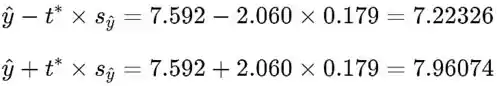
    Passo 2

  3. c = 95 % = 0.95

    4. O erro quadrático médio é a soma dos erros quadráticos dividido pelo tamanho da amostra reduzido por 2:

    s 2 = M S E = S S E n - 2 = 18.7356 27 - 2 ≈ 0.7494

    O erro padrão da estimativa é a raiz quadrada do erro quadrado médio.

    s = M S E = 0.7494   ≈ 0.8657

    Os graus de liberdade são o tamanho da amostra reduzido em 2:

    d f = n - 2 = 27 - 2 = 25

    O valor t crítico pode ser encontrado na tabela de distribuição T de Student no apêndice na linha de d f = 25 e na coluna de α = 1 - c / 2 = 0.025 :

    t * = 2.060

    Os limites do intervalo de confiança tornam-se então

    Passo 3

Ambos os intervalos de confiança têm um nível de confiança de 95%. α é o complemento do nível de confiança.

α = 1 - c = 1 - 95 % = 1 - 0.95 = 0.05

A desigualdade de Bonferroni então nos diz que o nível de confiança conjunto ou simultâneo é garantido como sendo pelo menos 100 ( 1 - k α ) % com k o número do intervalo de confiança.

No nosso caso: k = 2 e α = 0.05 :

100 ( 1 - k α ) % = 100 ( 1 - 2 ( 0.05 ) ) % = 90 %

Resposta

  1. x = 40 está mais próximo da média de todos os valores x do que x=60
  2. (7.22326,.9604)
  3. (5.7709,9.4131)
  4. Pelo menos 90%

Exercícios de Livros Relacionados

Os dados abaixo correspondem às variáveis renda familiar e gasto com alimentação numa amostra de dez famílias, representadas em salários mínimos. Obtenha a equação de regressãoy ^ = α ^ + β ^ x .b) Qu
Com o modelo z ^ = α ^ + β ^ x para a acuidade visual, desenvolvido nos problemas anteriores:b) construa o I C de 95 % para a acuidade visual esperada para indivíduos com30 anos de idade;
Com o modelo z ^ = α ^ + β ^ x para a acuidade visual, desenvolvido nos problemas anteriores:Construa o I C de 95 % para a acuidade visual média dos indivíduos com 18 anos de idade;
O custo de manutenção de tratores parece aumentar com a idade do trator. Os seguintes dados foram obtidos ( X representa idade em anos e Y o custo por seis meses):d) Teste as hipóteses H 0 :β 0=300 ,H
Os dados abaixo correspondem às variáveis renda familiar e gasto com alimentação numa amostra de dez famílias, representadas em salários mínimos. Obtenha a equação de regressãoy ^ = α ^ + β ^ x .Qual