Teste de Homogeneidade
Produzido por Jorge Alberto NascimentoTeoria
Teste de Homogeneidade
Na primeira etapa vimos o caso em que a gente queria testar a hipótese de que a amostra seguia a distribuição da população, (no caso se o dado era viciado ou não).
Nesse caso aqui te faço uma nova indagação, imagine duas turmas diferentes, ensinadas pelos mesmos professores, que fizeram as mesmas provas, e tudo igual blablabla. O que esperamos é que as notas das duas turmas possuam uma relação certo?
O que vamos fazer aqui é testar se duas amostras da mesma população seguem a mesma distribuição.
Mas voltamos a aquela famosa pergunta. Qual hipótese devemos testar? Será uma bem parecida com o teste de aderência visto antes, mas em vez de comparar a probabilidade obtida com a esperada, compararemos a probabilidade obtida de um grupo com a do outro grupo.
Onde:
pi = Probabilidade observada para o valor i, na primeira amostra
i = Probabilidade observada para o valor i, na segunda amostra
S = Número de casos possíveis.
Até aqui de boas? Então vou deixar mais de boas ainda, a estatística de teste que a gente vai usar, é a mesma!! Isso mesmo pode comemorar.
Onde:
Oi = Número de casos ocorridos para o valor i
Ei = Número de casos esperados para o valor i
E o mais legal rejeitaremos H0 no mesmo caso do anterior, isto é:
Onde:
Mas ai tu me pergunta, como diabos vamos achar o valor de Ei e qual valor de Oi vamo usar? Pera, pera uma pergunta de cada vez, nada que assuste.
No caso do Oi você escolherá todos os valores encontrados em ambos os grupos, vai ficar muita conta mas eu sei que você consegue =).
Agora qual Ei, nada para se assustar também, basta fazer a média entre os dois valores encontrados pra cada grupo distinto.
Vamos fazer um exemplo aqui para deixar mais claro
Ex: Em uma das maiores faculdades do país (a sua 😉), duas turmas sobre as mesmas condições fizeram uma prova de teste de adesão, e os resultados foram os seguintes

NA = 50 alunos turma A
NB = 50 alunos turma B
S = 5 resultados possíveis (faixas de notas possíveis)
α = 5% de significância
Vamos achar o valor esperado para cada caso possível, chamaremos i=1 para o intervalo [0,2), i=2 para o invervalo [2,4) e assim sucessivamente
Agora jogando os dados na nossa estatística de teste teremos:
Não sei se você percebeu mas temos um macete aqui, cada valor se repete uma vez, então, em vez de fazermos essa conta toda, podemos escolher uma das duas turmas e multiplicar cada resultado por 2. Esperto né?
Agora olhando o :
Como , não rejeitamos H0 a um nível de significância 5%, então temos evidências que as notas das turmas seguem a mesma distribuição.
Exercícios Resolvidos
Exercício Resolvido #1


Passo 1
Aqui teremos que aplicar o teste de homogeneidade para as duas escolas, e ver se elas são homogêneas a um nível de significância 1% e depois obter o p-valor dessa amostra. Lembre-se que precisamos encontrar o valor esperado para cada caso.
Passo 2
Encontrando o valor esperado para cada caso Ei:
Passo 3
Agora vamos aplicar os dados na estatística de teste:
Passo 4
Agora vamos achar na tabela da qui-quadrada o quantil 99% com 3 graus de liberdade
Passo 5
Comparando agora os dois valores encontrados temos que:
Logo a um nível de significância de 1% não rejeitamos H0, isto é, temos evidência que as duas populações são homogêneas.
Passo 6
Agora para acharmos o p-valor bastar olharmos o resultado que encontramos na amostra 9,462 na tabela da qui-quadrada com 3 graus de liberdade.
Ao fazermos isso vemos que o p-valor está entre o 0,025 e 0,010. Logo p-valor=[0,010; 0,025]
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2

Teste a um nível de significância α=0,05
Passo 1
Aqui teremos que aplicar o teste de homogeneidade para os dois métodos, e ver se eles são homogêneas a um nível de significância 5%. Lembre-se que precisamos encontrar o valor esperado para cada caso.
Passo 2
Encontrando o valor esperado para cada caso Ei:
Passo 3
Agora vamos aplicar os dados na estatística de teste:
Passo 4
Agora vamos achar na tabela da qui-quadrada o quantil 95% com 1 graus de liberdade
Passo 5
Comparando agora os dois valores encontrados temos que:
Logo a um nível de significância de 5% não rejeitamos H0, isto é, temos evidência que os dois métodos são homogêneos.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3

Teste a um nível de significância α=0,05
Passo 1
Aqui teremos que aplicar o teste de homogeneidade para as duas drogas, e ver se elas são homogêneas a um nível de significância 5%. Lembre-se que precisamos encontrar o valor esperado para cada caso.
Passo 2
Encontrando o valor esperado para cada caso Ei:
Passo 3
Agora vamos aplicar os dados na estatística de teste:
Passo 4
Agora vamos achar na tabela da qui-quadrada o quantil 95% com 1 graus de liberdade
Passo 5
Comparando agora os dois valores encontrados temos que:
Logo a um nível de significância de 5% não rejeitamos H0, isto é, temos evidência que as duas drogas são homogêneos.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4

Teste a um nível de significância α=0,01
Passo 1
Aqui teremos que aplicar o teste de homogeneidade para as duas cidades, e ver se a aceitação do produto é homogênea a um nível de significância 1%. Lembre-se que precisamos encontrar o valor esperado para cada caso.
Passo 2
Se das 100 pessoas da cidade A, 32 gostaram do produto, o número de pessoas que não gostaram do produto na cidade A é de:
100 – 32 = 68
Se das 50 pessoas da cidade B, 12 gostaram do produto, o número de pessoas que não gostaram do produto na cidade B é de:
50 – 12 =38
Passo 3
Encontrando o valor esperado para cada caso Ei:
Passo 4
Agora vamos aplicar os dados na estatística de teste:
Passo 5
Agora vamos achar na tabela da qui-quadrada o quantil 99% com 1 graus de liberdade
Passo 6
Comparando agora os dois valores encontrados temos que:
Logo a um nível de significância de 1% rejeitamos H0, isto é, temos evidência que as duas drogas não são homogêneas.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Na indústria cerâmica, avalia-se sistematicamente a resistência de amostras de massas cerâmicas, após o processo de queima. Dessas avaliações, sabe-se que certo tipo de massa tem resistência mecânica aproximadamente normal, com média e variância Após a troca de alguns fornecedores de matérias- primas, deseja-se verificar se houve alteração na qualidade. Uma amostra de corpos de prova de massa cerâmica acusou média igual a . Qual é a conclusão ao nível de significância de ?
Passo 1
Queremos testar se houve alteração na qualidade, ou seja, se a média é diferente de . Então nossa hipótese nula vai ser:
Nada foi dito se é maior ou menor que isso, então usamos só o mesmo.
E a alternativa, é justamente o que queremos testar:
Então estamos num teste bilateral.
Passo 2
No bilateral, nossa estatística de teste é dada por:
No nosso caso, substituindo os valores do enunciado, ficamos com:
Lembrando que o foi dado foi a variância que vale , então o é a raiz disso, ou seja, .
Passo 3
No bilateral, nossos pontos críticos são:
É pedido um nível de significância de , então:
Portanto:
Então nossa região crítica fica sendo:
Passo 4
Então desenhando nossa região crítica e vendo a localização da nossa estatística de teste:
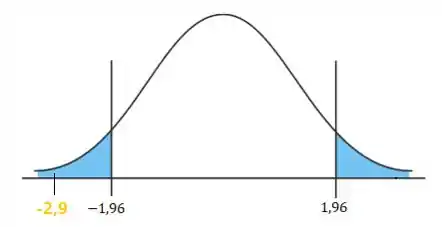
Vemos que ela cai dentro da , ou seja, rejeitamos a hipótese nula!
Resposta
Exercício Resolvido #6

Passo 1
Aqui teremos que aplicar o teste de homogeneidade para os dois gêneros, e ver se a preferência ao adoçante é homogêneas, como ele não dá um nível de significância vamos tirar as conclusões diretamente do p-valor dessa amostra. Lembre-se que precisamos encontrar o valor esperado para cada caso.
Passo 2
Encontrando o valor esperado para cada caso Ei:
Passo 3
Agora vamos aplicar os dados na estatística de teste:
Passo 4
Agora para acharmos o p-valor bastar olharmos o resultado que encontramos na amostra (101,754) na tabela da qui-quadrada com 2 graus de liberdade.
Ao fazermos isso vemos que não temos na tabela uma região que clara de onde o p-valor está, mas conseguimos perceber que ele é muito baixo.
Passo 5
Agora interpretando esse resultado:
O p-valor é o menor valor que rejeita H0, logo se esse valor é extremamente baixo, tiramos a conclusão que praticamente todo α que escolhermos rejeitará a hipótese nula. Então como rejeitamos a hipótese temos evidência que a distribuição da preferência pelos dois sexos não é a mesma.
Resposta
Ei, a resposta está no passo a passo :)