Estruturas de Repetição: O laço For
Produzido por Gustavo BarbosaTeoria
E aí pessoal, aqui é o Juan do Responde Aí, e hoje vamos falar de mais uma estrutura de repetição.
O laço for
Assim como nos laços e , a função do comando é repetir um determinado trecho de código enquanto uma expressão for verdadeira.
A grande diferença do laço é que ele permite declarar o início da variável de iteração, a expressão de teste e o incremento da variável de uma maneira mais fácil. Olha só como um laço é declarado:

Dentro dos parêntesis do laço a gente informa o ponto de início do loop, a condição de parada, e a condição de atualização da variável. Cada uma das partes é separada por um ponto-e-vírgula ().
Vou te mostrar um exemplo, que torna tudo mais fácil.
Exemplo 1: Crie um programa que conte de 1 até 10.
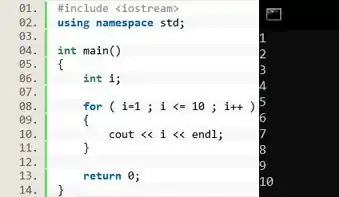
Primeiramente, na linha 06, a gente declarou uma variável para criar nossa iteração.
Na linha 08 criamos o nosso laço . Note que dentro dos parêntesis a gente diz que a variável vai começar com o valor . Em seguida indicamos que o laço deve se repetir enquanto for menor ou igual a , dessa forma . E antes de fechar o parêntesis informamos o tipo de incremento da variável , que no caso é somar uma unidade.
Depois, dentro das chaves, colocamos o código que queremos repetir.
Muitos programadores acham essa forma de criar loops mais fácil e enxuta, e por isso os loops são os mais utilizados.
Vamos fazer mais um exemplo:
Exemplo 2: Crie um programa que imprima somente os números pares de 0 à 20.
Primeiro a gente declara uma variável contadora . Em seguida iniciamos um laço em que a variável contadora inicia em , o laço deve se repetir enquanto o for menor ou igual a , e o deve aumentar de dois em dois .
O resultado é o código abaixo.
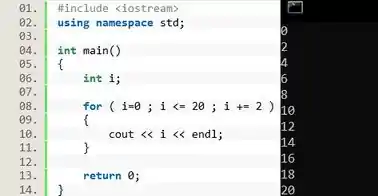
Note que o primeiro e o segundo código são bem parecidos. Todas as diferenças estão concentradas na declaração do na linha 08.
For... while... do-while... Qual escolher?
Essa é uma pergunta legal. Sendo bem pragmático, qualquer um dos laços é capaz de fazer tudo que os outros fazem. Porém, cada um deles tem certas vantagens que podem deixar a codificação mais fácil.

A estrutura do laço necessita de um ponto de início, ponto de fim, e condição de incremento. Então, ele costuma ser utilizando quando já sabemos quantas repetições serão necessárias. Ou seja, quando a questão pedir algo do tipo “faça um certo número específico de iterações” ou então “itere iniciando no número até um o número ”, o laço deve ser a melhor opção.
O laço é mais usado quando não temos o número exato de repetições, ou quando queremos gerar loops infinitos de propósito. Então se a questão pedir “faça iterações até o usuário dizer que não quer mais”, o laço provavelmente é a melhor escolha.
E por último, o laço é usado pra garantir que o laço será executado ao menos uma vez.
E basicamente, essa é a diferença entre os loops.

E por hoje é isso pessoal. Agora vamos ver uns exercícios de fixação.
For... while... do-while... Qual escolher?
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado de UFRN – Exercício de Aprendizagem nº3 – DCA800 – Questão 01
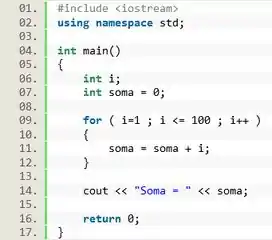
Utilize um loop para calcular a soma dos números naturais de 0 a 100.
Passo 1
Vamos nessa, galera!
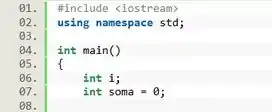
A questão é bem boazinha, e já diz pra gente qual laço devemos usar: o . O que vamos fazer é criar duas variáveis, uma pra guardar o valor da somado, chamada , e outra pra ser a variável contadora do nosso loop, chamada .
A variável vai começar com o valor , e a cada iteração do laço vamos adicionar o valor de na variável . Como a variável contadora assume os valores de 0 a 100 quer a gente quer somar, vamos usar ela pra essas 2 funções: controlar o loop e somar os números.
Então vamos declarar a variável contadora que deve ser do tipo inteiro. E como estamos somando números inteiros, vamos declarar a variável do tipo inteiro inicializada com o valor .
Passo 2
Agora vamos construir o nosso loop.
Primeiro vamos iniciar a variável contadora no valor , pois o nosso objetivo é somar os valores de , então não há necessidade de começar do zero.
A questão pede pra somar de zero até cem, então o loop deve continuar enquanto for menor ou igual a . Quando o valor de atingir 101, o loop deve ser quebrado.
Por fim, o valor de tem que aumentar de um em um, então vamos usar o operador de incremento
E isso tudo a gente escreve ali na linha 09, quando iniciamos o . Dentro do parênteses à direita do , escrevemos o valor inicial da variável (, o critério para que continuemos dentro do loop () e o comando pra incrementar a variável em 1 a cada rodada (). As 3 informações separadas por ponto e vírgula.
![]()
Dentro do laço vamos escrever nossa operação.
Para cada iteração nós vamos adicionar o valor ao valor já existente na variável . E o valor desse resultado vai ser atribuído como um novo valor à variável . Então podemos usar a seguinte expressão:
![]()
E com isso a gente termina o nosso laço.
Passo 3
Pra finalizar a questão, vamos exibir o valor calculado. Pra isso é só a gente usar o .
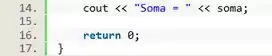
Cuidado pra não escrever esse comando dentro do loop, senão seu programa vai imprimir 100 mensagens pro usuário.
E prontinho! Questão finalizada.
Resposta
Exercício Resolvido #2
Adaptado de UFRN – Exercício de Aprendizagem nº3 – DCA800 – Questão 03
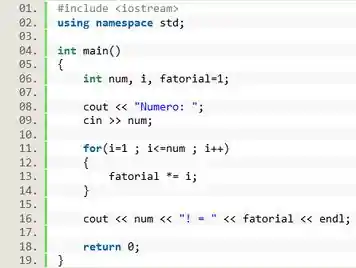
Faça um programa para calcular o fatorial de um número qualquer
Passo 1
Lets go, pessoal! Primeiro vamos relembrar o que é um fatorial.
O fatorial de um número é igual ao produto de todos os números inteiros de 1 ao ele mesmo. Por exemplo, o fatorial de é:
Em termos matemáticos é assim:
Passo 2
O que vamos fazer é criar um laço , neste laço, uma variável de iteração irá crescer de 1 até um certo número determinado pelo usuário.
Uma variável chamada vai começar com o valor , e a cada iteração do laço vamos multiplicar o valor de pelo valor guardado na variável .
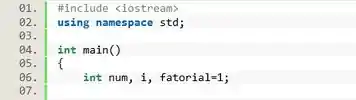
Então vamos declarar a variável que recebe o número do usuário , a variável de iteração , e declarar a variável que vai guardar o valor das multiplicações.
Só iremos trabalhar com números inteiros, então todas as variáveis serão do tipo
Passo 3
Pra começar, vamos usar o para pedir um número pro usuário, e com vamos armazenar o valor na variável
![]()
Passo 4
Agora é hora do show! Vamos construir nosso laço!
Como vamos realizar várias multiplicações, nosso loop deve começar em , se você começar o loop em as multiplicações vão ser todas zeradas, e não vamos conseguir calcular o fatorial.
As iterações vão acontecer enquanto for menor ou igual ao digitado pelo usuário. Assim, incluiremos todos os números necessários no fatorial
Por fim, o valor de tem que aumentar de um em um, então vamos usar o operador de incremento
![]()
Vamos escrever nossa operação dentro do laço. Para cada iteração nós vamos multiplicar o valor pelo valor da variável . Então podemos usar o operador de atribuição para executar a operação:
![]()
E com isso o laço esta prontinho!
Passo 5
Pra finalizar a questão, vamos exibir o valor do fatorial. Pra isso é só a gente usar o pra exibir o número digitado pelo usuário, seguido do símbolo “!”. E depois exibimos o valor do fatorial.

E questão pronta!
Resposta
Exercício Resolvido #3
Elaboração Própria
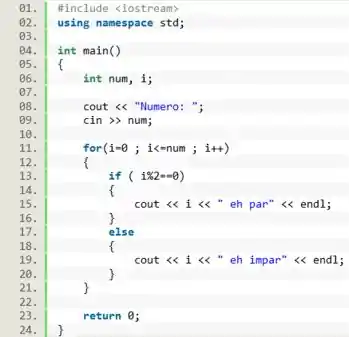
Faça um programa que receba um número do usuário, e em seguida imprima todos os números de até dizendo quais números são pares e quais são impares:
Seu resultado deve ser parecido com esse exemplo:

Passo 1
Vamos lá!
O que precisamos fazer é criar um laço que testes todos os números de até , e verifique se eles são pares ou ímpares. Ou seja, vamos usar um dentro de um laço
Então, vamos começar declarando duas variáveis. Uma variável inteira chamada será o nosso contador de voltas do loop. E uma outra variável inteira chamada que usaremos pra guardar o valor inserido pelo usuário.
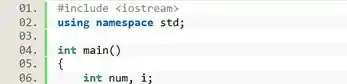
Passo 2
Pra começar, vamos usar o para pedir um número pro usuário, e com vamos armazenar o valor na variável
![]()
Passo 3
Agora vamos construir nosso laço
A questão nos pede pra testar todos os números partindo de zero, então o início do laço é em . O laço deve rodar enquanto for menor ou igual ao . E a variável deve aumentar de um em um, então vamos usar o incremento
![]()
Dentro do laço vamos ter que construir duas condições. Quando o número for divisível por 2, ele é par, caso contrário, ele é impar. Usando a estrutura podemos escrever:
SE FOR IGUAL A ENTÃO: Imprima que é par.

CASO CONTRÁRIO: Imprima que é impar
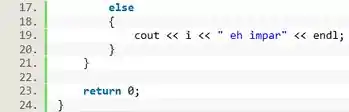
Por fim, fechamos o nosso laço e o programa está finalizado.
Resposta
Exercício Resolvido #4
Elaboração própria
Dada a seguinte série:
Onde: é um número real qualquer e é um número natural.
Faça um programa que receba o valor de e o valor de e imprima todos os membros do somatório, e diga qual é o resultado da soma.
Por exemplo. Pra e a saída deve ser:
![]()
Passo 1
Vamos lá pessoal.
Essa questão envolve bastante matemática. Então vamos logo incluindo a biblioteca
Pra efetuar um somatório podemos usar o laço , usando como nossa variável de iteração indo de 0 até . O detalhe dessa questão está na forma de exibir o resultado pro usuário. Mas fica tranquilo que eu te mostro como fazer.
Mas antes de tudo, vamos declarar nossas variáveis. é a variável de iteração, é o valor final das iterações que receberemos do usuário, é o valor constante da série, e é a variável onde vamos guardar nosso resultado. Como a variável soma vai sofrer operações de atualização, devemos inicia-la com valor zero.
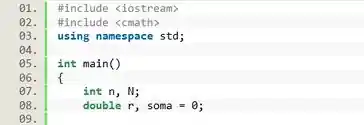
Passo 2
Agora vamos pedir os dados pro usuário. Usamos o para pedir os valores pro usuário, e com vamos armazenar o valor nas variáveis adequadas.

Passo 3
Agora vamos começar a exibir nossos resultados. Vamos dar uma olhada no exemplo que a questão trás
![]()
Perceba uma coisa, as partes que estão circuladas de azul são estruturas repetitivas: “um número seguido do sinal de adição +”. Em contrapartida, as partes circuladas de verde não apresentam nenhum padrão de repetição.
Vamos generalizar isso pra uma situação de N números
![]()
Note as partes circuladas em azul, há um padrão de escrita iniciando em e que se repete até : um número seguido do sinal de adição +. Já as partes circuladas em verde continuam sem apresentar nenhum padrão.
Isso diz pra gente, que dentro do laço vamos considerar apenas as partes circuladas em azul, e as partes circuladas em verde serão calculadas e escritas fora do laço.
Então, primeiro vamos escrever pro usuário “”:
![]()
Passo 4
Certo! Agora vamos criar um laço. Ele vai começar quando e vai enquanto for menor do que . E a variável será incrementada de um em um: .
![]()
Dentro do laço a gente vai somar o valor já existente na variável soma, com o valor . Pra isso podemos usar a função da seguinte forma:
![]()
Ainda dentro do loop, vamos usar o pra exibir os valores que estão sendo somados. Note que não usamos o pois queremos exibir tudo na mesma linha.
![]()
Isso finaliza o nosso loop.
Passo 5
O loop está concluindo, mas lembre-se, o nosso loop foi só até , ou seja, ainda falta somar no momento que .
![]()
E por fim, precisamos adicionar a exibição da última parcela da série, e o resultado final.
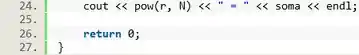
E pronto. Questão finalizada!
Resposta
Exercício Resolvido #5
Universidade de São Paulo – SSC-102 – Profa. Rosana T. Vaccare Braga – Lista de Exercícios 2 – Programas com estruturas de repetição – Questão 09
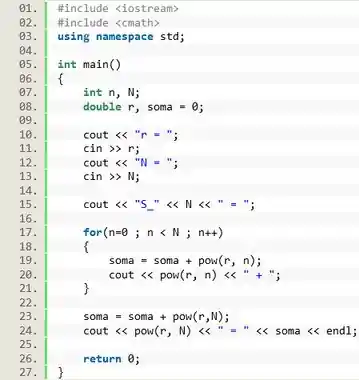
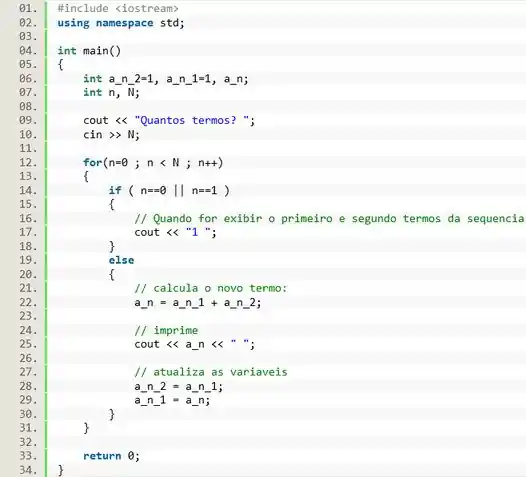
Faça um programa para gerar os n primeiros termos da seqüência:
Passo 1
A sequência mostrada na questão é conhecida como Sequência Fibonacci, e é muito importante no estudo das ciências naturais, como a física e a biologia. Nessa sequência o primeiro termo é e o segundo termo é . E daí por diante, cada número é a soma dos dois números anteriores. Ou seja, a sequência é dada pela relação:
Então, vamos lá declarar nossas variáveis.
Como usaremos um loop vamos precisar de uma variável de iteração . Também será necessária uma variável inteira para receber o número de termos que o usuário quer imprimir.
Para efetuar a Sequência Fibonacci vamos precisar de três variáveis: para representar o termo . A variável para representar o termo . E a variável para representar o termo .

Passo 2
Pra começar, vamos usar o para pedir um número pro usuário, e com vamos armazenar o valor na variável
![]()
Passo 3
Agora vamos criar o nosso loop
O primeiro termo da sequência ocorre em
![]()
Saca só, quando e , nós não precisamos fazer nenhum cálculo. Só temos que imprimir os termos e , então podemos usar uma condição para esses casos especiais

Show! E pra todas as outras possibilidades a gente vai efetuar o cálculo. Então abrimos um comando , assim todos os outros termos da sequência, que não vão entrar no da linha 14, vão entrar no . Dentro do , na linha 22, adicionamos a expressão a expressão pra calcular o próximo termo. E na linha 25, imprimimos o valor desse novo termo.

Ainda dentro do , vamos ter que atualizar os valores das variáveis e a_n_2, para podermos calcular o próximo . O valor contido em será enviado pra ; e o valor de será enviado pra . Isso é necessário para preparar os as variáveis para a próxima iteração do laço! Olha só como fica:
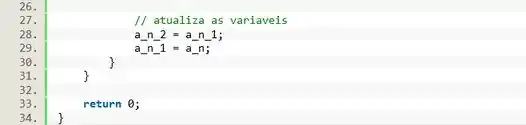
E pronto! Depois de fechar as chaves do e do laço a questão está concluída.
Resposta
Exercício Resolvido #6
UFRN – DCA800 – Exercício de Aprendizagem nº3 – Questão 6
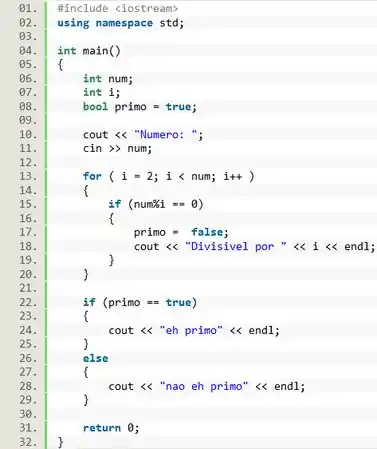
Ler um número e escreva se ele "é primo" ou "não é primo".
Passo 1
E aí galera, vamos resolver mais um exercício de fixação?!
Primeiro de tudo, você deve lembrar que um número primo é qualquer número inteiro e positivo que só seja divisível por 1 e por ele mesmo.
Então, uma forma de testar se um número é ou não é primo é tentando dividir esse número por todos os números que vem antes dele. Se em alguma tentativa o resta da divisão for zero, então esse não é um número primo.
Então vamos criar um programa que usa o operador de resto da divisão (). Por exemplo: pois é divisível por . Por outro lado, pois não é divisível por .
Pra começar, vamos escrever o cabeçalho do código:
![]()
Passo 2
Vamos declarar as variáveis do código.
De cara, a gente vai precisar de uma variável inteira para receber o número do usuário. E para desenvolver o loop, a gente vai precisar de uma variável inteira .
Também vamos criar uma variável lógica chamada que será inicializada com o valor . Dessa forma, todo número é considerado primo até que se prove o contrário!
Então, vamos declarar essas variáveis no código:

Passo 3
Antes de escrever o laço precisamos receber o número do usuário. Usamos o para pedir o número e com o armazenamos o valor na variável correta.
![]()
Passo 4
Agora é a hora mais legal da questão. Vamos desenvolver um loop que testa se o número é ou não é primo.
Por definição, todo número primo é divisível por , então não faz sentido testar essa divisão. Da mesma forma, todo número primo é divisível por ele memo, e este é outra divisão que não precisamos testar.
Por isso, vamos inicializar a variável de iteração em , e vamos testar todos os números, de um em um, até menor do que . No código fica:
![]()
Pra testar se o número é primo vamos usar uma condição . Se o for divisível por então ele não é primo, e o valor lógico da variável deve ser mudado para .
Uma coisa que legal que podemos fazer é imprimir o valor atual de , e assim a gente vai saber qual foi o número que conseguiu dividir o .
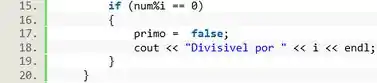
E é só isso. Temos um loop que testa se um determinado número é ou não é primo.
Passo 5
O loop está pronto. Mas ainda precisas imprimir a mensagem correta de se o número é ou não primo.
Pra isso podemos usar uma estrutura que confere a variável e imprime a mensagem adequada:
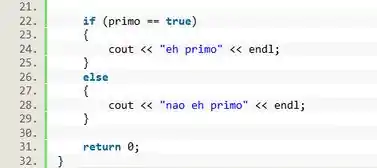
E é isso! Programa concluído.
Resposta
Exercício Resolvido #7
Adaptado de UFU – Faculdade de Computação – Programação Procedimental – Aula Prática: Estruturas de Repetição
Sejam as escalas Celsius e Fahrenheit para a representação de valores de temperaturas. Faça um programa para imprimir uma tabela com os valores de conversão de Celsius para Fahrenheit de -20ºC a +30ºC em intervalos de 5º:
Passo 1
Vamos lá, galerinha.
A questão pede pra gente desenvolver uma tabela com os valores de conversão entre Celsius e Fahrenheit.
Pra isso vamos precisar repetir o cálculo de conversão várias vezes seguidas, mas como somos espertos, vamos usar um laço for para efetuar essas repetições!
A nossa tabela começa com o valor de celsius em –20, e depois vai aumentando de 5 em 5 até chegar em +30. Então, vamos aproveitar esse comportamento da variável celsius e vamos usá-la como variável de iteração dentro do nosso laço for
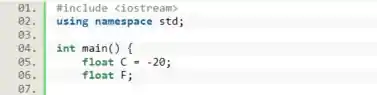
Como a estrutura do programa em mente, vamos pensar nas variáveis necessárias. Vamos precisar de uma variável float que armazena o valor de graus celsius, e podemos chamá-la simplesmente de C. E também vamos precisar de uma variável float para armazenar o resultado em Farhrenheit, vamos chamá-la de F.
Passo 2
Agora vamos desenvolver o loop.
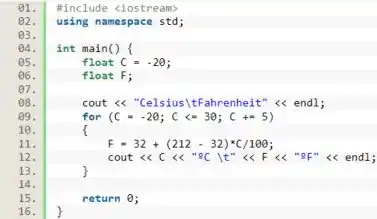
Pra deixar o programa bem bonito, vamos criar um cabeçalho pra nossa tabela. No lado esquerdo ficarão os valores em celsius, e do lado direito os valores em fahrenheit. Vamos usar o caractere especial “\t” para deixar tudo tabulado.
![]()
Vamos desenvolver um loop para gerar a tabela. O loop deve começar com o valor de C=-20 e deve crescer até C=30 de 5 em 5. Para fazer um valor crescer de 5 em 5 podemos utilizar o operador de atribuição +=
![]()
Dentro do loop vamos pegar o valor atual de C e usá-lo para calcular o valor atual de F:
![]()
Belezinha. Agora só precisamos imprimir os valores de celsius e fahrenheit

E com isso podemos fechar o loop e finalizar o programa.
Passo 3
Pra terminar a questão com chave de ouro, só falta testar o programa. Compilando e rodando a gente vai ter a seguinte saída:
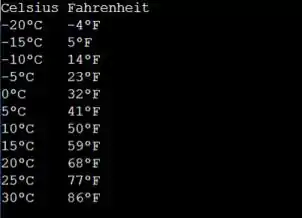
Resposta
Exercício Resolvido #8
Elaboração própria
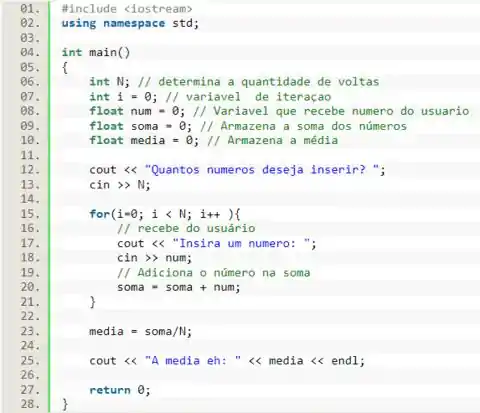
Receba N números do usuário e calcule a média aritmética.
Passo 1
Lets go, people!
Vamos precisar receber uma quantidade indefinida de valores do usuário. Mas a gente pode ser esperto e logo no início do programa perguntar pro usuário a quantidade de valores que ele quer inserir, e guarda isso numa variável N.
E depois que a gente souber a quantidade, a gente pode um laço em que uma variável chamada num recebe o número do usuário, e em seguida esse valor é adicionada uma variável chamada soma, que guarda a soma de todos os números já digitados. No loop seguinte, a variável
Beleza, assim a gente vai ter a soma dos valores na variável soma e vamos ter a quantidade de valores na variável N. Aí é só dividir o valor da soma pelo valor de N e poderemos guardar esse resultado numa variável media.
Massa demais. Com essa estrutura em mente, vamos declarar as variáveis que mencionamos acima. Ah, não se esqueça de que o loop vai precisar de uma variável de iteração, que vamos chamar de i

Passo 2
Agora precisamos saber quantas vezes o laço será repetido. Então vamos perguntar pro usuário quantos valores ele quer inserir.
Usando o cout vamos solicitar o valor e com o cin vamos atribuir o valor inserido a variável N
![]()
Passo 3
Beleza, com isso a gente pode desenvolver o loop.
Vamos precisar receber N valores. Então vamos criar um loop que começa em zero, e avança de um em um enquanto for menor do que N
![]()
A primeira atividade do laço vai ser receber um valor do usuário e atribuir este valor à variável num:
![]()
O valor recebido vai ser adicionado à variável soma. Pra isso usamos a expressão de atualização:

E assim finalizamos o nosso laço.
Passo 4
Agora é só a gente calcular a média. Nós já temos a soma, e temos a quantidade de valores. Então é só dividir:
![]()
E pra finalizar a questão, vamos imprimir o resultado utilizando o cout.

Resposta