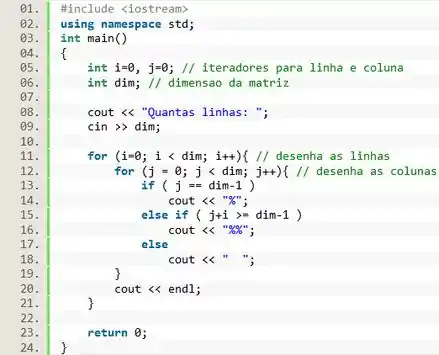
Loops infinitos, loops aninhados e os comandos break e continue
Produzido por Gustavo BarbosaTeoria
E aí galera, aqui é o Juan do Responde Aí, e hoje vamos aprofundar nossos conhecimentos sobre os loops.
Loop Infinito

Enquanto desenvolveu seus programas, talvez você já tenha caído sem querer em um loop infinito. Talvez tenha esquecido de incrementar a variável do loop. Ou talvez tenha feito uma condição de parada errada.
Só que as vezes, um loop infinito é exatamente o que queremos! Existem basicamente duas situações onde loops infinitos podem ser úteis:
- Quando o código deve rodar até o programa ser fechado ou o computador ser desligado. Esse é o caso quando programamos um Arduíno ou um microcontrolador. Também é o caso de servidores que estão sempre funcionando até serem desligados.
- Quando queremos que o código rode até que ele encontre algum “acontecimento específico”, e então siga pra próximas tarefas. Esse caso é comum quando queremos que o programa rode até que o usuário pressione algum botão específico.
E pra usar é bem simples: basta iniciar um loop com uma condição que é verdadeira para sempre! Porém, as formas mais comuns e mais adequadas de se fazer um loop infinito são:

Sacou? No primeiro exemplo, o laço não tem condição de parada nem de incremento, e por isso, vai ser executado indefinidamente. Já nos outros dois exemplos, as condições do e do serão sempre e por isso, esses loops vão durar para sempre.
Break: “que o pra sempre, sempre acaba”.
Talvez você já conheça o comando que é usado na função . Aqui a função é similar, o interrompe o loop que contém ele.
Exemplo: Crie um programa que multiplique todos os números impares que o usuário digitar. Se um número par for digitado, o loop deve ser interrompido.
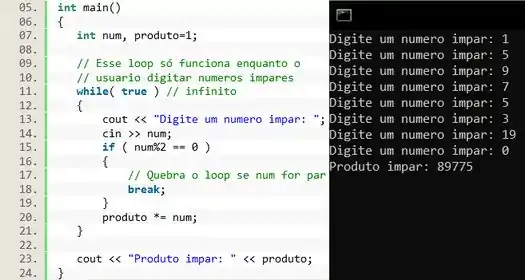
Na linha 11 a gente inicia o nosso loop infinito. Nas linhas 13 e 14 recebemos um número do usuário. Em seguida efetuamos um teste : se o número for par então usamos o comando para acabar com o loop, se for impar o é ignorado e efetuamos a multiplicação na linha 20.
Note uma coisa interessante, é possível criar um laço similar usando a expressão: . Quase sempre é possível escolher entre usar um loop finito ou um loop infinito com comando break. São duas possibilidades igualmente válidas!
Apesar da principal função do ser terminar loops infinitos, a gente também pode usá-lo para loops comuns se for necessário.
Continue a nadar para próxima iteração.
Outro comando usado para controlar loops é o . O que ele faz é: tudo que vem depois do é ignorado e a próxima iteração do loop é iniciada.
Ou em outras palavras, enquanto o interrompe o loop completamente, o apenas pula para a próxima iteração.
Exemplo: Faça um programa que multiplique todos os números impares que o usuário digitar, até que o produto seja maior do que . Se o número digitado for par ele não deve ser multiplicado.
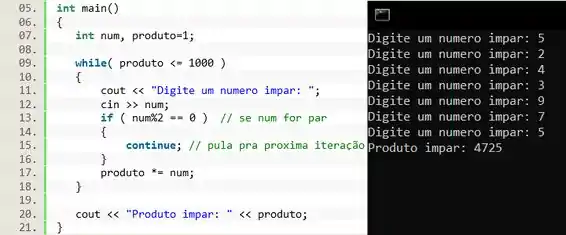
Esse programa é similar ao anterior. Nesse caso temos um loop com a condição de parada vinculada à variável na linha 09. Nas linhas 11 e 12 recebemos um valor do usuário. Fazemos um teste da linha 13: se o número for par o é acionado e voltamos pro início do laço para começar a próxima iteração. Se o número for ímpar, então realizamos o produto na linha 17.
O comando pode ser usado dentro de loops finitos ou infinitos, tudo só depende da necessidade!
Loops aninhados
À medida que seus programas ficarem mais complexos, você vai começar a sentir necessidade de usar loops dentro de outros loops. Chamamos essa prática de loops aninhados.

Vamos ver um exemplo e isso ficará mais claro.
Exemplo: Faça um programa que imprima uma matriz quadrada de tamanho qualquer. Represente o primeiro termo da primeira linha e primeira coluna como , o primeiro termo da segunda coluna como e assim por diante.
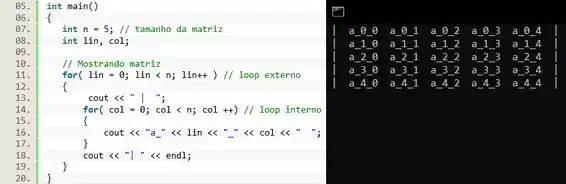
Primeiro vamos definir as nossas variáveis: define o tamanho da nossa matriz, dessa forma se a gente mudar o valor de , automaticamente a matriz irá se adaptar. Depois criamos duas variáveis: representa as linhas da matriz e as colunas.
Depois criamos um laço que vai escrever cada uma das linhas. E em cada linha vamos precisar escrever colunas e pra isso precisamos de um outro .
Loops aninhados são estruturas comuns e super úteis, mas aumentam muito o tempo de execução de um código. Então use com sabedoria, e evite usar mais do que dois loops aninhados, ou o desempenho do seu programa pode ser comprometido.

Agora pode surgir a dúvida de como os comandos e afetam os loops aninhados. Da uma olhada na próxima imagem. Eu circulei o comando e o loop que ele afeta.

E é isso, os comandos e afetam o loop mais interno em que eles estão dentro.
Não esquece de conferir os exercícios! Até mais 😉
Break: “que o pra sempre, sempre acaba”.
Loops aninhados
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Observe os dois códigos abaixo.
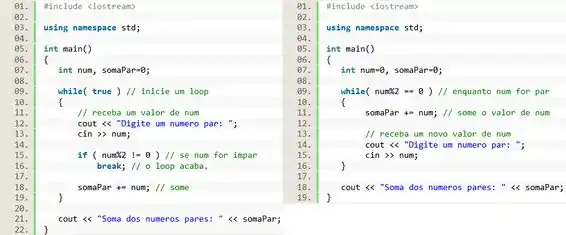
Do ponto de vista do usuário, existe alguma diferença? Explique
Passo 1
Vamos lá pessoal! Essa questão é legal.
Quando uma questão pede a comparação entre códigos, a melhor coisa que podemos fazer é executar os dois! E exatamente isso que vamos fazer.
Vamos executar o primeiro código:
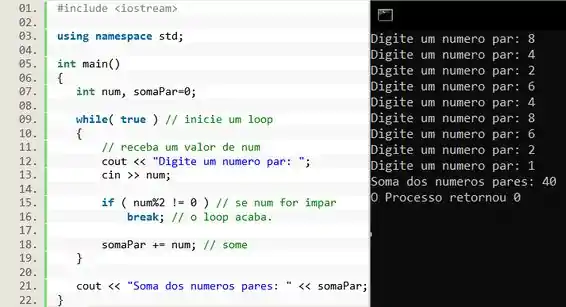
Nesse código temos um loop infinito que recebe um valor do usuário, em seguida testa se este valor é par. Caso seja impar o loop é interrompido, e caso seja par o loop continua e o número é somado ao resultado final.
Passo 2
Agora vamos executar o segundo código e ver o que acontece. Pra facilitar a comparação, vamos usar as mesmas entradas que usamos no programa anterior
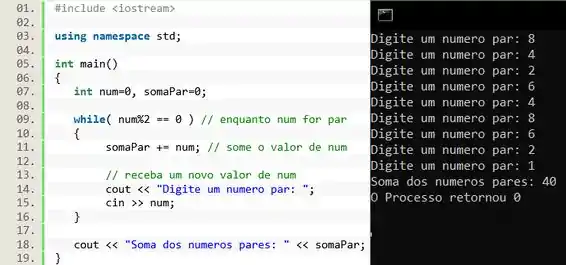
Nesse código o loop é iniciado com a condição de que só irá funcionar enquanto o número for par.
Note que pra isso ser possível, a variável tem que ser inicializada com o valor zero na linha 07. Pois se começar com um valor ímpar o loop não será iniciado. Se começar com um valor diferente de zero, a soma na linha 11 será prejudicada.
Passo 3
Certo, agora vamos comparar.
Do ponto de vista do usuário, não há nenhuma diferença entre os códigos. Os dois permitem que ele insira quantos números pares ele quiser. E caso digite um número ímpar então o programa acaba e é mostrada a soma de todos os números pares.
A diferença está apenas no código.
Isso mostra que um mesmo programa pode ser escrito de várias formar diferentes. As vezes usar um loop infinito com break pode ser mais ou menos prático. Quem decide isso é o gosto do programador.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração Própria
Faça um programa que some todos os números inteiros ímpares positivos que o usuário digitar. Se digitar um número negativo o programa é finalizado.
Passo 1
Vamos lá pessoal!
A questão quer que a gente receba vários números do usuário.
Se o usuário pode digitar vários números, então vai ser uma boa ideia usar um loop infinito. Mas primeiro vamos declarar nossas variáveis.
Vamos precisar de duas variáveis inteiras: guarda os números digitados pelo usuário, e guarda o valor dos números impares somados.
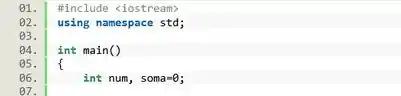
Passo 2
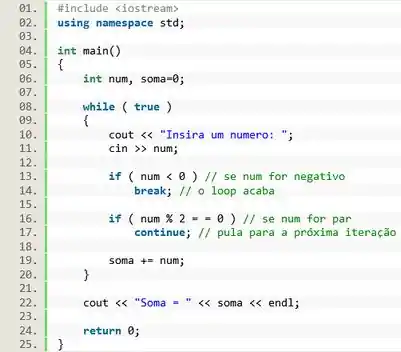
Agora vamos iniciar o nosso loop infinito. Pra isso vamos criar um laço com uma condição que será verdadeira para sempre:
![]()
Dentro do nosso loop vamos utilizar o vamos pedir um número pro usuário, e com vamos guardar o valor na variável
![]()
Na linha 13 e 14, a gente usa o comando vamos verificar se é negativo. Se for o caso, o comando é ativado e o loop é interrompido.
Já na linha 16 e 17, vamos considerar a segunda condição. Se o número digitado for par então não precisamos fazer nada. Vamos simplesmente pular para a próxima iteração utilizando o comando .
Mas se for impar as condições acima não são atendidas, e nesse caso podemos efetuar a operação de soma da linha 19.
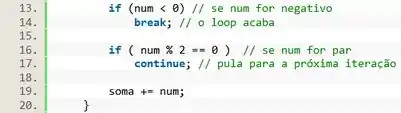
E com isso o nosso loop está feito!
Passo 3
Quando o loop for quebrado a gente tem que imprimir o valor da variável . Pra isso usamos o comando .

Resposta
Exercício Resolvido #3
Adaptado de UFRN – DCA800 – Exercício de Aprendizagem nº3 – Questão 6
Ler um número e imprima “1” se ele for primo e “0” se ele não for primo.
Passo 1
Oi pessoal, vamos lá resolver essa questão.
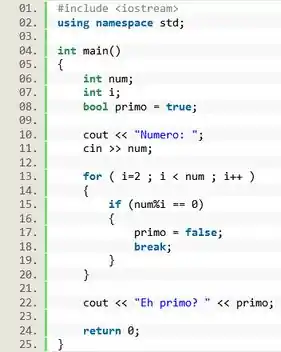
Vamos começar relembrando que um número primo é qualquer número inteiro e positivo que só seja divisível por 1 e por ele mesmo. Então, basta a gente criar um loop e testar todas as divisões possíveis. Se houver algum caso em que o resto da divisão seja zero, então o número não é primo.
Vamos começar declarando as variáveis. Vamos precisar de uma variável para conter o número inteiro digitado pelo usuário, chamada . Uma outra variável inteira chamada será a variável usada no nosso laço.
Também vamos criar uma variável lógica chamada que será inicializada com o valor . Dessa forma, todo número é considerado primo até que se prove o contrário!
Então, vamos declarar essas variáveis no código:
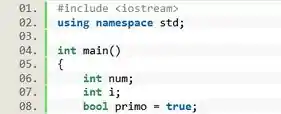
Passo 2
Antes de escrever o laço precisamos receber o número do usuário. Usamos o para pedir o número e com o armazenamos o valor na variável correta.
![]()
Passo 3
Agora vamos usar um laço para testar se o número é ou não primo.
Já sabemos que os números primos são divisíveis por um, então não faz sentido testar a divisão por, por isso vamos começar os testes partindo do . Da mesma forma, não faz sentido testar se o número é divisível por ele mesmo. Então, a expressão de teste do nosso laço vai ser:
Percebe que tem 3 informações aí (separadas por ponto e vírgula). Primeiro declaramos o valor inicial . Depois informamos até quando o loop deve continuar, ou seja, enquanto . Por fim, o termo significa que somamos 1 à variável , a cada iteração. Na interface, fica assim:
![]()
Agora dentro do loop! Pra testar se o número é primo vamos usar uma estrutura .
Se o for divisível por então ele não é primo, e o valor lógico da variável deve ser mudado para . Se isso acontecer uma vez, já é suficiente pra sabermos que o número não é primo. Nesse caso não será preciso continuar os testes, então usamos o comando para interromper o loop.
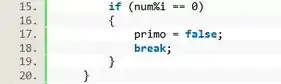
Passo 4
O nosso laço está finalizado! Agora é só imprimir a resposta pro usuário usando o comando para mostrar o valor contido na variável
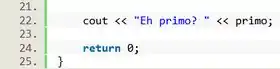
Resposta
Exercício Resolvido #4
Elaboração Própria
Receba dois números inteiros do usuário, um para base e outro para altura. Utilizando o símbolo imprima um quadrado com a base a altura especificada.
Exemplo:
Entrada:
Saída:
Passo 1
Essa questão é bacana!
Pra imprimir um quadrado como esse a gente vai precisar usar dois loops. Um pra gerar as linhas e um segundo pra gerar as colunas.
Mas antes, vamos declarar as variáveis. Vamos precisar de duas variáveis inteiras e pra receber os valores do usuário
E de mais outras duas variáveis inteiras para fazer um loop para as linhas e para o loop das colunas.
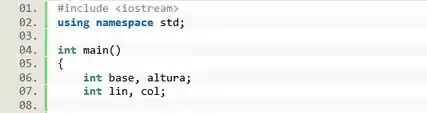
Passo 2
Agora vamos usar para pedir os valores pro usuário e com o vamos armazenar nas variáveis.

Passo 3
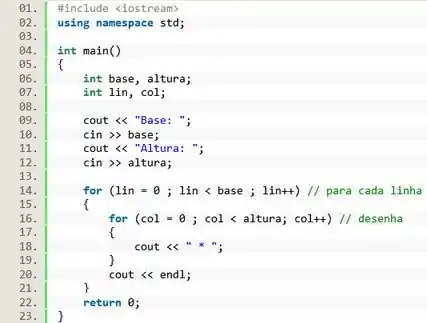
Primeiro construímos o loop das colunas. Começamos com e avançamos de um em um até .
![]()
E criamos um segundo loop. Ele deve começar em e se estender até . Em cada iteração vamos desenhar o símbolo . Note que eu usei espaços antes e depois do asterisco, para deixar o desenho mais bonito.

Com isso fechamos o laço interno.
Antes de fechar o laço externo vamos adicionar um salto de linha, para que a próxima iteração comece na linha seguinte.

E prontinho. Questão feita!
Passo 4
Agora só nos resta testar. Vamos rodar o código e escolher valores pra altura e base.
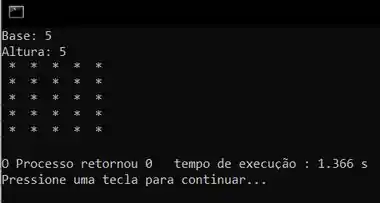
Massa demais né!
Resposta
Exercício Resolvido #5
Adaptado de UFRN – DCA800 – Exercício de Aprendizagem nº3 – Questão 6
Receba um número qualquer do usuário. Imprima todos os números primos existentes entre 0 e
Passo 1
Vamos lá pessoal. Essa questão é massa!
Pra encontrar um número primo basta a gente criar um loop e testar todas as divisões possíveis. Se o número for divisível apenas por 1 e por ele mesmo, então o número é primo.
Mas a gente precisa encontrar vários números primos! Então vamos criar outro loop, mais externo, pra poder repetir o processo de teste para todos os números.
Passo 2
Vamos começar declarando as variáveis. Vamos precisar de uma variável para conter o número inteiro digitado pelo usuário, chamada . E outras duas variáveis inteiras chamadas e serão usadas nos nossos loops.
Também vamos criar uma variável lógica chamada que será inicializada com o valor . Dessa forma, todo número é considerado primo até que se prove o contrário!
Então, vamos declarar essas variáveis no código:

Passo 3
Antes de escrever o laço precisamos receber o número do usuário. Usamos o para pedir o número e, com o , armazenamos o valor na variável correta.

Passo 4
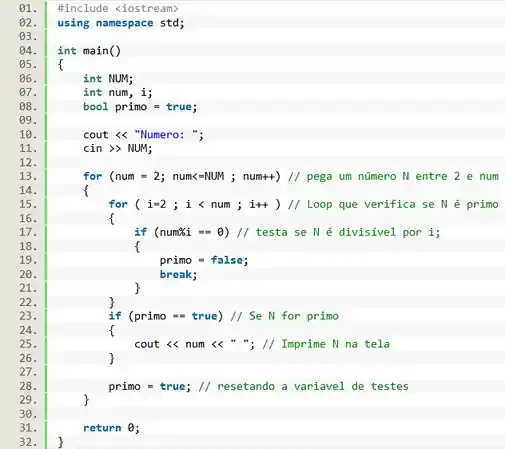
Agora vamos criar nosso primeiro loop usando o . Nesse loop vamos testar todos os números de 2 até , para descobrir quais são primos. Por definição não é primo, então o laço deve começar em . Então, a cada iteração, a variável assume um desses valores (de 2 até ) e é testada. Dentro do parênteses ali à direita do , é indicado o valor inicial da variável , o ponto de parada do loop e o comando que adiciona 1 à variável a cada iteração. Esses 2 informações devem ficar separadas por ponto e vírgula.
![]()
Agora vamos criar um segundo loop, para verificar se o número é ou não é primo. Pra isso iniciamos nosso laço em , pois não faz sentido testar a divisão por . E esse laço ira ser incrementado de um em um até , pois não faz sentido testar a divisão por si mesmo. Um número não primo é divisível por outros números além de 1 e ele mesmo, por isso testamos entre 2 e .

Pra testar se é divisível por vamos usar uma estrutura . Se o for divisível por então ele não é primo, e o valor lógico da variável deve ser mudado para e nesse caso não será preciso continuar os testes, então usamos o comando para interromper o loop interno.

Uma vez que o loop interno é concluído, ou seja, já sabemos se um determinado número é primo, precisamos imprimir essa mensagem. Precisamos imprimir todos os números que são primos. Então utilizamos outro comando que, caso o número testado seja primo, então vamos imprimir o número seguido de um espaço em branco. Esse fica dentro do loop externo, ou seja, logo que verificamos que um número é primo, já imprimimos seu valor, antes de analisar o próximo. E como não usamos o comando (que pula linha), todos os números primos são impressos na mesma linha, por isso é necessário prever um espaço.

Depois de imprimir um número primo, é hora de analisar o próximo. Mas antes, ainda dentro do loop externo, vamos precisar resetar a variável pro valor . Isso garante que a próxima iteração do laço ira funcionar corretamente.

Passo 5
Vamos dar uma olhada no resultado final pra testar. Vamos rodar o programa e inserir um valor qualquer. Eu vou usar
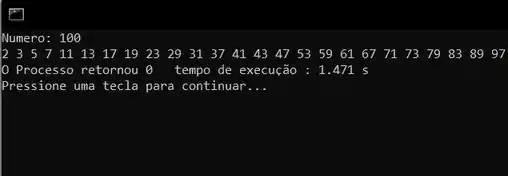
Resposta
Exercício Resolvido #6
Adaptado de UFMA
Desenhe um triângulo retângulo utilizando o caractere . O usuário deve inserir a quantidade de linhas do triângulo:
Exemplo com 5 linhas:
Passo 1
E aí galerinha. Essa é uma clássica questão de desenho usando caracteres, e costuma cair em provas.
O que vamos fazer aqui é criar dois loops aninhados, onde um é responsável por desenhar a quantidade de e o outro é responsável por realizar os saltos de linha.
Então vamos começar criando o cabeçalho do programa e declarando as variáveis. Como teremos dois loops, vamos precisar de duas variáveis de iteração e . E para receber a quantidade de linhas do triângulo vamos criar uma variável de dimensão chamada .
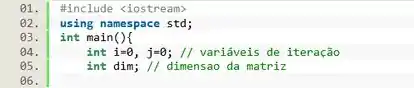
Passo 2
Em seguida vamos receber a dimensão do usuário. Com o e vamos solicitar a dimensão do triângulo e armazenar na variável .

Passo 3
E agora vamos lá pros nossos loops.
Primeiro vamos criar o loop externo, ele vai iniciar na linha (primeira linha) e vai aumentando de um em um até chegar na última linha correspondente a dimensão.
![]()
Em seguida vamos criar o loop interno. Ele também deve iniciar no (primeira coluna) e aumentar de um em um, porém perceba que o número de desenhados depende da linha. Na primeira linha é desenhado um , na segunda linha são desenhados dois , e assim por diante.
Ou seja, o ponto de parada do segundo loop depende do valor de . Então vamos fazer o loop interno iniciar em , avançar de um em um, mas parar quando atingir um valor igual ao valor das linhas:
![]()
E agora é só imprimir o símbolo na tela com o , e fechar o loop interno
![]()
Antes de fechar o loop externo a gente executa um salto de linha:
![]()
E finalizamos o programa:
![]()
Passo 4
E pra terminar, vamos testar o código:
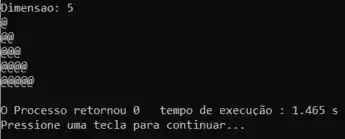
E deu tudo certo com o nosso programinha.
Resposta
Exercício Resolvido #7
Elaboração Própria
Faça um programa que receba um número do usuário e desenhe uma matriz identidade com estas dimensões.
Se o usuário inserir o número a saída deve ser:

Passo 1
E aí galerinha, vamos lá pro exercício. A questão quer que a gente receba um valor do usuário e imprima uma matriz identidade.
Antes de mais nada, a gente precisa lembrar que uma matriz identidade é uma matriz compostas por 1 na diagonal principal, e por 0 em todas as outras posições. De forma matemática, podemos representar assim:
onde o é a linha e o é a coluna.
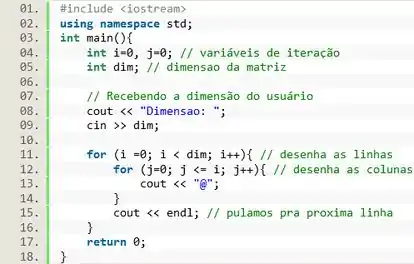
Uma forma de desenhar uma matriz no C++ é utilizando dois loops aninhados: um loop imprime todos os valores de uma linha, quando esse loop chegar ao fim a gente salta uma linha e o loop começa de novo. Ou seja, temos um loop dentro de outro.
Então, pra começar vamos declarar as variáveis e que serão usadas nos nossos loops, e também a variável que vai receber a dimensão da matriz inserida pelo usuário.
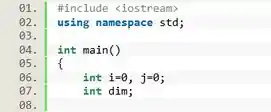
Passo 2
O passo seguinte é utilizar os objetos e para solicitar que o usuário insira a dimensão da matriz identidade.
![]()
Passo 3
Agora vamos pro coração da questão.
Primeiro a gente cria um loop externo, que comece a contar a partir do zero, e aumente a contagem de um em um, até o tamanho da dimensão da matriz.
![]()
Um loop interno atua de maneira semelhante, contando do zero até a dimensão da matriz de um em um
![]()
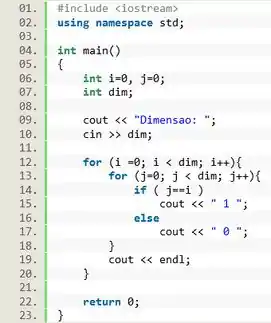
Para desenhar uma matriz identidade precisamos imprimir o valor na diagonal principal, então vamos utilizar uma estrutura para identificar os momentos e que o valor da linha e da coluna são iguais. Se as e forem iguais devemos imprimir o valor “ 1 ”, se forem diferentes imprimimos “ 0 ”.
Detalhe, coloque um espaço dentro das aspas, pois se não tiver um espaço os números da matriz ficarão grudados um no outro.
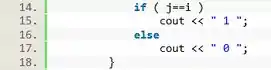
Com isso podemos fechar o loop interno.
Já o loop externo terá que efetuar a operação de saltar de linha. Assim, na próxima iteração do loop interno, ele irá imprimir na próxima linha.
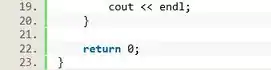
Passo 4
Agora vamos testar o código pra saber se deu tudo certo:
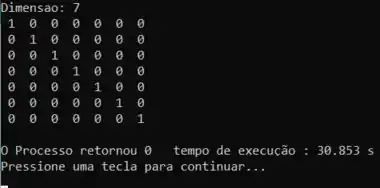
E prontinho, o programa está rodando lindão!
Resposta
Exercício Resolvido #8
Adaptado de UTFPR – Curitiba – prof. Leonelo Almeida – IF61A/IF71A Computação 1
Faça um programa que desenhe na tela um triângulo utilizando somente o caractere . O usuário deve escolher a quantidade de linhas que formam o triângulo.
Exemplo, para 6 linhas:

Passo 1
Vamos lá pessoal.
A questão pede pra gente desenhar um triângulo usando o símbolo . A maior dificuldade está no fato de que esse triângulo possui a altura alinha à direita. Isso quer dizer que vamos precisar preencher vários caracteres de espaço em branco para empurrar cada um dos para o lugar certo.
Mas primeiro vamos entender como esse triângulo é formado. Note que a primeira linha possui apenas um símbolo de , a segunda linha tem três, a terceira tem cinco... ou seja, vão aumentando de dois em dois.
Vamos usar o exemplo de 6 linhas que foi dado pela questão. A gente pode imaginar esse triângulo como uma matriz, e dividir a quantidade de símbolos entre as células da matriz
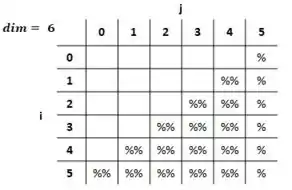
Por enquanto, não vamos nos preocupar em quantos temos em cada célula, vamos só pesar: “O que faz uma célula ser preenchida ou ficar vazia”?
Lembrando da álgebra linear, a gente pode notar uma coisa: na diagonal secundária, a soma do é sempre constante. Não entendeu? Então olha só essa imagem:
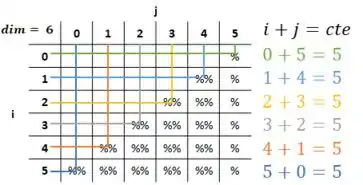
Note que o “” que obtivemos é igual a “”... e olha que show de bola, é o valor da dimensão da matriz!
E mais uma coisa interessante sobre matrizes quadradas é que esse fenômeno acontece em todas as diagonais paralelas a diagonal secundária! Olha aí em baixo uma matriz em que cada elemento é preenchido com o valor de
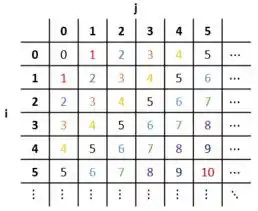
Passo 2
Então, vamos observar que:
- O valor das diagonais é constante.
- O valor da diagonal secundária é igual a
Então, pra desenhar esse triângulo, o que precisamos fazer é preencher todas as células em que seja igual ou maior a . Podemos determinar isso com uma instrução
Mas um detalhe, a última coluna é preenchida com apenas um único . Note que a posição da última coluna é igual a . Então, quando devemos escrever somente um .
Porém, como fazemos pra acessar todas as células de uma matriz? Pra isso usamos dois loops aninhados. O loop externo é responsável pelas linhas, e o loop interno é responsável pelas colunas.
Aplicando a lógica dos loops aninhados sobre a estrutura anterior vamos ter o seguinte algoritmo:
Que vai imprimir os de acordo com a seguinte lógica:
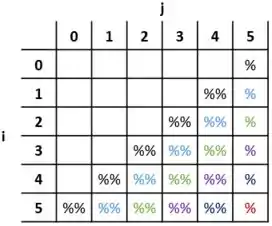
Passo 3
Vamos olhar agora pro algoritmo que desenvolvemos e vamos implementá-lo em linguagem C++. Pra começar escrevemos o cabeçalho e declaramos três variáveis: e para representar as linhas e colunas da nossa matriz, e a variável que determina a dimensão da matriz
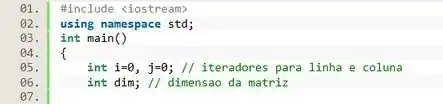
Em seguida vamos receber o valor de do usuário. Pra isso vamos usar os comandos e :
![]()
Passo 4
Show, agora vamos implementar o algoritmo de fato:
Primeiro criamos um aninhamento de loops, para podermos iterar em cima da nossa matriz:
![]()
E dentro desses loops, vamos implementar a estrutura :
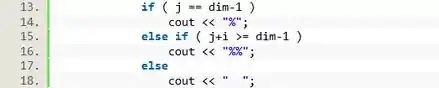
E com isso podemos fechar o loop interno e adicionar um salto de linha, depois fechamos o último loop e finalizamos o programa:
Passo 5
E claro, antes de terminar precisamos testar o programa:
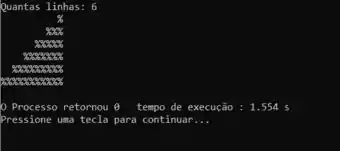
E prontinho! Finalizamos essa questão super da hora!
Resposta