Expressões e precedência
Produzido por Gustavo BarbosaTeoria
E aí, aqui é o Juan do Responde Aí. E hoje vamos falar de expressões matemáticas e a precedência dos operadores no C++
Evitando confusões.
Talvez você já tenha visto por aí alguns memes de matemática tipo esse:

Geralmente quem faz esse tipo de meme escreve uma expressão matemática confusa de propósito! No exemplo acima você pode resolver a questão de duas formas
Assim:
Ou assim:
Até calculadoras ficam confusas com esse tipo de conta. Olha esse exemplo com a expressão

Existem muitas formas de escrever expressões matemáticas confusas que nos levam a erros. Pra evitar esse tipo de erros devemos sempre escrever expressões usando corretamente as regras de precedência e associatividade.
Expressões em C++
Como você escreveria a seguinte expressão no C++?
Se eu escrever dessa forma, estaria correto?
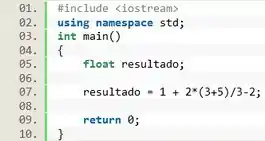
O código acima está muito errado! Na matemática as operações ocorrem em uma ordem: primeiro parêntesis, depois multiplicação e divisão, e só depois a soma e subtração.
A melhor forma de escrever a expressão é usando os parêntesis, pra forçar a expressão a seguir a ordem que a gente quer! Se a gente escrever dessa outra forma, estará bem melhor:
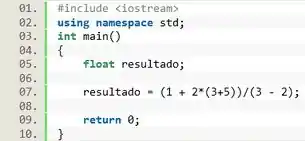
Essa ordem das operações é chamada de precedência, e é isso que vamos estudar agora:
Precedência de operadores da linguagem C++
No vocabulário dos programadores, a palavra precedência se refere a ordem que as operações são executadas. Já a associatividade é a ordem que os operadores começam a ser resolvidos, que pode ser da direita pra esquerda ou da esquerda pra direita.
Ficou confuso? Então olha esse exemplo: como resolvemos ? Primeiro resolvemos a multiplicação, e depois resolvemos a soma: . Isso é um exemplo de precedência! A multiplicação vem primeiro porque ela tem uma precedência maior.
Agora outro exemplo. Se a gente tiver uma variável , como o C++ resolve a expressão ? Bem primeiro ele resolve a expressão na direita , e depois ele guarda o valor na variável da esquerda. Isso é um exemplo de associatividade, onde o operador de atribuição () é resolvido da direita para a esquerda!
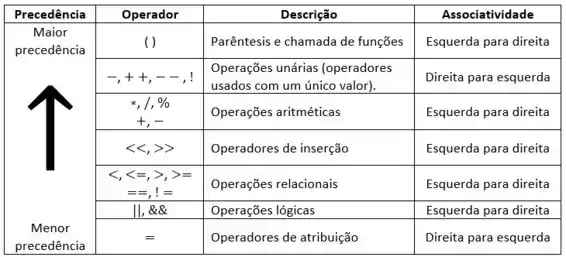
De maneira geral, a precedência e associatividade do C++ funcionam igual a matemática tradicional. Mas se tiver dúvida, dá uma olhada nessa tabela:
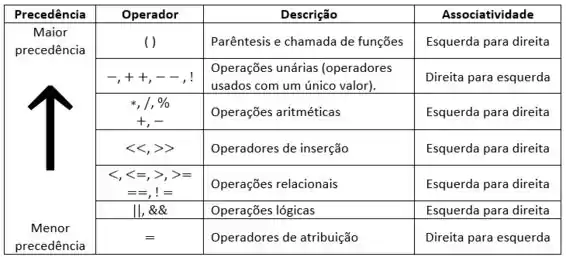
Com a maior precedência estão os parêntesis. Na sequência os operadores unários, depois aritméticos, e em seguida os de inserção, relacionais e lógicos e por último os operadores de atribuição.
Ah, só um detalhe, o símbolo pode ser operador unário de negativo, que transforma o positivo (um) no negativo (menos um), por exemplo. Mas também pode ser o operador aritmético de subtração.
Bom, e a teoria é essa. Pra fixar bem, o melhor é fazer uns exemplos.
Exemplo 1: Como o C++ resolveria a operação ?
Pelas regras de precedência, primeiro resolve a divisão e a multiplicação, e depois resolvemos a soma:
Olha o resultado no código:
![]()
Exemplo 2: Como o C++ resolve a expressão ?
Aplicando as regras de precedência primeiro resolve o parêntesis:
Depois a multiplicação e o módulo
E por fim resolvemos a soma
No C++ fica assim:
![]()
Exemplo 3: Como o C++ resolveria a expressão ?
Essa é aquela expressão confusa lá do começo. Pra começar, vamos resolver os parêntesis
Certo, mas e agora? Se a multiplicação e divisão têm a mesma precedência, qual delas deve ser resolvida primeiro? Nesse caso olhamos pra regra de associatividade, e resolvemos a expressão da esquerda pra direita.
Primeiro a divisão:
Depois a multiplicação:
E olha só ela no código:
![]()
Exemplo 4: Qual o resultado da expressão
Essa expressão é um pouco grande. Mas fazendo com calma não tem erro. Primeiro vamos resolver os parêntesis internos:
Agora os parêntesis externos:
Depois resolvemos a divisão:
Resolvemos as somas:
E por último, resolvendo a operação relacional. Sabemos que é maior do que . Logo o resultado da expressão relacional é verdadeiro, que no C++ é representado pelo número
Olha só essa expressão no C++
![]()
Criando boas expressões matemáticas com C++
Agora que você acabou de ver as regras talvez tenha achado um pouco confuso, ou tenha achado que é coisa demais. Mas com a prática você se acostuma.
Mas fica tranquilo, vou te dar umas dicas pra não ter risco de errar
- Na dúvida, usa os parêntesis. Você pode usar e abusar deles pra colocar as expressões na ordem que você quiser.
- Separe uma expressão grande em expressões menores
- Evite colocar incrementos e decrementos dentro das expressões. Eles podem deixar o código difícil de ler.
E por hoje é isso. Agora vamos ver uns exercícios de fixação.
Precedência de operadores da linguagem C++
Criando boas expressões matemáticas com C++
Exercícios Resolvidos
Exercício Resolvido #1
Livro: C++ Absoluto – Savitch – 2014 – Capítulo 1 – Projeto de Programação 2
Um laboratório de pesquisas governamental conclui que um adoçante artificial comumente usados em refrigerantes dietéticos causa a morte de ratos de laboratório. Um amigo seu está desesperado para perder peso e não consegue deixar de tomar refrigerantes. Seu amigo quer saber quanto refrigerante dietético é possível tomar sem morrer. Escreva um programa para dar essa resposta. Os dados de entrada serão a quantidade de adoçante artificial necessária para matar um rato, o peso do rato e o peso da pessoa em dieta. Para garantir a segurança do seu amigo, faça com que o programa requisite o peso com o qual ele deseja ficar, em vez do peso atual. Assuma que o refrigerante dietético contém um décimo de 1% de adoçante artificial. Utilize uma declaração de variável com o modificador const para dar um nome a esta fração. Você pode querer expressar a porcentagem como o valor double 0.001.
Passo 1
Vamos lá galera, essa é uma questão de proporção.
Pra começo de conversa, a questão da uma informação importante o refrigerante dietético contém um décimo de 1% de adoçante, então vamos guardar essa informação em uma constante do tipo chamada
A questão nos diz quais são as entradas do programa então vamos criar variáveis para guardar cada uma: A primeira é a quantidade de adoçante capaz de matar um ratinho, criamos a variável . A segunda é o peso do rato, vamos chamar de . E a terceira é o peso que o amigo quer atingir, com o nome . O tipo dessas variáveis deve ser , para permitir valores reais com alta precisão.
Agora, temos que levar em consideração quais serão as saídas do programa. A primeira saída é a quantidade máxima de refrigerante dietético, vamos chamar de . Porém, pra facilitar os cálculos, vamos criar também uma variável intermediária chamada para guardar a quantidade máxima de adoçante.
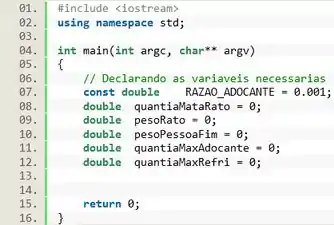
Passo 2
Show! Agora vamos usar o cin para receber os valores do usuário. Não esqueça de usar o cout para imprimir uma mensagem pro usuário.
Outro detalhe, pra facilitar nossas contas vamos pedir todos os pesos em gramas.
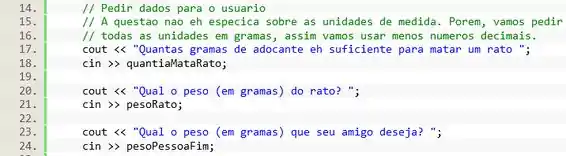
Passo 3
Agora é hora de calcular nossos resultados. Pra calcular a quantidade máxima de adoçante vamos usar a expressão:
E pra calcular a quantidade máxima de refrigerante vamos usar essa outra expressão:
Essa é a melhor forma de fazer pois com duas contas simples teremos menos chance de errar.
Vamos colocar isso no nosso código:

Passo 4
E pra finalizar a questão vamos usar o cout para imprimir duas mensagens que informem a quantidade máxima de adoçante e de refrigerante que podem ser consumidos.

E xablau! Questão resolvida!
Resposta
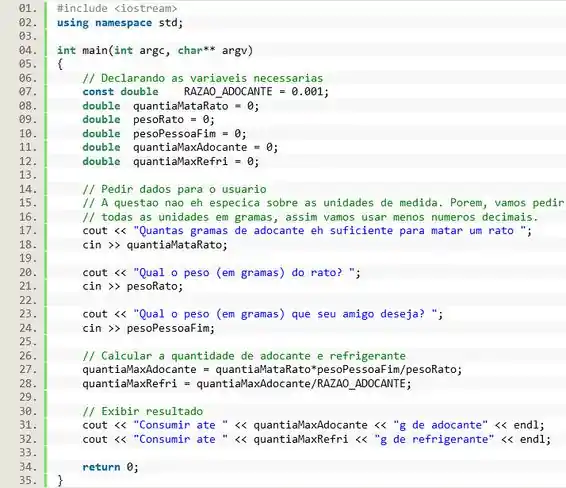
Exercício Resolvido #2
Lista de Exercícios UFRN – DCA800
Calcule a quantidade dinheiro gasto por um fumante. Dados: o número de anos que ele fuma, o nº de cigarros fumados por dia e o preço de uma carteira com 20 cigarros.
Passo 1
Vamos analisar quais são as entradas e saídas deste programa, e vamos decidir o tipo e o nome pras variáveis.
Entradas:
- Quantos anos o usuário fuma: vamos usar uma variável chamada , possibilitando que o usuário fume “um ano e meio” por exemplo.
- A quantidade de cigarros pode ser do tipo chamada , pois é incomum fumar “meio cigarro”
- O preço da carteira pode ser do tipo chamada , pois precisamos de apenas duas casas decimais para inserir dinheiro.
Saídas: A quantidade de dinheiro gasto, pode ser do tipo chamada .
Além disso, a questão informa a quantidade de cigarros em uma carteira, vamos guardar numa variável chamada
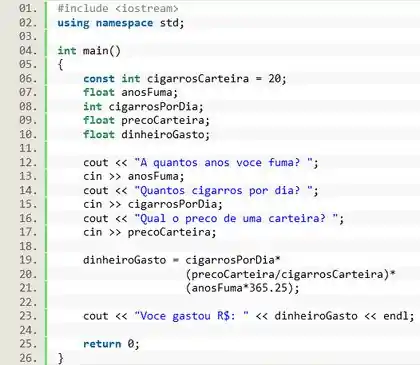
Então vamos criar as variáveis e constantes:
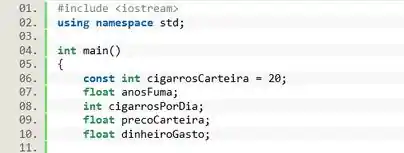
Passo 2
Agora vamos pedir as entradas pro usuário. Pra isso a gente usa a função para enviar uma mensagem pro usuário, e com a função a gente recebe os valores que o usuário digitar:
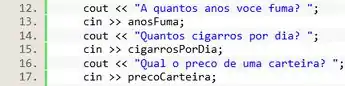
Passo 3
E agora é hora da matemática!
O preço de um cigarro é o preço da carteira, dividido pela quantidade de cigarros numa carteira:
A quantidade total de dias fumando, considerando anos bissextos, é:
Então, o total gasto com cigarros é:
Vamos colocar isso no C++:

A expressão ficou muito grande. Então basta pular pra próxima linha e continuar a conta normalmente. Lembre-se: pro C++ uma linha de código só acaba quando ele encontra o ponto e vírgula.
Passo 4
Pra finalizar a questão, é só a gente imprimir o resultado na tela, e pra isso usamos o :

Resposta
Exercício Resolvido #3
Elaboração propria
Uma equação do segundo grau é do tipo
Receba os valores de , , , e um valor qualquer para , e calcule o valor de .
Passo 1
Vamos lá:
As entradas desse programa são os valores de , , e . Essas variáveis podem ser quaisquer valores reais, então vamos usar o tipo .
O resultado é , que também pode assumir qualquer valor real, então vamos usar o tipo também.
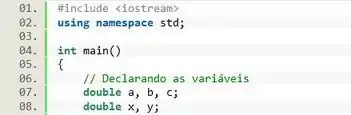
Passo 2
Agora, usando o vamos receber os valores do usuário. Com o imprimimos mensagem pra guiar o usuário:

Passo 3
Agora vamos fazer as contas. É só aplicar a equação descrita na questão.
Pra conseguir o valor de vamos fazer . Depois é so colocar . Como as multiplicações são calculadas primeiro, nem precisamos nos preocupar em usar parêntesis.
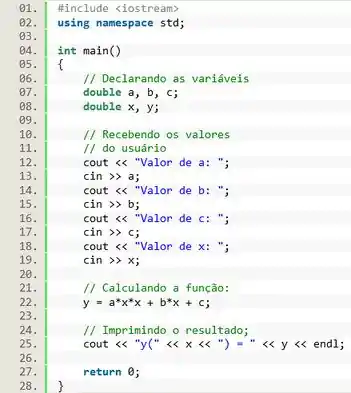
No código fica assim:
![]()
Passo 4
E pra finalizar, vamos imprimir o resultado na tela.
Usando o de uma maneira esperta, a gente pode fazer o C++ imprimir o valor de entre parêntesis, saca só:
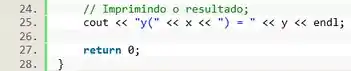
E questão finalizada.
Resposta
Exercício Resolvido #4
Elaboração própria
João escreveu uma expressão onde quando , e quando . A expressão ficou dessa forma:
Sabendo que e são variáveis do tipo double responda:
Demonstre a ordem que as expressões serão executadas.
Mostre que quando .
Mostre que quando .
Passo 1
Vamos lá. Essa é uma questão de precedência e associatividade. Então vamos tirar um tempinho pra lembrar da nossa tabela:
Passo 2
A gente sempre deve começar pelos parêntesis mais internos. Nesse caso é a expressão destacada em vermelho:
![]()
Agora temos 4 parêntesis externos. Todos tem a mesma precedência, mas pela regra de associatividade devemos analisá-los da esquerda para direita
![]()
Depois que os parêntesis estão resolvidos, temos que calcular as multiplicações. Temos duas multiplicações, então, pelas regras de associatividade, devemos analisar da esquerda pra direita.
![]()
Depois é calculada a soma:
![]()
E por fim o valor resultado é guardado na variável :
![]()
Passo 3
Belezinha. Agora vem comigo que vamos colocar essa sequência de passos em prática
Primeiro, onde tiver vamos substituir por :
Em seguida, vamos resolvemos o parêntese mais interno:
Na sequência, resolvemos os parêntesis externos
A gente sabe que e , vamos substituir:
Agora vamos resolver as multiplicações:
E por fim a soma:
Passo 4
Legal né?!
Vamos fazer o mesmo passo a passo, mas para
Primeiro resolvemos o parêntese mais interno:
Agora os parêntesis externos
Sabemos que e , então vamos substituir:
Agora vamos resolver as multiplicações:
E por fim a soma:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Livro: C++ Absoluto – Savitch – 2014 – Capítulo 1 – Projeto de Programação 3
Os trabalhadores de uma empresa em particular receberam um aumento de 7,6% retroativo a seis meses. Escreva um programa que tome o salário anual anterior de um empregado como entrada e apresente como saída a quantidade de pagamento retroativo devido ao empregado, o novo salário anual e o novo salário mensal. Utilize uma declaração de variável com o modificador const para expressar o aumento de pagamento.
Passo 1
Pra começar, vamos analisar o que a questão quer e o que ela nos dá:
A entrada de dados é o salário antigo, vamos criar uma variável chamada
As saídas do programa são: o salário anual, o salário mensal e o pagamento retroativo. Vamos criar então três variáveis do tipo chamadas , , e .
A questão oferece como dado o valor percentual do aumento semestral, que vamos declarar como , como é um valor fixo de alta precisão será uma .
Ah, a questão tem uma pegadinha: os valores serão calculados com base no salário anual, porém, a resposta do programa é para um semestre.
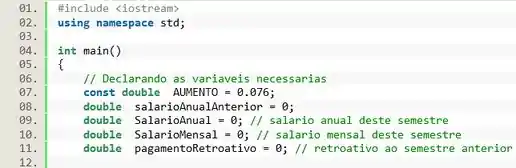
Passo 2
Usando o a gente imprime uma mensagem pro usuário e com o vamos receber o valor do salário antigo:

Passo 3
Agora vamos efetuar os cálculos.
O novo salário é um aumento percentual sobre o salário antigo. Então podemos dizer:
Organizando essa expressão, podemos simplificar da seguinte forma:
Escrevendo no C++:
![]()
Agora que temos o salário anual, basta dividir por 12 para ter o salário mensal:
![]()
Já sabemos o novo salário do empregado. Mas ele trabalhou 6 meses recebendo o salário antigo, então ele precisa receber a diferença que falta.
Para calcular o quanto a empresa deve, vamos subtrair o novo salário anual do salário anual antigo. Depois é só dividir por dois para ter a diferença para 6 meses.
![]()
Passo 4
Agora é so a gente imprimir as informações na tela utilizando o cout:
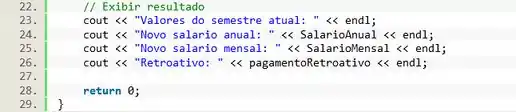
Resposta
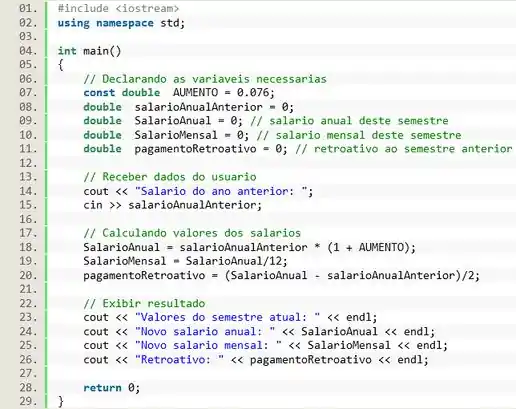
Exercício Resolvido #6
Elaboração própria
Para saber a equação de uma reta precisamos ter um ponto inicial e um vetor diretor . Com o ponto inicial e o vetor diretor, a equação da reta é dada por:
Onde é uma variável de parametrização.
Conhecendo o ponto e o vetor é possível calcular a posição da reta para qualquer valor de .
Receba do usuário o ponto , o vetor e um valor de , e calcule a imprima a .
Passo 1
E aí pessoal. Aqui é o Juan do Responde Aí, e vamos lá resolver esse exercício.
A questão tem um enunciado bem grande, mas é só porque ela explica pra gente como calcular a equação de uma reta. Na prática, só o que a gente precisa fazer é receber as componentes do ponto, do vetor e o valor de e calcular a reta usando o sistema de equações.
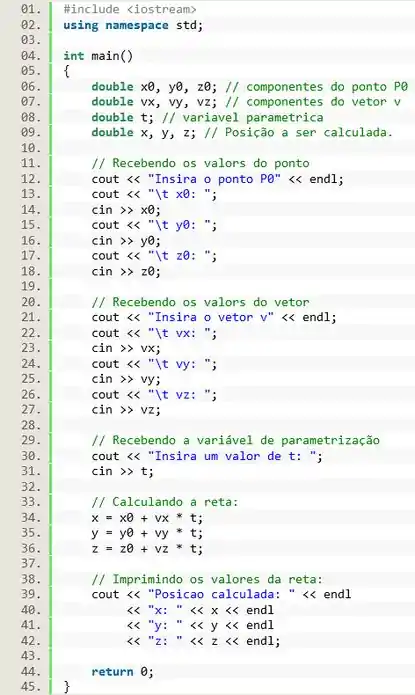
Mas pra começar, a gente precisa escrever o cabeçalho do programa:
![]()
Também precisamos declarar as variáveis do programa. O ponto é composto por três números (suas componentes). Então para receber esse ponto vamos precisar de três variáveis, uma pra cada componente: e , todas do tipo para termos alta precisão de cálculo.
![]()
Seguindo o mesmo princípio, vamos declarar o vetor , que também é composto por outros três números: , e . Elas também serão do tipo
![]()
Já a variável é um valor escalar. Então só precisamos receber o valor de normalmente:
![]()
Certo, já temos tudo que precisamos para calcular a reta! Porém precisaremos de variáveis para guardar esses resultados. Então vamos criar as variáveis , e para armazenar os resultados. Note que essas variáveis devem ser do tipo , pois todas as demais variáveis da equação são deste tipo também:
![]()
Passo 2
Show de bola! Temos as variáveis todas declaradas, então precisamos preencher as variáveis com os valores do usuário. Para isso vamos usar o para solicitar os valores, e o para armazenar cada valor na variável adequada
Primeiro, na linha 12, vamos exibir uma mensagem informado qual item vamos receber. Eu vou querer receber primeiro o ponto . Em seguida, na linha 13, vou informar para o usuário que quero receber a componente . Note que coloquei uma tabulação para facilitar a visualização. E na linha 14 usamos o comando para guardar o valor digitado na variável . E vamos repetir o mesmo processo nas linhas 15 a 19 para receber as demais componentes do ponto :
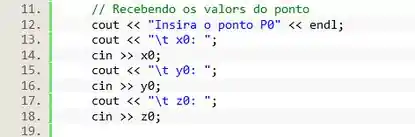
Seguindo a mesma lógica, vamos receber também os valores do vetor e armazenar nas variáveis , e .

E também vamos receber um valor para a variável paramétrica :

Belezinha!
Passo 3
Ok, agora que temos todos os valores, podemos calcular o valor da reta. Pra isso, vamos precisar montar as seguintes equações:
Vamos usar o operador de multiplicação () e o operador de adição () para escrever a equação e com o operador de atribuição () guardamos na variável adequada.
A precedência maior é do operador de multiplicação, depois do de soma e por último do operador de atribuição. Então, nesse caso não vamos precisar utilizar parêntesis:
![]()
E fazemos o mesmo para calcular e :
![]()
Passo 4
Agora a questão ta quase concluída. Só precisamos exibir o resultado, e pra isso vamos usar o .
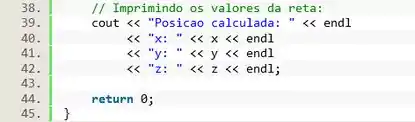
Passo 5
Para testar se o programa funciona direitinho, vamos rodar ele com os seguintes valores
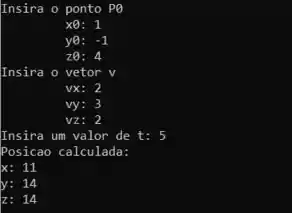
E rodou liso que nem manteiga! Deu tudo certo, questão concluída!
Resposta
Exercício Resolvido #7
Lista de Exercícios UFRN – DCA800
Leia a razão de uma PA (Progressão Aritmética) e o seu primeiro e último termos e informe a soma dos elementos dessa PA.
Passo 1
Vamos nessa, galerinha!
Pra começo de conversa, vamos lembrar o que para calcular a soma dos elementos de uma P.A a gente precisa saber três coisas: o primeiro termo , o último termo , e quantidade de termos da P.A.
Mas nessa questão o usuário vai inserir a razão da P.A. e não vai inserir a quantidade de termos, e agora? 🤷♂️🤷♀️
Sem pânico! A gente pode calcular a quantidade de termos da seguinte forma:
Massa né! Então vamos por
Passo 2
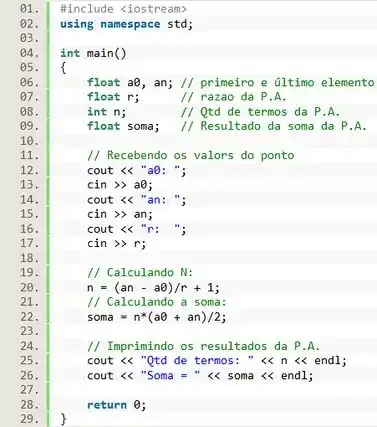
Pra começar o nosso programa, vamos escrever o cabeçalho do código:
![]()
E vamos determinar as nossas variáveis. De cara vamos precisar dos elementos inicial e final da progressão. Como esses elementos podem ser quaisquer valores reais, vamos declará-los como :
![]()
Em seguida vamos declarar uma variável para armazenar a razão da P.A., que também pode assumir qualquer valor real:
![]()
Para calcular a soma, primeiro teremos que calcular a quantidade de elementos da progressão. A quantidade de termos sempre será um valor do tipo inteiro! Então vamos declarar uma variável do tipo
![]()
E por fim, vamos precisar de uma variável pra armazenar o resultado da soma. Esse valor pode ser qualquer valor real, então vamos declarar mais uma variável do tipo
![]()
Passo 3
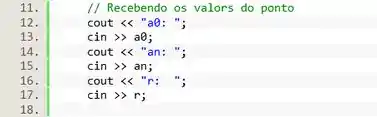
Show! Com as variáveis declaradas já podemos receber os valores do usuário. Vamos usar o e o para receber os valores de , e
Com o solicitamos um valor do usuário, e logo em seguida usamos o para armazenar na variável adequada. Isso é feito três vezes, para receber as três variáveis:
Passo 4
Agora é hora da MATEMÁGICA!
Primeiro vamos precisar calcular a quantidade de elementos da P.A. usando a seguinte equação:
Para colocar isso no C++ vamos precisar usar uma expressão. Vamos colocar a subtração entre parêntesis para garantir que ela seja a primeira coisa a acontecer! Depois vamos efetuar a divisão e a soma:
Devido as regras de precedência, o parêntese será executado primeiro, seguido da divisão e por fim da soma. No código fica:
![]()
O próxima passo é calcular a soma da P.A usando a equação
Convertendo isso pra C++, fica assim:
Novamente usamos os parêntesis para garantir que a soma seja a primeira coisa a ocorrer. A multiplicação e a divisão têm a mesma precedência, mas pela regra de associatividade a multiplicação vai acontecer primeiro e por ultimo ocorre a divisão. No código fica:
![]()
Passo 5
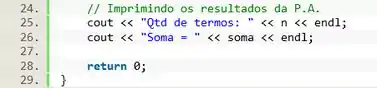
Prontinho. Com tudo calculado só falta a gente imprimir os resultados. A questão pede pra gente imprimir só a soma da P.A., mas é uma boa ideia imprimir também a quantidade de termos da P.A., pra ter certeza que tudo ocorreu certinho!
Usando o a gente primeiro imprime a quantidade de termos presentes na variável , e em seguida imprimimos o resultado da variável :
Passo 6
Por último, mas não menos importante, vamos testar o programa.
Vamos calcular a soma da P.A que começa em até com razão
Eu sei que essa P.A têm 100 termos e o resultado da soma é 10100. Se o programa estiver certinho vamos ter que ver esses dois resultados:
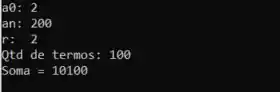
E aí está! A resposta do programa está correta, e o exercício está concluído!
Resposta
Exercício Resolvido #8
Adaptado de Lista de Exercícios UFRN – DCA800
O preço que um consumidor paga por um carro é composto pelo custo de fábrica, valor dos impostos e o valor do lucro do distribuidor. Faça um programa que gere o custo de fábrica de um carro e os valores pagos de imposto e pelo lucro do distribuidor, sabendo preço pago pelo consumidor. Dados: 45% de imposto sobre o custo de fábrica, e o lucro do distribuidor equivale a 12% sobre o custo de fábrica.
Passo 1
E aí, pessoal! Vamos pro exercício.
Antes de mais nada vamos escrever o cabeçalho do programa;
![]()
Essa questão fica mais fácil se a gente pensar em termos de entradas e saída do programa e vamos declarando as variáveis aos poucos.
Esse programa vai receber um único valor referente ao preço pago pelo consumidor. Este é um valor monetário, que sempre são valores reais com pelo menos duas casas decimais, então devem ser do tipo

E como saídas o programa vai imprimir o custo de fabricação do carro, o valor pago de impostos, e o valor do lucro do distribuidor.

Além disso temos alguns dados necessários para resolver a questão. o valor da taxa de imposto que é 45%, e a taxa de lucro do distribuidor que é de 12%. Esses valores devem ser constantes, pois não devem ser alterados ao longo do código

A parte mais chata foi essa em que a gente organizou o programa. Agora vamos juntos desenvolver o restante.
Passo 2
Agora a gente precisa receber o valor que o consumidor paga pelo carro, pois essa será a base dos cálculos da questão.
Usando o vamos solicitar o valor, e com o vamos armazenar o valor na variável adequada:

Passo 3
Beleza. Agora vamos desenvolver a contabilidade!

A questão afirma pra gente o preço do carro é a soma do custo de fabricação com o lucro e os impostos:
E também diz que os impostos e o lucro são calculados com base no custo de fábrica:
Porém, o programa recebe o valor do preço pago pelo consumidor. Então podemos rearranjar as equações para descobrir o valor do custo de fábrica:
Para escrever isso no C++ vamos precisar usar parêntesis para garantir que a soma no denominador ocorra antes da divisão:
No código teremos:
![]()
E com o custo de fabricação podemos calcular o valor do lucro e dos impostos:

Massa! Agora temos tudo calculado
Passo 4
Pra terminar o código só precisamos imprimir os resultados. Vamos utilizar o para imprimir o valor contido em cada variável, juntamente com uma frase que identifica o valor.
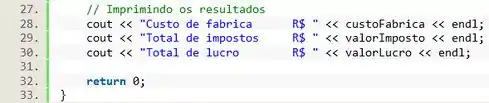
E prontinho, o código está finalizado
Passo 5
Pra finalizar, vamos testar o código. Vamos dizer que o consumidor paga um valor de em um carro. O resultado é:
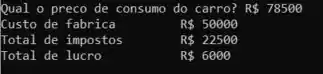
Se a saída do seu programa está igual a essa, então está tudo certinho! Questão concluída.
Resposta