cmath - Mais matemática com C++
Produzido por Gustavo BarbosaTeoria
E aí pessoal, aqui é o Juan do Responde Aí, e hoje vamos falar sobre a biblioteca cmath.
Matemática++
Até agora a gente viu as operações aritméticas básicas. Mas e onde estão as potências? Cadê as raízes, trigonometrias e logaritmos?
Não se preocupe, a Biblioteca Padrão do C++ fornece tudo isso dentro do header .
A cmath é uma biblioteca herdada da Linguagem C, e que fornece pra gente funções trigonométricas, hiperbólicas, exponenciais, potenciação, e muito mais.
Pra usar a biblioteca cmath a gente utiliza no começo do nosso código. E da mesma forma que a biblioteca iostream a gente precisa incluir o namespace da biblioteca padrão usando

E pronto! Agora podemos usar várias funções matemáticas que o C++ fornece pra gente.
Agora vamos falar sobre algumas das principais funções presentes na cmath.

Potenciação
As duas principais funções de potenciação presentes na biblioteca cmath são a pow e a sqrt

Para usar essas funções basta escrever o nome da função e dentro dos parêntesis colocar os valores que você quer calcular.
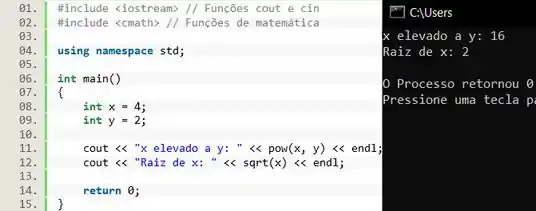
Na linha 11 a gente usou a função para calcular
E na linha 12 usamos a função para calcular
Trigonometria
As funções trigonométricas estão disponíveis também. Atenção, o C++ usa radianos.
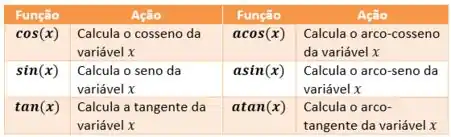
Usamos essas funções da mesma forma: basta escrever o nome da função e dentro dos parêntesis colocar os valores que você quer calcular.
Vamos ver alguns exemplos:

As funções trigonométricas trabalham em radianos, então é sempre bom definir uma variável contendo o valor de . E pra evitar que você altere o valor sem querer use o modificador const para criar uma constante inalterável, como fizemos na linha 08
Na linha 10 usamos a função para calcular o cosseno de . Na linha 11 calculamos o arco-seno de usando a função .
Já na linha 12 a gente usou uma expressão . Pela precedência, primeiro o C++ calcula as funções, nesse caso , e depois calcula a divisão . Dessa forma obtemos a cotangente.
Funções exponenciais e logarítmicas
As principais funções exponenciais e logarítmicas disponíveis são:

Vamos resolver alguns exemplos:

Na linha 8 vamos declarar uma constante com o valor de para facilitar.
Na linha 10 usamos a função para calcular o logaritmo natural de .
Na linha 11 usamos a função para calcular o logaritmo de na base .
Na linha 12 usamos a função para calcular o logaritmo de na base .
Outras funções comuns
Algumas outras funções da biblioteca cmath podem ser úteis.

Vamos ver um exemplo com as funções , e

Na linha 11 usamos a função para calcular valor absoluto da variável .
Na linha 12 usamos a função para calcular o maior valor entre as variáveis e . Com a função podemos calcular o menor entre as variáveis, como feito na linha 13
A diferença entre as funções , , e pode não ficar clara de primeira. Então vamos fazer o seguinte exemplo pra esclarecer:

O código pode ter ficado um pouco feio. Mas calma, que ele não assusta. São apenas muitos valores sendo impressas em uma mesma linha pra gerar essa tabela.
Saca só: O round efetua os arredondamentos de acordo com as regras matemáticas. O trunc simplesmente ignora os valores após o ponto decimal. O floor sempre busca diminuir o valor, mesmo quando esse valor já é negativo. E o ceil sempre aumenta o valor.
E por hoje é isso galera. Pra entender melhor, vamos fazer uns exercícios de fixação.