Funções que recebem arrays
Produzido por Gustavo BarbosaTeoria
Introdução
Fala aí, tudo tranquilo?
Você já deve ter se perguntado porque nos exercícios e exemplos que fizemos até esse momento nós não usamos arrays juntamente com funções. Isso acontece porque os vetores e as matrizes conversam de uma forma um pouquinho diferente com as funções do que uma variável comum.

Ficou curioso sobre isso? Então vem comigo que a gente vai destrinchar isso juntos!
Enviando um vetor para uma função
Vamos supor que você está trabalhando num projeto e precisa constantemente verificar os valores armazenados num determinado vetor que você utiliza no seu código. Para otimizar esse processo, você resolve fazer uma função que tem como objetivo imprimir os valores armazenados nesse vetor sempre que você usa essa função. Para que isso funcione, essa função precisa receber esse vetor como parâmetro.
É possível declarar essa função usando a seguinte sintaxe:
A função que descrevemos seria declarada da seguinte forma:
![]()
Perceba que a diferença de sintaxe entre passar um vetor e uma variável simples consiste apenas no uso de colchetes após o nome do vetor. Existem algumas regras para o uso desses colchetes:
- No caso de um vetor, o tamanho do vetor ser indicado dentro do colchete é algo opcional;
- Para um array multidimensional, como uma matriz, é necessário indicar o tamanho das dimensões, exceto a primeira.
Bom, de qualquer forma, isso não é uma diferença muito grande, então o que tem de tão diferente no uso de arrays em funções?
Calma que a gente vai chegar lá!
Antes disso, vamos ver o seguinte exemplo:
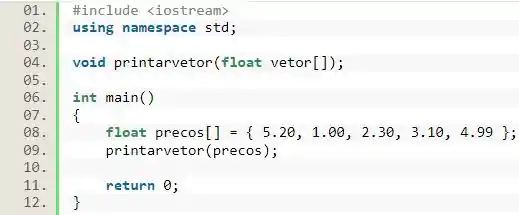
Nesse código, nós passamos o vetor como um parâmetro para a função . Perceba que, ao fazermos isso, nós colocamos apenas o nome do vetor como o parâmetro da função.
Mas o que exatamente nós estamos passando para essa função? Se colocarmos para imprimir na tela o array utilizando unicamente o seu nome como referência (ou seja, sem o índice de qualquer elemento armazenado nesse vetor) nós podemos entender isso melhor!
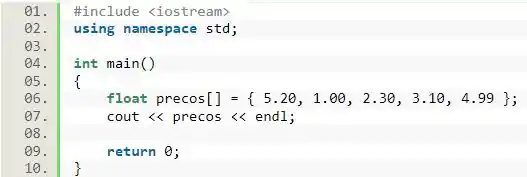
Ao colocarmos esse código para rodar, nós temos algo nesse formato:
![]()
Um endereço de memória! O que nós estamos enviando é um endereço de memória!
Para ser mais específico, esse é o endereço de memória do primeiro elemento do vetor. mas pera aí, como estamos enviando um endereço de memória, se modificarmos o que está armazenado nesse endereço, podemos modificar o valor do vetor?
Exatamente! Vetores, diferente de variáveis comuns, possuem os seus valores modificados quando os enviamos para as funções, pois, dentro das funções, temos acesso direto ao endereço de memória onde os elementos do vetor estão armazenados.

Nós já sabemos que um array é uma maneira de armazenarmos informação de forma indexada, ou seja, essa informação está armazenada numa estrutura específica na memória do nosso computador. Por causa disso, se o computador sabe a posição do primeiro elemento de um vetor, ele sabe a posição de todos, e com isso nós podemos trabalhar com todos os elementos desse vetor!
Agora vem a melhor parte disso tudo: para acessarmos a informação armazenada no vetor usando esse endereço de memória que foi enviado, basta fazermos o que fazemos desde o início, usar os colchetes! Ou seja, o nosso trabalho com o vetor se mantém o mesmo.
Sabendo disso, nós podemos concluir a função naquele código:
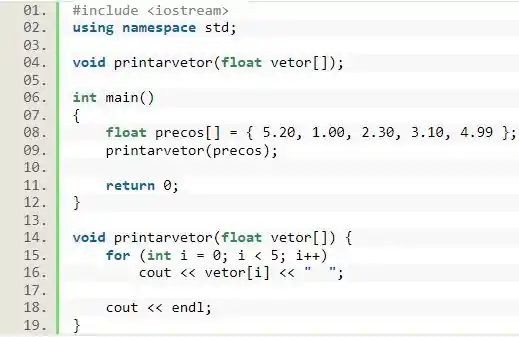
Vimos o caso de um vetor, mas e uma matriz? A situação será a mesma! A única diferença consiste no uso da regra para o colchete no momento de declarar a função.
Ou seja, se fôssemos utilizar uma função que recebe uma matriz, podemos declará-la da seguinte forma:

Agora que já entendemos como passamos um vetor ou uma matriz para uma função, vamos partir para as questões de fixação! Corre lá que eu te garanto que vai ter muita coisa boa!