Manipulando Matrizes
Produzido por Gustavo BarbosaTeoria
Introdução
Fala aí, tudo tranquilo?
Nesse tópico, vamos nos aprofundar mais no assunto de matrizes. Aprendendo a como preencher uma e a como manipular os seus elementos.
Tudo pronto pra começar? Então bora lá!

Preenchendo uma Matriz
Existem algumas maneiras de preenchermos uma matriz. É possível preenchê-la completamente com um comando apenas ou preenchê-la elemento por elemento.
Vamos começar explicando como preencheríamos uma matriz completamente. Para isso, vamos tomar como exemplo a seguinte matriz:
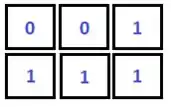
Nós podemos preencher essa matriz da seguinte forma:

Ou, para melhorar a nossa visualização:
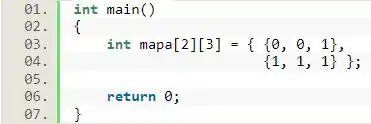
Perceba que é bem parecido com a maneira que usamos para preencher um vetor, no entanto, no lugar de cada elemento há um conjunto de dados formando uma linha, e não um dado isolado. Ou seja, nós agrupamos os elementos que compõem uma linha, usando uma notação semelhante àquela usada para vetores, com o início e o final de cada linha sendo marcada pelas chaves. As linhas são divididas por vírgula e todo o conteúdo da matriz fica dentro de uma chave externa àquelas usadas para as linhas, indicando a abertura e o fechamento da inclusão de dados.

Mas se estamos trabalhando com uma matriz grande não é muito usual que a preenchamos dessa forma, pois teríamos um comando muito grande. Há também a situação de querermos acrescentar os valores ao longo do código, e não no momento em que declaramos a matriz. Nesse tipo de situação, é melhor preencher os valores da matriz item por item.
Já deu pra perceber que há uma grande semelhança entre preenchermos os valores de um vetor e de uma matriz. Quando preenchemos cada dado individualmente, a única diferença está na quantidade de índices que usamos para localizar a posição do elemento que será acrescentado.
Para a matriz anterior, poderíamos preencher da seguinte forma:
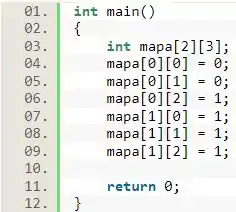
Eae, olhando para os índices usados, você conseguiu pegar a referência?

Isso mesmo! Do mesmo jeito de vetores, eles iniciam com e vão até o tamanho que foi definido menos ! Dessa forma, como declaramos a matriz com linhas, o índice das linhas (o primeiro) varia de até , e o mesmo princípio vale para o índice das colunas.
Operações
Para acessarmos qualquer valor de uma matriz, basta usarmos o nome da matriz e os índices referentes a sua posição. Vamos ver que usando isso, podemos manipular cada elemento de uma matriz.
Caso quiséssemos imprimir na tela o termo da primeira linha e da segunda coluna, bastaria o seguinte código:
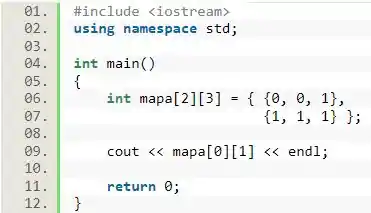
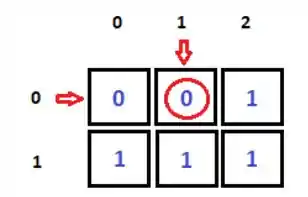
Nesse caso, o termo printado seria o , pois é aquele que está armazenado na posição :
Para realizarmos qualquer operação, basta usar a mesma maneira de referência, usando o nome da matriz e os índices da posição em que esse dado está localizado.
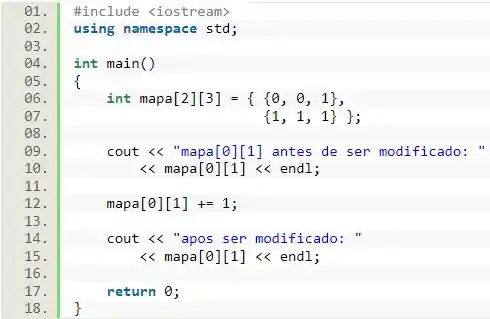
Nesse código, nas linhas 9 e 10 nós printamos o valor do que está localizado em , assim como feito anteriormente, mas dessa vez, vamos dar um passo extra logo em seguida. Na linha 12, nós modificamos o valor que foi impresso anteriormente na tela, somando 1. Perceba que ele foi tratado como uma variável normal, referenciada por . Após isso, nas linhas 14 e 15, nós imprimimos esse valor e constatamos que ele mudou. O resultado é esse:
![]()
Pra finalizar nosso papo, em C++ podemos trabalhar com array’s que possuem quantas dimensões quisermos. Mas na prática, nos limitamos a utilizar array’s com no máximo duas dimensões, por uma questão de simplificação. Por isso vimos só exemplos bidimensionais por aqui, mas se você precisar usar uma matriz com mais dimensões, fica tranquilo que as operações funcionam do mesmo jeito!
Agora que já sabemos como preencher uma matriz e como manipulamos os valores armazenados nela, podemos partir pros exercícios! Então me acompanha nessa!
Preenchendo uma Matriz
Operações
Exercícios Resolvidos
Exercício Resolvido #1
UFU – Facom - Programação 1 – Lista de Exercícios: Vetores e Matrizes
Declare uma matriz 5 x 5. Preencha com 1 a diagonal principal e com 0 os demais elementos. Escreva ao final a matriz obtida.
Passo 1
Fala aí, tudo tranquilo?
Para essa questão, nós vamos iniciar declarando a matriz. Como ela recebe somente valores inteiros, podemos declará-la como . Dessa forma, temos:
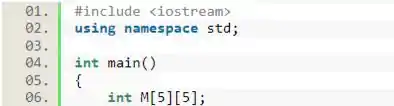
Além disso, como vamos ter que imprimir os valores da matriz, perceba que já fizemos a inclusão da biblioteca .
Passo 2
A seguir, nós temos que acrescentar os valores a essa matriz. Como esses valores possuem um padrão bem definido, é interessante fazermos um laço de for para ir acrescentando cada valor de acordo com a condição de se o valor está na diagonal principal (os índices das posições forem iguais) ele será 1, caso contrário, ele será 0.
Para passarmos por todos os valores dessa matriz, é importante que façamos dois laços de . O primeiro para variar o índice das linhas e o segundo, interno ao primeiro, para variar o índice das colunas. Dessa forma, podemos ir preenchendo todos valores indo de linha por linha.
![]()
Agora, basta usarmos e para as condições que colocamos que definimos.
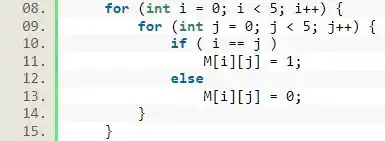
Passo 3
Para finalizar, basta printarmos todos os termos dessa matriz. Para fazer isso, temos que usar do mesmo esquema de laços de , passando por todos os termos da matriz e usando a função . Isso é algo muito bom, pois podemos aproveitar o laço de for que já fizemos e apenas acrescentar o comando para imprimir o valor após ele ser passado para a matriz:
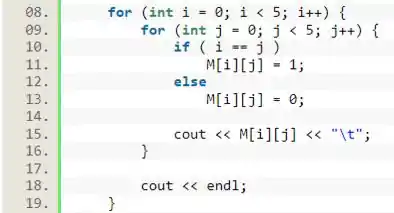
Perceba que usamos o comando de imprimir duas vezes. Uma dentro do que varia a coluna, na linha 15, e outro dentro apenas do que varia a linha, na linha 18 do código. O primeiro serve para imprimirmos o valor e dar uma distância entre valores da mesma coluna, usando o . O segundo serve para fazermos uma quebra de linha no momento em que mudamos para a próxima linha da matriz, melhorando a nossa organização no momento de imprimir a matriz.
Resposta
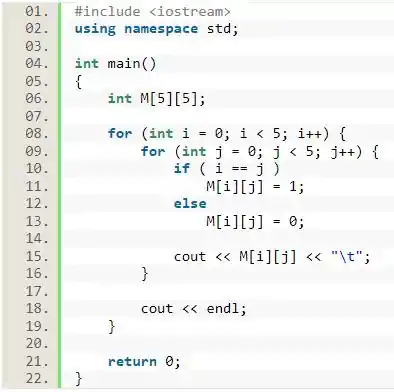
Exercício Resolvido #2
UFC – SMD - Programação 1 – Lista de Exercícios Sobre Matrizes
Crie uma matriz M1 de dimensão 4 x 4. Seus valores são exatamente a soma dos índices da linha com a coluna. Mostre na tela cada elemento de M1.
Passo 1
Fala aí, tudo beleza?
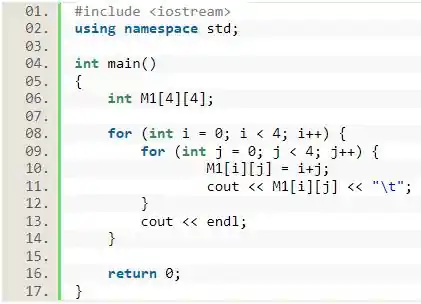
Como o enunciado falou que devemos mostrar os valores de M1, vamos começar o nosso código incluindo a biblioteca , que nos permite usar a função para imprimir valores na tela.
![]()
Após isso, vamos declarar a matriz. Como ela só recebe valores inteiros, podemos declará-la como . Além disso, o enunciado já nos deu os valores de suas dimensões quando nos disse que ela é 4 por 4.
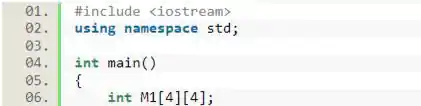
Passo 2
A seguir, nós temos que acrescentar os valores a essa matriz. Como esses valores possuem um padrão bem definido, é interessante fazermos um laço de for para ir acrescentando cada valor de acordo com a condição dos valores serem iguais a soma do índice da linha com o índice da coluna, ou seja, .
Para passarmos por todos os valores dessa matriz, é importante que façamos dois laços de . O primeiro para variar o índice das linhas e o segundo, interno ao primeiro, para variar o índice das colunas. Dessa forma, podemos ir preenchendo todos valores indo de linha por linha.

Passo 3
Para finalizarmos, vamos usar os laços de que já fizemos para printarmos os valores da matriz.
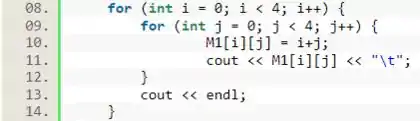
Perceba que usamos o “/t” para indicar uma distância entre 2 termos da matriz e o para indicar o término de uma linha.
Resposta
Exercício Resolvido #3
UFU – Facom - Programação 1 – Lista de Exercícios: Vetores e Matrizes
Faça um programa que permita ao usuário entrar com uma matriz de 3 x 3 números inteiros. Em seguida, gere um array unidimensional pela soma dos números de cada coluna da matriz e mostrar na tela esse array. Por exemplo, a matriz:

Vai gerar um vetor, onde cada posição e a soma das colunas da matriz. A primeira posição será 5 + 1 + 25, e assim por diante:
![]()
Passo 1
Fala aí, tudo tranquilo? Então bora lá!
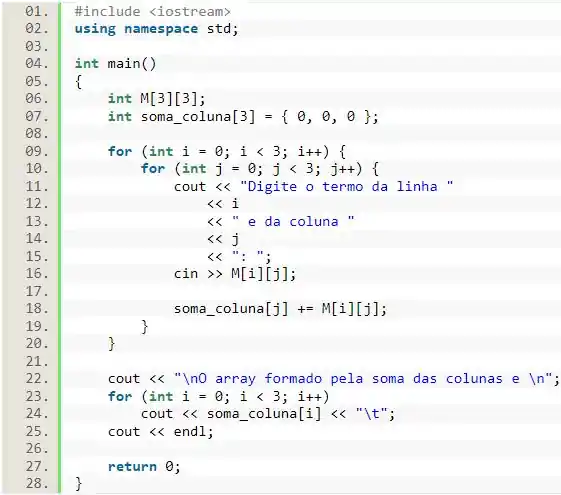
Nessa questão, vamos iniciar incluindo a biblioteca , pois vamos ter que receber valores do usuário e imprimir valores na tela. Além disso, já dentro da função vamos declarar a matriz que o usuário vai passar os valores e o vetor que vai receber a soma dos valores da coluna.
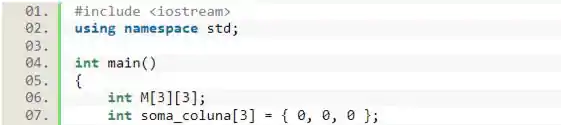
Para o caso do vetor, perceba que iniciamos ele com os 3 valores sendo 0. Isso ocorre porque vamos usá-lo como um acumulador e, para isso, é interessante que ele possua um valor inicial neutro.
Passo 2
A seguir, vamos fazer aquele laço de duplo para passarmos os valores para a matriz. Dessa vez, vamos printar uma mensagem para indicar que o usuário deve digitar o número (usando ) e depois vamos passar o valor digitado pelo usuário para a matriz (usando ).
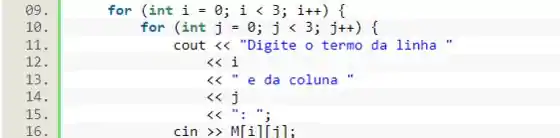
Passo 3
Agora, precisamos passar o valor da soma dos elementos das colunas para o vetor. Nesse caso, para não precisarmos passar valor por valor em um código maior, podemos aproveitar o laço de e fazer o vetor já ir acumulando os valores recebidos pela matriz.
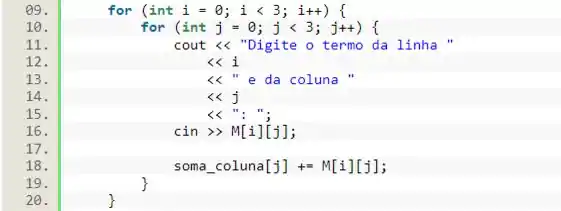
Perceba que usamos o índice para a posição dentro do vetor, pois ele é o índice das colunas.
Passo 4
Por fim, vamos printar os valores do vetor. Para isso, vamos printar uma mensagem inicial e depois, dentro de um laço de simples, vamos printar valor por valor, dando uma distância entre cada um deles.
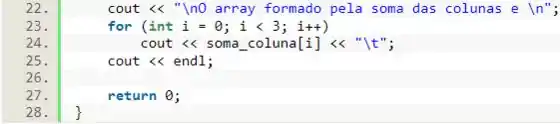
Resposta
Exercício Resolvido #4
UFU – Facom - Programação 1 – Lista de Exercícios: Vetores e Matrizes
Gerar e imprimir uma matriz de tamanho 10 x 10, onde seus elementos são da forma:
Passo 1
Eae, tudo tranquilo?
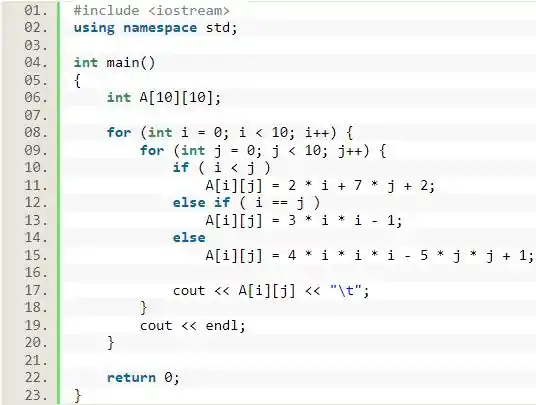
Nessa questão, vamos iniciar declarando a matriz com as suas dimensões . Além disso, vamos declará-la como , pois, como é mostrado no enunciado, os seus elementos são inteiros que vem de operações com números dos índices de suas posições.

Passo 2
A seguir, vamos passar os valores para essa matriz. Usando o laço de duplo, com representando o índice das linhas e sendo o índice das colunas, vamos usar e para passar os valores de acordo com cada condição do enunciado.
Nesse caso, vamos seguir a ordem do enunciado, começando por , depois e, por fim, , que é a única condição que falta, por isso usando apenas o

Passo 3
Agora, basta printarmos a matriz, para isso, vamos aproveitar os laços de já feitos. Dentro do laço de do , índice das colunas, nós imprimimos cada termo dado uma distância /t entre cada termo. Dentro somente do laço de do , índice das linhas, nós fazemos uma quebra de linha. Dessa forma, a impressão da matriz está finalizada.
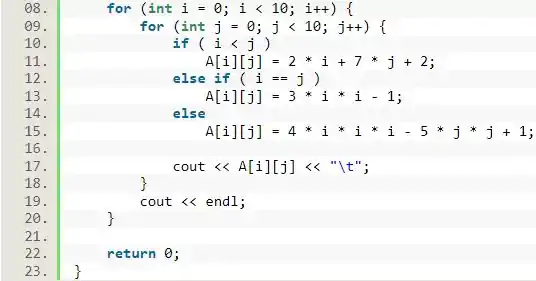
Resposta
Exercício Resolvido #5
UFC – SMD - Programação 1 – Lista de Exercícios Sobre Matrizes - Adaptada
Crie um programa que receba um valor inteiro, que seja no máximo 20, como input do usuário. O programa deverá realizar as seguintes tarefas:
- Preencher uma matriz de inteiros quadrada de ordem igual ao valor passado para o procedimento, com elementos aleatórios.
- Exibir o conteúdo da matriz.
- Identificar qual é o maior elemento da matriz.
Passo 1
Eai, tudo beleza?
Nessa questão, vamos resolvendo letra por letra.
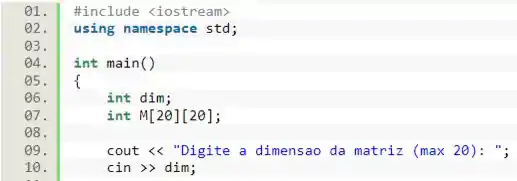
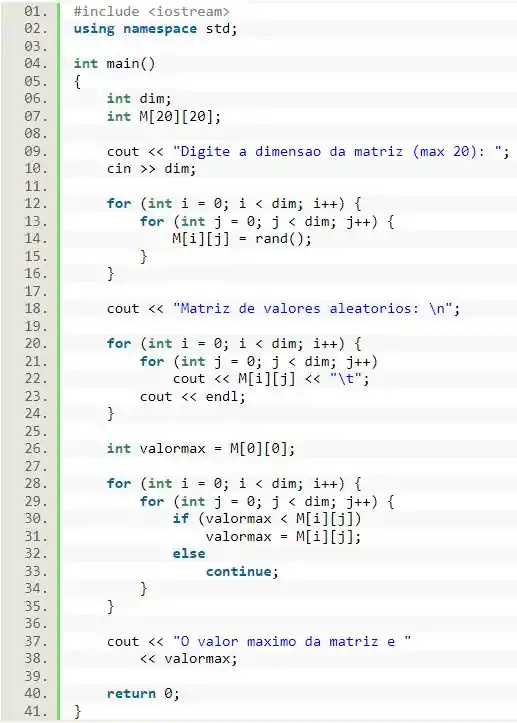
Vamos iniciar o nosso código declarando uma variável que vai receber a dimensão da matriz e a própria matriz, que possui dimensões máximas . Em seguida, vamos passar um valor passado pelo usuário para a variável .
Agora, basta passarmos os valores aleatórios para a matriz. Para isso, usamos um laço duplo de , que onde cada vai variar de 0 até o valor de . Dentro desses laços vamos passar os valores para a matriz, usando a função , que nos retorna um número aleatório.

Passo 2
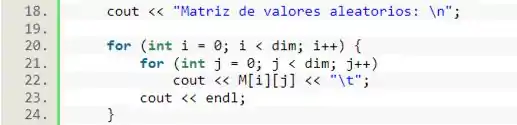
No item b), precisamos imprimir essa matriz na tela. Para isso, usaremos o mesmo esquema de laços de do item anterior, mas dessa vez, colocaremos o comando para imprimir o valor de cada termo e o comando para distanciá-los. Além disso, dentro apenas do laço que varia as linhas , vamos fazer uma quebra de linha.
Passo 3
No item c), precisamos achar o valor máximo da matriz. Para isso, vamos declarar uma variável , que vai receber um valor qualquer da matriz (nesse caso, escolhemos o primeiro valor).
A lógica para acharmos o valor máximo, é pegar um valor da matriz e compararmos com todos os outros e, sempre que achamos um valor maior do que aquele que estamos usando, fazemos a nossa variável receber esse valor. Dessa forma, ao final da comparação, o maior valor da matriz estará armazenado em .
Dessa forma, vamos utilizar aquele mesmo laço duplo de para passarmos por todos os valores da matriz. Dentro do laço, vamos utilizar o e o para fazermos a comparação de valor. Se for menor de o valor armazenado na matriz, recebe esse elemento da matriz. Caso contrário, nada acontece.
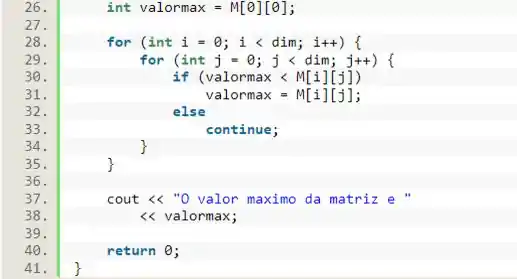
Ao término do , basta imprimirmos esse valor na tela.
Resposta
Exercício Resolvido #6
UFU – Facom - Programação 1 – Lista de Exercícios: Vetores e Matrizes
Leia uma matriz de 3 x 3 elementos inteiros. Calcule a soma dos elementos que estão acima da diagonal principal.
Passo 1
Eai, tudo beleza?
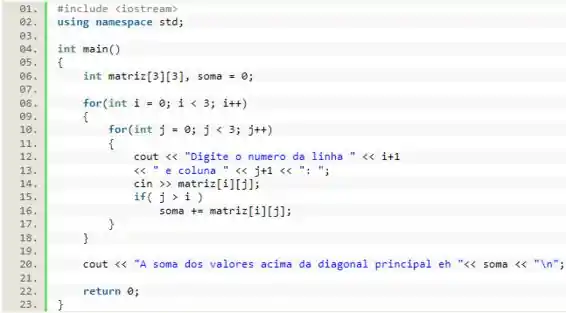
Nessa questão, nós devemos pedir ao usuário os termos de uma matriz e calcular a somar de determinados elementos. Para isso, vamos iniciar o nosso programa incluindo a biblioteca e declarando a matriz e a variável que vai guardar a soma.

Perceba que, como vamos utilizar e variável como uma acumuladora, devemos iniciá-la com o valor .
Passo 2
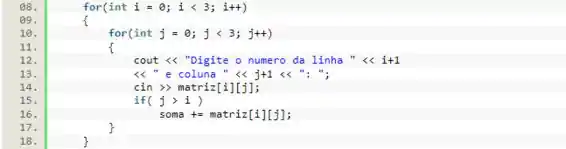
Em seguida, vamos dois laços de , de forma a passarmos por todos os elementos dessa matriz. Dentro do laço de mais interno, vamos pedir para que o usuário digite o número para colocar na matriz e vamos passar esse valor ao elemento dessa matriz.

Ainda dentro desse laço de vamos calcular a soma pedida. Numa matriz, os elementos que estão acima da diagonal principal, possuem o índice da coluna maior que o da linha. Sabendo disso, vamos utilizar um condicional para checar se esse elemento está acima da diagonal principal e, em caso positivo, vamos somar o seu valor à variável .
Passo 3
Por fim, basta imprimirmos esse valor na tela e encerrarmos a nossa função :

Resposta
Exercício Resolvido #7
UFU – Facom - Lista de Exercícios: Vetores e Matrizes - adaptada
Faça um programa que leia uma matriz 3 x 6 com valores reais.
- Imprima a soma de todos os elementos das colunas ímpares.
- Imprima a média aritmética dos elementos da matriz com exceção da segunda coluna.
Passo 1
Eai, tudo tranquilo?
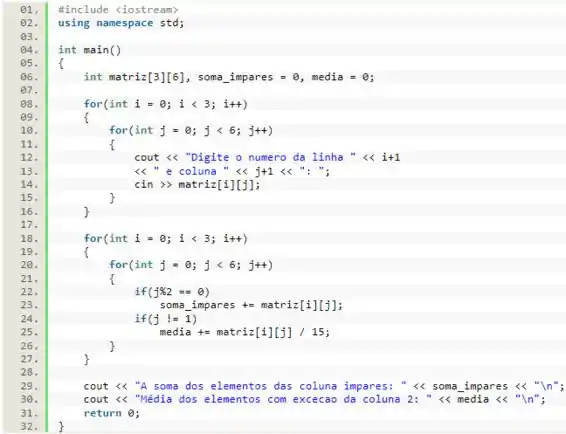
Nessa questão, devemos pedir ao usuário uma matriz e, após isso, vamos calcular a soma e a média de determinados elementos. Vamos iniciar o nosso código incluindo a biblioteca para recebermos os valores e imprimirmos mensagens na tela e, já dentro da função , vamos declarar a nossa matriz, uma variável para acumular a soma e uma variável para acumular a média.

Passo 2
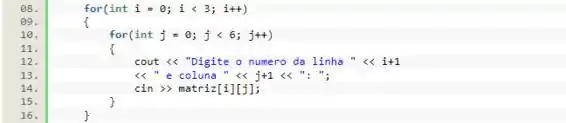
Agora, vamos fazer uma dois laços de , um dentro do outro, para passarmos por todos os termos da matriz. Dentro desses laços, vamos imprimir uma mensagem indicando ao usuário que ele deve passar os valores para a matriz.
Passo 3
Em seguida, vamos iniciar outros 2 laços de , no mesmo formato que os anteriores para calcularmos o que nos foi pedido. Como precisamos da soma dos valores das colunas ímpares, vamos fazer um condicional para checa isso. Perceba que, ao invés dos termos com índices ímpares, vamos checar se esses termos possuem índices pares, pois os índices na matriz iniciam no e não no .

Ainda dentro do mesmo laço, vamos fazer um condicional para checar se o termo não pertence à coluna , ou seja, a coluna de incide na matriz. Em caso positivo, vamos somar o valor do elemento dividido por (total de elementos da matriz menos uma coluna) ao valor da variável média.
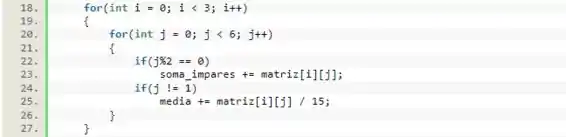
Por fim, basta imprimirmos esses valores.

Resposta
Exercício Resolvido #8
UFU – Facom - Programação 1 – Lista de Exercícios: Vetores e Matrizes - adaptada
Faça um programa que leia uma matriz de linhas e colunas contendo as seguintes informações sobre alunos de uma disciplina, sendo todas as informações do tipo inteiro:
- Primeira coluna: número de matrícula.
- Segunda coluna: média das provas.
- Terceira coluna: média dos trabalhos.
- Quarta coluna: nota final.
Ao final do programa, imprima essa matriz.
Passo 1
Eai, tudo beleza?
Vamos iniciar a nossa questão incluindo a biblioteca e, na função , vamos declarar a nossa matriz.

Após isso, vamos iniciar laços de , um interno ao outro, para passarmos por todos elementos da matriz.
![]()
Passo 2
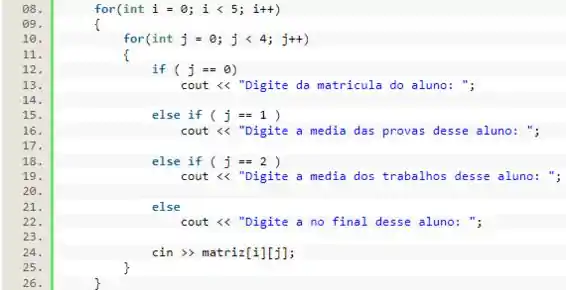
Nos laços de , vamos checar o índice da coluna para imprimirmos uma mensagem personalizada para o usuário. No caso de termos o usuário deve passar uma matrícula, nesse caso, nós imprimimos a seguinte mensagem.

Vamos fazer o mesmo para o restante dos índices e após todos os condicionais, vamos passar o valor informado para o elemento da matriz:
Passo 3
Por fim, vamos fazer outra estrutura composta por 2 laços de para imprimirmos os valores dessa matriz:
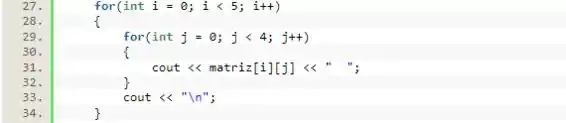
Resposta