Introdução às Funções
Teoria
Introdução
Fala ae, tudo beleza? Nessa aula nós vamos aprender sobre uma estrutura de código muito importante para todo programador, as funções. Então bora entender o que são as funções e como declará-las no nosso código.
O que é uma função?
Suponha que você está programando e, durante o processo, aparece uma parte do código que fica se repetindo e você tem que ficar reescrevendo ela o tempo todo, algo como receber dois números e calcular a soma entre eles. Ficar repetindo códigos parecidos é considerado uma má prática de programação, pois torna o seu código mais extenso e difícil de ser compreendido.
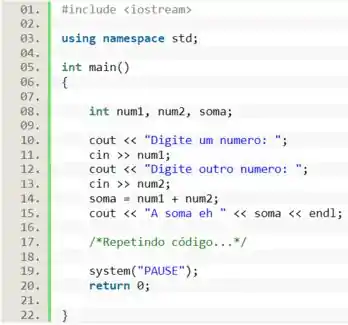
Uma alternativa para isso, é estruturar o seu código em funções, o que irá permitir criarmos uma estrutura de código que queremos usar várias vezes e, sempre que precisarmos, podemos apenas chamá-la. Dessa forma, teríamos algo assim:
Nesse segundo caso, nós escrevemos uma função para fazer o que queríamos no código anterior e, dessa forma, apenas chamamos ela dentro da função para executar o código definido anteriormente.
Com isso, podemos entender as funções como uma sub rotina de um programa, onde você escreve um código que poderá ser reutilizado ao longo do programa (sem precisar ser repetido!), de forma a melhorar a estruturação do seu código.
Estrutura de uma função
Para se declarar uma função, inicialmente precisamos de 2 coisas:
- O tipo de dado que será retornado:
Ele é indicado no momento em que definimos a função. Se declaramos função como
Significa que essa função, ao fim de sua execução, irá retornar para o sistema um dado do tipo .
O dado de retorno da função é o que queremos obter quando usamos aquela função. Por exemplo, se precisarmos de uma função para calcular um determinado somatório, o resultado desse somatório será o valor que deverá ser retornado pela função.
A própria função , que define o código a ser executado, segue esse padrão.
Ela é declarada com um antecedendo, o que indica que ela retornará um valor inteiro ao final da sua execução. Por padrão, colocamos para ela retornar ao final de sua execução. O retorno do valor , indica que a função foi executada com sucesso e que ela será encerrada.
Se tiver algum código dentro de uma função após um ser lido, esse código não será executado, pois o indica o fim da função.
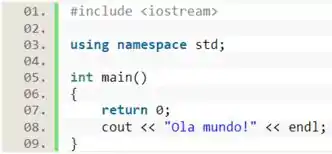
Nesse caso, a linha 8 não será executada e o programa não irá imprimir “Olá mundo”.
Existe ainda, funções que não retornam nenhum valor, essas funções são declaradas como .
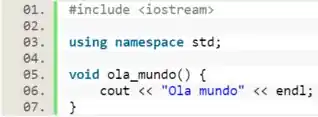
Perceba que a função é um função que, ao ser chamada, imprime na tela. Nesse caso, ela cumpre o seu objetivo sem precisar retornar nenhum valor ao sistema.
- Os parâmetros:
Os parâmetros de uma função são dados externos a ela que enviamos sempre que a chamamos. Esses parâmetros são indicados no momento em que vamos criar essa função. Vamos analisar como exemplo uma função que recebe dois números como parâmetros e calcula a divisão entre eles.
Para criarmos essa função, teríamos que declará-la da seguinte forma:
Para usá-la no nosso código, temos que chamá-la dentro da função . Para isso, precisamos passar os dois parâmetros definidos.
Perceba que os nomes que utilizamos para os parâmetros quando definimos a função não precisam ser os mesmos nomes utilizados quando passamos os valores dos parâmetros dentro da função .
Agora que já temos alguns conhecimentos sobre funções e como elas são declaradas, que tal irmos para os exercícios de fixação?
Estrutura de uma função
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Em diversas linguagens de programação, como C, C++, Python e Java, são utilizadas funções para melhorar a estrutura do código. Nesse contexto, explique como é estruturada uma função em C++.
Passo 1
Eai, tudo beleza?
Nessa questão, precisamos descrever a estrutura de uma função.
Para declararmos uma função, inicialmente precisamos definir o tipo de variável que ela irá retornar e a o que essa função receberá como parâmetro.
Após isso, teremos o código interno à função que será finalizado com o comando de retorno e, com isso, encerramos a função.
Resposta
Exercício Resolvido #2
UFF – Telecomunicações - Explorando o uso de funções – Questão 1
Fazer uma função que calcula a enésima potência de uma variável real x:
Passo 1
Eai, tudo beleza?
Nessa questão, vamos, inicialmente, definir o que a função vai receber como entradas, para fazer o que se pede. Para que a função calcule o valor de , precisamos quem ela tenha como entrada o e o . Vamos definir o como , pois ele pode assumir qualquer valor, e o como , pois ele é um número inteiro.
Como queremos que a função retorne , e é um , podemos definir o retorno da função como um . Com isso, temos:
Passo 2
Agora, vamos implementar o algoritmo de potenciação. Como a potenciação é a multiplicação de um número por ele mesmo vezes, vamos usar um loop. E para armazenar o produto dessas multiplicações, vamos definir uma variável , de valor inicial , que vai receber o resultado da função.
Com isso, vamos implementar o laço de para calcularmos a potenciação e armazená-la na variável . A cada iteração (volta no loop) vamos multiplicar esse produto por mais uma vez, e faremos isso vezes. Por isso, ali na linha 5, definimos que a variável de comando vai variar entre e .
Daí, dentro do , em vez de escrevermos , vamos usar o operador de atribuição por multiplicação e escrever . É um jeito mais compacto de escrever a mesma coisa.
Resposta
Exercício Resolvido #3
IFC - Curso de Graduação em Ciência da Computação - Algoritmos - Marcelo Cendron – Questão 7
Faça uma função que recebe um valor inteiro e verifica se o valor é par. A função deve retornar se o número for par e se for ímpar.
Passo 1
Eai, tudo beleza?
Vamos primeiro declarar a função, indicando o tipo do seu retorno e o que ela recebe. Como é dito pelo enunciado, os possíveis retornos são e , com isso, sabemos que vamos declarar a função como . Além disso, a entrada da função é um valor inteiro. Dessa forma temos:
Passo 2
Agora, precisamos acrescentar os condicionais para verificar se é par ou ímpar, retornando 1 para par e 0 para ímpar.
Resposta
Exercício Resolvido #4
IFC - Curso de Graduação em Ciência da Computação - Algoritmos - Marcelo Cendron – Questão 8
Faça uma função que recebe um valor inteiro e verifica se o valor é positivo, negativo ou zero. A função deve retornar 1 para valores positivos, -1 para negativos e 0 para o valor 0.
Passo 1
Eai, ta tudo beleza?
Para começarmos a fazer essa função, vamos primeiro definir como vamos declará-la. Pelo enunciado, temos 3 possíveis valores de retorno: , e . Com isso, podemos declarar essa função como e, como ela recebe um valor inteiro como entrada, temos um como parâmetro. Declaramos a função e, dentro dos parênteses, o seu parâmetro. É um pouco parecido com a nomenclatura na matemática ne?
Passo 2
Agora, temos que acrescentar os condicionais, ou seja, os nossos . Fazemos com que a função retorne para , para e para .
Como só existem 3 possibilidades para um número inteiro (positivo, negativo ou 0), não precisamos especificar a última condição, pois ela é a restante, por isso utilizamos apenas o .
Resposta
Exercício Resolvido #5
Elaboração Própria
Na eletrostática, há o estudo do campo elétrico gerado por cargas. Sabendo que a intensidade do campo elétrico num ponto (x, y, z) proveniente de uma carga puntiforme localizada na origem do sistema de coordenadas é é dado por:
onde e , desenvolva uma função em C++ que calcule a intensidade desse campo e a retorne. A função deve receber como parâmetros o valor da carga (em ) e as 3 coordenadas, todos como valores reais.
Passo 1
Eai, tudo tranquilo? Então vamos lá!
O primeiro passo é analisarmos como vamos declarar essa função. Por meio do enunciado, sabemos que os 4 parâmetros que serão recebidos pela função são do tipo ou , já que eles são números reais. Além disso, como essa função irá retornar o valor do campo elétrico, ela deverá ser declarada como ou .
Vamos escolher o para uma melhor precisão, mas poderia ser qualquer um dos dois, pois o enunciado, ao não especificar, nos deu essa liberdade.
Dessa forma, temos o seguinte:
Passo 2
Para nos auxiliar, vamos criar duas variáveis: , para armazenar o valor da constante eletrostática, e , para armazenar o módulo do campo. Vamos incluir a biblioteca para facilitar as nossas contas.
Da biblioteca , vamos utilizar a função , que serve para utilizarmos a potenciação. De forma que: . Assim, temos:
Passo 3
Por fim, o que precisamos fazer é acrescentar a equação do campo elétrico e retornarmos o valor obtido.
Resposta
Exercício Resolvido #6
PUCRS – Exercício sobre Funções e Procedimentos
Faça uma função que recebe por parâmetro o raio de uma esfera e retorna o seu volume ( )
Passo 1
Eai, tudo beleza?
Nessa questão, vamos iniciar declarando a nossa função. Como vamos tratar de operações como divisão e potenciação, vamos tratar todos as variáveis como . Para isso, vamos declarar a nossa função de forma que ela retorne um e receba como parâmetro um de nome .
Passo 2
Agora, dentro da nossa função, vamos fazer com que ela retorne o valor do volume. Sabemos que o volume é igual a , logo, basta fazermos a função retornar esse valor. Para isso, vamos adotar pi como .
Resposta
Exercício Resolvido #7
PUCRS – Exercício sobre Funções e Procedimentos
Faça uma função que recebe a idade de uma pessoa em anos, meses e dias e retorna essa idade expressa em dias.
Passo 1
Eai, tudo beleza?
Basicamente, vamos fazer uma função que deve converter algumas unidades de tempo. Como a quantidade de dias, meses e anos podem ser mensuradas com valores inteiros, vamos definir o retorno e os parâmetros da função como do tipo inteiro.
Vamos fazer essa função receber 3 parâmetros: , e :
Passo 2
Agora, basta fazermos uma conversão de meses para dias e de anos para dias. Sabemos que um mês tem, em média, 30 dias, enquanto 1 ano tem, em média, 365 dias. Vamos multiplicar a quantidade de meses por 30 e a quantidade de anos por 365 e somar com a quantidade de dias. Essa conta deve resultar na quantidade de total de dias:
Por fim, basta retornarmos esse valor:
Resposta
Exercício Resolvido #8
PUCRS – Exercício sobre Funções e Procedimentos
Faça uma função que receba um valor inteiro e positivo e calcula o seu fatorial.
Passo 1
Eai, tá tudo tranquilo?
Para essa questão, vamos elaborar uma função para calcular o fatorial de um número. Inicialmente, vamos declarar a nossa função. Como ambos os valores de parâmetro e de retorno da função são do tipo inteiro, podemos declará-la da seguinte forma:
Passo 2
Vamos calcular o fatorial. Para isso, vamos declarar uma variável acumuladora. Como essa variável terá que acumular o valor de um produtório, vamos declará-la com valor inicial :
Passo 3
A seguir, vamos calcular o fatorial. Para isso, vamos fazer um laço de que faça o valor de uma variável ir de até o valor recebido como argumento. Dentro desse laço, nós fazemos o acumulador ir sendo multiplicado por cada novo valor de . Dessa forma, ao final do loop, a variável acumuladora terá o valor do fatorial que queríamos calcular.
Por fim, basta retornarmos o valor armazenado em .
Resposta
