Curvas Bidimensionais
Produzido por Gustavo BarbosaTeoria
Alguns aspectos introdutórios.
Iaê pessoal, tudo beleza?
Bem galerinha, hoje iremos conversar um pouco sobre as curvas bidimensionais.Todo programa é composto por três blocos de códigos: sempre começamos com a entrada de dados, em seguida escrevemos algum código de processamento e finalizamos com a saída de dados.
Por exemplo, se você for comprar um remédio em uma farmácia, a entrada de dados é você pedindo o remédio ao balconista, após isso, o balconista vai pegar o produto na dispensa se caracterizando como o processamento do pedido e por fim, o processo é finalizado quando ele entrega o produto na sua mão, que é a saída de dados.
Em programação, existem algumas formas de imprimir a saída de dados: como um texto ou apenas um único valor por exemplo, e hoje veremos um outro tipo de saída de dados que são os gráficos de curvas bidimensionais.
Por exemplo, imagine que você está fazendo uma análise de quanto você gastou por mês e monta uma tabela com os seguintes valores:
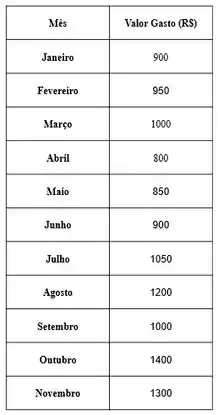
Apesar da tabela ser uma excelente forma de visualização, uma visualização gráfica ficaria melhor não acha? Se duvida ainda, observa só esse gráfico abaixo:
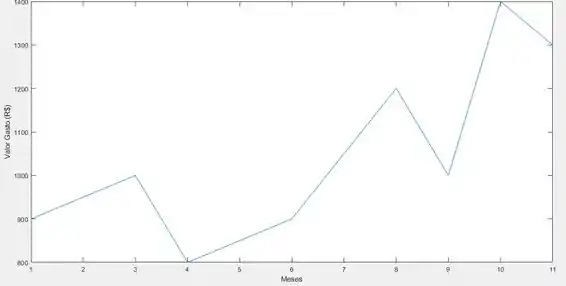
Uma simples representação gráfica nos permite observar diversas características do seu gasto com mais facilidade, por exemplo, nos meses iniciais do ano você gastou menos que nos meses finais, além disso abril foi o mês de menor gasto e outubro, o de maior.
Ou seja, uma saída de dados gráfica nos permite ter uma melhor compreensão das tendências e da natureza dos dados.
Você deve estar doidinho para saber como montar aquele gráfico, né? Calminha aí, segura um pouco o ânimo que vamos aprender agorinha mesmo.
Comando Plot
O primeiro código que iremos aprender é o comando , ele é a plotagem mais básica que temos dentro do Matlab e foi esse comando que utilizei para realizar a plotagem do exemplo passado.
Por exemplo, vamos plotar o exemplo mostrado!
Primeiramente, criaremos a entrada de dados, ou seja, vamos inserir os vetores que queremos plotar, um vetor que representa os meses e um vetor que contém os gastos:
Uma vez que criamos os vetores vamos chamar a função plot
Aqui o Matlab cria um gráfico, colocando a variável como o eixo , e a variável como o eixo .
A sintaxe é sempre essa, o primeiro conjunto de dados no é o eixo horizontal e o segundo, o vertical. Não esquece! 😉
Uma vez que criamos o gráfico, vamos inserir os nomes nos eixos pra que quem veja o gráfico consiga entender o que os dados representam. Fazemos isso no eixo da seguinte forma:
E aqui iremos nomear o eixo :
Com isso, chegamos no gráfico que vimos ali em cima! Dá uma conferida em como fica o código completinho:
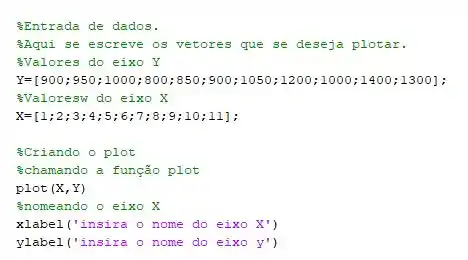
Mas e se quisermos inserir mais de uma curva dentro do gráfico?
É bem simples, como exemplo vamos criar um gráfico com as funções e :
Para isso, vamos começar criando o vetor de entrada de dados. Vamos pegar o intervalo de a , com um intervalo de pontos bem pequeninho pra curva parecer contínua:
Agora iremos criar os vetores seno e cosseno aplicando as funções pré-definidas do matlab no vetor que criamos:
Uma vez que já criamos os vetores seno e cosseno, vamos criar os gráficos. Usamos mais uma vez a função , mas agora colocamos um par de dados pra cada curva que queremos criar:
A primeira curva é do seno e tem o vetor como eixo horizontal e o vetor como eixo vertical. A segundo, do cosseno, tem os vetores e como horizontal e vertical, respectivamente.
Aqui fizemos duas curvas, mas não precisa parar por aí! Se tivermos inúmeros plots, apenas precisamos escrever os pares de pontos e dentro da função plot.
Agora iremos nomear os eixos:
Escrevendo o código no Matlab temos o gráfico:

As curvas tão aí como queríamos, porém ficou difícil dizer quem é quem né? Além disso, fica o questionamento: “O quê que esse gráfico está medindo mesmo?”
Então, para respondermos essas perguntas precisamos de dois comandos, o primeiro que vai colocar um título no nosso gráfico, e o segundo que vai criar uma legenda pras curvas:
Na função escrevemos a descrição das curvas na mesma ordem que usamos pra criar o plot. Implementando no Matlab e executando o código a curva se torna:
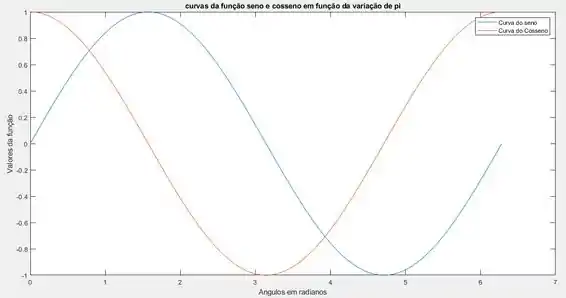
Agora sim, qualquer um que encontra esse gráfico consegue entender exatamente o que tá acontecendo!
Mas não para por aqui! Além do comando existem outros tipos de gráfico no matlab que você pode procurar e usar em casos específicos, mas como já vimos bastante coisa, por hoje encerramos por aqui.
Lembra que sempre é bom praticar pra tudo ficar mais claro na sua mente. Por isso, não esqueça de olhar os exercícios que preparamos especialmente para você, ok?
Até maaaaaaais!
Comando Plot
Exercícios Resolvidos
Exercício Resolvido #1
“Elaboração Própria”
Construa em Matlab o gráfico da seguinte função:
com a variável variando entre os valores
Passo 1
A questão está pedindo pra plotar o gráfico da função
entre o intervalo de:
Antes de começarmos a resolver a questão precisamos nos lembrar de um detalhe.
O sistema de plotagem de uma curva com o Matlab consiste em calcular o valor da função para vários valores de e imprimir esses valores em uma janela gráfica chamada de gráfico, ou seja, o Matlab não gera uma curva.
Então o que ele gera né?
Na real é um bocado de pontinhos bem próximos um do outro, que ao aparecer na nossa tela do computador sob o formato de um gráfico dá a impressão que é uma curva contínua. Mas se dermos um zoom gigantesco iremos ver que na verdade é um bocadinho de pontinhos juntos, belezinha?
Em outras palavras, não plotamos a função. Nós plotamos um vetor que contém os valores dessa função em vários pontos. Nós sempre plotamos um vetor!
Então antes de plotar qualquer função precisamos informar o quão perto esses pontinhos estão, e pra isso precisamos criar um vetor X e implementá-lo, pois é a ferramenta mais simples para se fazer isso.
E vamos utilizar o incremento da criação de vetores para informar o quão perto esses pontinhos devem estar, em geral, utiliza-se um incremento da ordem de 0.01, por isso é comum encontrar esses vetores na seguinte forma:
E esse vetor está nos informando que o X vai sair de -4 e vai somar 0.01 até chegar no 4, ou seja, a distância entre dois pontos é da ordem de 0.01.
Bem pertinho né?
Agora que sabemos disso vamos montar o nosso algoritmo.
Primeiramente para a criação do código precisamos criar o algoritmo para entender o que o código faz:
- Entrada de dados, aqui vamos implementar os valores de X.
- Cálculo da função de X
- Plotagem da função
- Nomeando os eixos e o título do gráfico.
Passo 2
Primeiro passo é a criação do vetor do vetor X para o cálculo da função e impressão do gráfico.
Uma vez que criamos o vetor X vamos calcular os valores da função, e lembrando de um detalhezinho. Aqui temos uma operação vetorial, ou seja, queremos que essa função se calcule em cada elemento do vetor X.
Para isso vamos utilizar aquela sintaxe de vetores que antes da operação vamos escrever um pontinho (à direita do vetor X), sendo assim, a função fica:
Agora que já criamos os cálculos de todos os pontinhos da função, vamos chamar a função plot para imprimir o gráfico como uma variável de saída. Dentro do argumento da função plot escrevemos primeiro o vetor que nos dá as coordenadas do eixo horizontal (x), ou seja, as abscisas, e depois os valores da função no eixo vertical (y), ou seja, as ordenadas.
E finalizamos formatando os eixos do gráfico:
Passo 3
Implementando o código em Matlab temos a seguinte rotina:

Executando o código, o Matlab irá nos fornece o seguinte gráfico:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Elaboração Própria”
Construa em Matlab o gráfico da função dada e da sua derivada:
Sob o intervalo
Passo 1
A questão em si está querendo simplesmente imprimir os valores da função e da sua derivada sob a variação de X, mas não em forma de uma tabela e sim na forma gráfica em um único gráfico.
Para tirar a derivada basta utilizarmos as variáveis simbólicas para obter a derivada, uma vez que temos a derivada em mão, iremos para a criação do código precisamos criar o algoritmo para entender o que o código faz:
- Entrada de dados, aqui implementa o valor de X.
- Cálculo da função de X
- Plotagem da função
- Nomeando os eixos e o título do gráfico.
Passo 2
Primeiro passo é a obtenção da derivada, para isso no commad window vamos criar a variável simbólica X.
Uma vez que criamos a variável simbólica vamos implementar a função
Agora que implementamos a função simbólica vamos tirar a derivada da função
E iremos obter a seguinte função derivada:
Passo 3
Primeiro passo é a criação do vetor de entrada:
Uma vez que criamos o vetor vamos calcular os valores da função e sua derivada:
Iremos chamar o plot da função e sua derivada:
E finalizamos formatando os eixos do gráfico:
E para organizar melhor vamos colocar a legenda no gráfico:
Passo 4
Implementando o código no matlab ele fica da seguinte forma:

Executando o código podemos obter a seguinte curva:
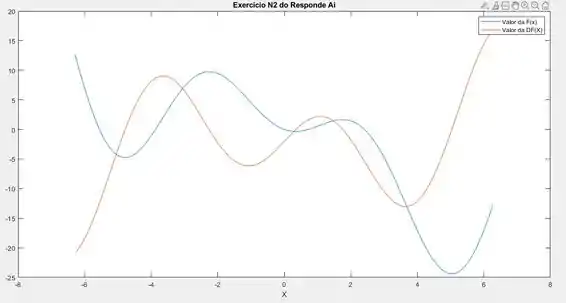
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
“Elaboração Própria”
Em um teste de tração de um corpo de prova, as extremidades da amostra são forçadas recebendo uma tensão mecânica.
Durante o ensaio, a força F necessária para distender a amostra de um comprimento L é medida através de um equipamento, o equipamento fornece os seguintes resultados:
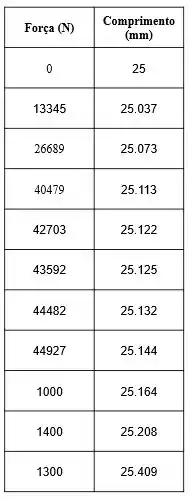
A amostra tem um raio de 6.4 mm, utilizando dessas informações plote a curva da tensão em função da deformação do material.
Dica: para isso utilize as seguintes equações para tensão e deformação respectivamente
Onde o L,A0 e F são respectivamente o comprimento, a área e a força aplicado no corpo.
Passo 1
A questão em si é um dos exemplos mais batidos para aqueles que atuam na engenharia, onde você consegue observar qual a deformação de um determinado material sob a ação de um campo de tensão.
Para isso utilizamos os dados experimentais obtidos pela máquina e utilizamos as equações que foram disponibilizadas no problema para o cálculo da tensão e da deformação do material.
Então o algoritmo se torna:
1-Implementação da entrada de dados, colocar os valores de
2-Cálculo da Área da amostra, da tensão e deformação
3-implementação do plot
4-formatação da curva.
Passo 2
Primeiro passo é a criação dos vetores de entrada no Si:
Cálculo da área, tensão e deformação no SI
Agora iremos chamar o plot da tensão em função da deformação
E finalizamos formatando os eixos do gráfico:
Passo 3
Implementando o código no matlab ele fica da seguinte forma:
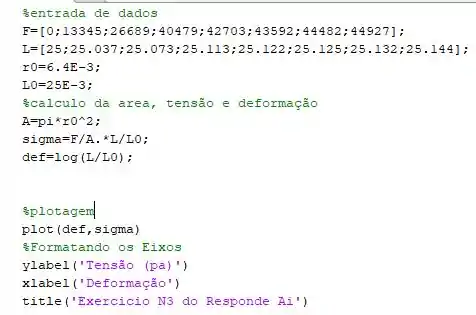
Executando o código podemos obter a seguinte curva:
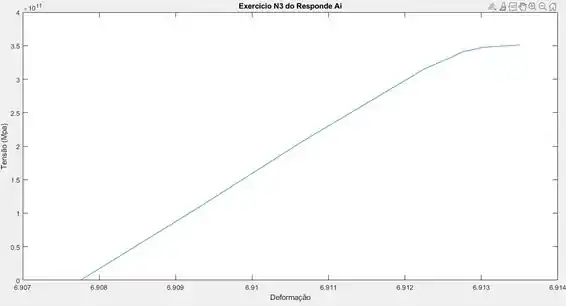
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
“Elaboração Própria”
A órbita dos planetas ao redor do sol pode ser modelada aproximadamente pela equação polar.
Os valores das constantes e para quatro planetas são mostradas abaixo:
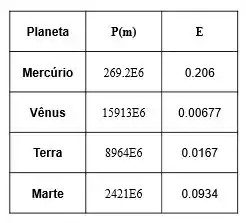
Plote as órbitas dos planetas apresentados em função de teta, todos em um único gráfico.
Passo 1
A questão em si pede para modelar as órbitas dos planetas Mercúrio, Vênus, Terra e Marte.
Onde a ideia é utilizar os dados fornecidos na questão e variar o ângulo teta de 0 até para assim calcular os valores dos raios de todas as órbitas e imprimir os resultados em uma curva bidimensional.
Então o algoritmo se torna:
1-Implementação da entrada de dados:
2-Cálculo dos raios
3-implementação do plot
4-formatação da curva.
Passo 2
Primeiro passo é a criação dos vetores de entrada no Si:
Cálculo dos raios dos planetas
Agora iremos chamar o plot da tensão em função da deformação
E finalizamos formatando os eixos do gráfico:
Passo 3
Executando o código podemos obter a seguinte curva:
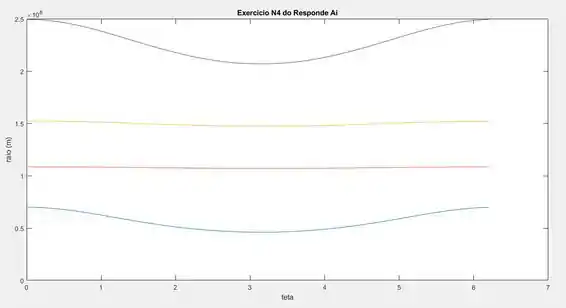
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
“Elaboração Própria”
Um resistor e um indutor são conectados em série com uma fonte de tensão. Quando a fonte de tensão produz pulsos regulares de amplitude 12 V e duração 0.5s.
A corrente do que passa no circuito é modelada pelas seguintes funções:
E
Plote em um único gráfico ambas as curvas para uma melhor visualização do comportamento físico do sistema.
Passo 1
A questão pede pra gente estudar a variação da corrente em um circuito RLC, a ideia aqui é estudar o que acontece com a corrente quando existe uma variação no tempo.
Porém, a função que modela a corrente muda conforme o tempo avança.
Sendo assim, o nosso plot irá possuir duas curvas. A primeira curva irá corresponder a corrente para valores de tempo até os 0.5 segundos.
Depois de 0.5 segundos iremos utilizar a segunda função e então iremos implementar uma segunda curva no mesmo gráfico.
Lembrando alguns detalhezinhos, o Matlab de certa forma ele não plota uma curva contínua, na realidade ele calcula a função que queremos em diversos pontinhos e gera um gráfico com esses pontinhos um do lado do outro. Quando esse gráfico aparece na nossa tela do computador, esses pontinhos ficam tão próximos um do outro que dá a impressão que é uma curva contínua. Na verdade, a gente plota vetores com pontos da função e não a própria função!
Então para os pontos ficarem pertinhos um do outro e melhorar nossa precisão, geralmente, se define os incrementos na ordem de 0.01.
Então precisamos indicar quais são esses pontos onde a função irá calcular o seu valor, belezinha?
Sendo assim, o algoritmo da rotina vai ser da seguinte forma:
1-Entrada de dados: V,R e L
2- Cálculo da função
t1=0:0.01:0.5
t2=0.5:0.01:1
Cálculo da função i1
Cálculo da função i2
3-Implementação do gráfico
4-formatação da curva
Passo 2
Como mostra no algoritmo, primeiramente devemos criar os dados de entrada.
E criar os vetores de tempo.
Calculando os valores das correntes:
Agora iremos fazer o plot da corrente em função do tempo, como nós temos dois vetores de tempo e dois vetores de corrente para plotar precisamos indicar os pares na ordem correta.
Como os valores da função corresponde aos valores do vetor temos que a função plot fica:
Agora precisamos indicar os pares correspondente a segunda curva que irá aparecer no gráfico, para isso vamos utilizar os pares e seus valores de correspondente e só precisamos fazer a seguinte modificação no plot:
E lembrando sempre, primeiramente se colocar os valores do eixo X que nesse caso é o tempo, depois coloca-se os valores do eixo Y que nesse caso é os valores das correntes, belezinha?
E agora finalizamos formatando os eixos do gráfico:
Passo 3
Executando o código podemos obter a seguinte curva:
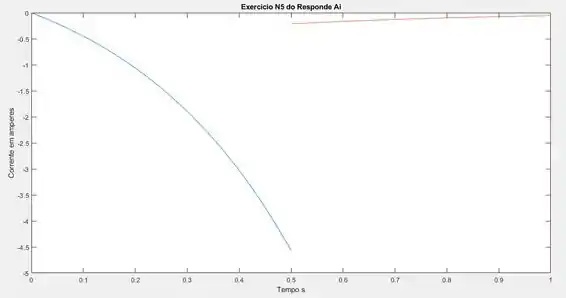
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Adaptada de Matlab com aplicações em engenharia - Amos Gilat - Questão 4 - Página 150
Esboce o gráfico seguinte função:
No intervalo
Perceba que a função é descontínua em . Plote a função criando dois vetores no domínio O primeiro vetor terá elementos de até e o segundo vetor terá elementos de até
Passo 1
Opa galerinha, essa é uma questão típica de função bidimensional. Aqui nós temos uma variável dependente que é o em função de uma variável independente que é o , caracterizando uma curva bidimensional no Matlab.
Para gerar uma curva desse tipo utilizamos a função que é a função responsável por imprimir uma saída de dados gráfica.
Só que para utilizá-la iremos precisar de no mínimo dois vetores. Um vetor que corresponde ao eixo das ordenadas e segundamente vamos precisar de um vetor que será o eixo das abscissas.
Porém, essa questão aqui tem uma limitação. Essa função não está definida para valores de pois, analisando a função vemos que aparece uma divisão por 0 gerando assim uma indeterminação.
Para fugir desse problema vamos dividir o intervalo grande que é de até em dois intervalos pequenos excluindo o para assim remover a indeterminação.
Os valores de incrementos podem ser escolhidos de forma arbitrária eu irei utilizar 0,01 mas você pode utilizar qualquer um, certo?
Sendo assim, nosso algoritmo fica:
1-Criação do vetor x1,
2-Criação do vetor x2,
3-Cálculo do vetor y1,
4-Cálculo do vetor y2,
5-Plotagem da curva.
Passo 2
Agora que criamos o algoritmo basta transformá-lo em um programinha do Matlab, as primeiras linhas de código são apenas as criações dos vetores, logo:
Agora vamos criar os vetores calculando as funções nesses intervalos, lembre-se que estamos realizando o cálculo da função em cada elemento do vetor , então precisamos colocar o antes da operação para indicar isso.
Até aqui tá tudo okay, agora vamos para a novidade.
Passo 3
A função plot precisa de dois argumentos, o primeiro argumento é o eixo das abscissas e o segundo argumento é o eixo das ordenadas. Ou seja, sempre que for plotar precisamos colocar no primeiro argumento o vetor que corresponde os valores de e depois os valores do eixo .
Porém temos dois gráficos, né?
Então para inserir o segundo gráfico basta continuar, primeiro inserimos os valores do eixo x do segundo gráfico e depois inserimos os valores do eixo y do segundo gráfico.
Inserindo tudo certinho seu código deve ficar assim:
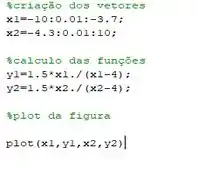
O executando sua curva deve ficar algo mais ou menos assim:
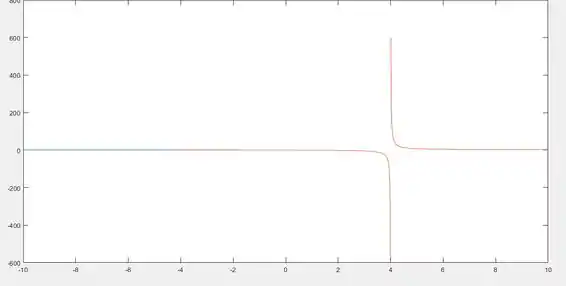
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Adaptada de Matlab com aplicações em engenharia - Amos Gilat - Questão 17 - Página 154
Uma viga em balanço em engenharia é definida como uma barra de concreto que tem uma extremidade chumbada em uma parede enquanto a outra está livre.
Aplicando uma força uniforme sobre toda a viga de intensidade , temos que a deflexão em um determinado ponto é dada pela seguinte equação:
Onde é uma constante chamada de módulo de elasticidade, é o momento de inércia e é o comprimento da barra, como mostrado na figura abaixo:

Considere uma viga de alumínio com os seguintes dados:
Plote um gráfico da deflexão da viga em função do .
Passo 1
Opa galerinha aqui estamos em um problema de curva bidimensional de um problema de deflexão, a deflexão é um dos maiores problemas mecânicos na engenharia pois ela é um dos primeiros indícios de que o material está propício a alguma falha mecânica.
Na linguagem popular a deflexão tem o nome de “invergar”, continuando a resolução do problema...
Um problema de uma curva bidimensional é configurado quando queremos plotar uma curva onde nós temos uma variável dependente e uma única variável independente.
Para realizar o plot de uma curva bidimensional precisamos apenas da função e para executar essa função precisamos de dois argumentos vetoriais.
O primeiro argumento é o eixo das abscissas que nós chamamos de eixo na matemática e segundamente precisamos dos eixos das ordenadas que comumente é chamado de eixo .
Aqui o nosso eixo será o comprimento da viga e será um vetor que irá variar de 0 até 6m com uma variação de 0.01 que pode ser escolhido de forma arbitrária.
O segundo vetor que é o eixo , será a deflexão que iremos criar a partir do cálculo da função em cada elemento do vetor
Belezinha? Então vamos escrever nosso algoritmo:
1-Entrada de dados-
2-Criação do vetor
3-Cálculo da função
4-Plotagem do gráfico e organização do mesmo.
Passo 2
Agora que montamos o algoritmo vamos implementá-lo no Matlab.
Primeiramente vamos gerar a nossa entrada de dados:
;
;
;
Agora vamos criar o nosso vetor
;
Agora vamos calcular os valores da função em cada elemento do vetor , okay?
Lembrando como estamos realizando uma operação vetorial elemento a elemento precisamos indicar isso colocando o “.” antes de cada operação aritmética.
;
Agora que criamos os vetores e precisamos plotar a função apenas.
Para plotar precisamos apenas chamar a função plot, porém devemos lembrar de um detalhe.
O primeiro argumento é o eixo das abscissas, logo ele é o vetor por ela ser a variável independente.
O segundo argumento é o eixo das ordenadas, representado pelo vetor , que é nossa variável dependente.
Agora já temos o plot, mas ele fica melhor se indicarmos o que é cada letra né?
Para isso, vamos nomear os eixos e iremos precisar de duas funções. A função e a outra se chama a
Para nomear os eixos precisa apenas fazer o seguinte procedimento:
)
Ou seja, precisamos apenas chamar a função, colocar o igual e escrever entre aspas simples o nome do eixo. Na realidade estamos anexando um string aos eixos.
Nesse caso são os strings: comprimento da viga e deflexão da viga.
Escrevendo tudo certinho seu código deve ficar assim:

Executando o código, deve aparecer algo mais ou menos assim:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Adaptada de Matlab com aplicações em engenharia - Amos Gilat - Questão 19 - Página 155
O limite de escoamento é uma propriedade dos materiais que define o valor máximo de uma determinada pressão na qual o material apresenta características de uma falha.
Em geral ele é função de diversos parâmetros inclusive a taxa com que o material se deforma (alonga, enverga, comprime e etc.).
Os dados a seguir dão o limite de escoamento de um certo tipo de aço em várias taxas de deformação:
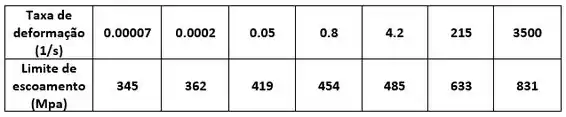
Estudiosos geraram a seguinte equação para modelar o limite de escoamento desse material:
Plote os dados experimentais e também a equação que os estudiosos descobriram e responda se a equação realmente reproduz os dados experimentais.
Obs: em vez de usar a função , use uma a função a sintaxe é idêntica a diferença é que a função plota o eixo dos todos em escala logarítmica deixando a visualização nesse caso melhor.
Passo 1
Opa galerinha aqui estamos em um problema de curva bidimensional, a ideia aqui é plotar tanto a curva quanto os pontos experimentais para ver se a equação realmente se aproxima dos dados experimentais.
Um problema de uma curva bidimensional é configurado quando queremos plotar uma curva onde nós temos uma variável dependente e uma única variável independente.
No nosso caso a variável dependente é o limite de escoamento enquanto a independente é a taxa de deformação.
Para realizar o plot de uma curva bidimensional em escala logarítmica precisamos apenas da função e para executar essa função precisamos de dois argumentos vetoriais.
O primeiro argumento é o eixo das abscissas que aqui será a taxa de deformação e o segundo argumento é o eixo das ordenadas que é o limite de escoamento.
A função ela vai imprimir os dados em um gráfico similar a função , porém irá ajustar o eixo para que possamos ter uma melhor visualização, o deixando em escala logarítmica.
Para comprar as visualizações, vamos tanto gerar o gráfico pela função , quanto pela função
Como vamos plotar tanto os dados experimentais quanto a função em um mesmo gráfico para compará-los, para o cálculo da função iremos precisar criar um vetor taxa de deformação.
Esse vetor ela irá variar de 0.000007 até 3500, como aqui temos muitos pontos iremos colocar uma variação de 1 arbitrariamente, você pode colocar qualquer valor que achar melhor.
O segundo vetor que é o limite de escoamento será criado a partir da função calculada no vetor taxa de deformação.
Uffa, Belezinha? Então vamos escrever nosso algoritmo:
1-Implementação dos dados experimentais
2-Criação do vetor taxa de deformação
3-cálculo da função limite de escoamento sigma
4-Plotagem dos gráficos e organização do mesmo.
Passo 2
Agora que criamos o algoritmo basta apenas transformá-lo em um código.
Primeiramente vamos implementar os vetores com os dados experimentais:
Vamos chamar a taxa de deformação experimental de e a tensão de escoamento experimental de .
Agora que inserimos os dados experimentais vamos calcular as funções, para isso vamos primeiro criar um vetor auxiliar taxa de deformação para o cálculo da função sigma:
Lembrando de colocar o “.” Antes da operação de potenciação pois estamos aplicando a função a cada elemento do vetor .
Agora que criamos todos os vetores, precisamos apenas criar os plot.
Primeiramente vamos criar o plot usando a função , lembrando que precisamos de dois argumentos para a função plot.
Primeiramente o eixo das abscissas e depois os eixos das ordenadas:
Agora vamos plotar também as funções nesse mesmo gráfico e para isso preciso apenas inserir novamente as variáveis dentro do mesmo plot.
Para deixar o gráfico de uma forma organizada vamos inserir algumas legendas nele junto com a nomeação dos eixos.
Primeiramente vamos nomear os eixos, utilizando as funções e, a sua sintaxe é a seguinte
Precisamos apenas escrever o texto dos eixos dentro de parênteses e aspas simples.
Assim, estamos imprimindo nos gráficos os nomes dos eixos.
Como nós temos duas curvas em um mesmo gráfico ficaria legal nomeá-las, né?
Para isso vamos utilizar a função e sua sintaxe é o seguinte:
Apenas chamar a função e colocar entre parênteses os nomes das curvas, o primeiro nome ela automaticamente vai associar aos dois primeiros argumentos da função e o segundo nome aos segundos argumentos da função
E para indicar qual é, é só inserir na ordem e separar os nomes com uma vírgula simples.
Uffa, se digitou tudo certinho finalmente o seu código deve estar mais ou menos assim:

Executando o código iremos gerar a seguinte função:

Passo 3
A exibição ficou horrível né? Sabe porquê?
A resposta é a seguinte, os primeiros pontos são bem próximos, mas se você analisar os últimos pontos são muitos distantes e isso prejudica a visualização do plot.
A escala logarítmica surge para meio que ajustar o eixo X e você analisar melhor a plotagem.
Então vamos fazer o seguinte, apaga a palavra no código e coloca e o resto permanece intacto, logo o seu código ficará assim:
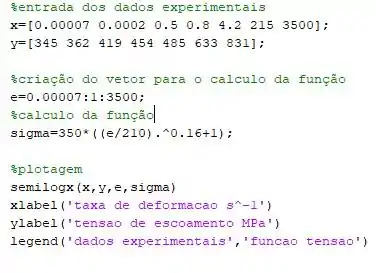
E se você executar esse seu código aparecerá o seguinte plot:

Bem melhor de visualizar né?
Sabe o que fizemos? Apenas olhe o eixo do gráfico.
Isso ae, modificamos a escala do gráfico e agora conseguimos ver que o modelo se aproxima relativamente bem dos dados experimentais.
Pois nenhum modelo teórico irá se aproximar 100% dos dados experimentais.
Resposta
Ei, a resposta está no passo a passo :)