Interação, Ramificação e controle de fluxo 2(Estruturas de repetição)
Teoria
O que é essas estruturas de repetição?
Opa, eae tudo bem?
Hoje vamos conversar sobre as estruturas de repetição, mas o que é isso né?
Vamos supor que você foi ao supermercado comprar umas 10 frutas. A gente tá tão acostumado a fazer isso sempre que já nem pensa mais no processo, mas se olharmos direitinho, existe uma sequência de passos que seguimos para selecionar as frutas, que pode ser escrita como um algoritmo:
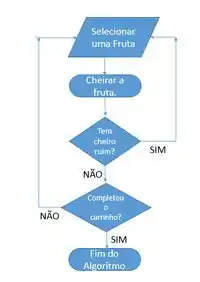
Analisando o algoritmo, você começa sempre selecionando uma fruta e executa “a função” para verificar se a fruta está apropriada para consumo ou não através do seu cheiro. Depois, dependendo do resultado, você devolve a fruta e pega outra ou coloca a fruta no carrinho pra levar.
Depois de encontrar uma fruta boa, você verifica quantas frutas já tem no carrinho, se tiver menos do que você deseja, você refaz o passo a passo novamente do começo até completar as 10 frutas no carrinho.
Em programação, esse processo que você está fazendo ao comprar uma fruta de ficar pegando fruta após fruta até completar seu carrinho recebe um nome específico, é uma estrutura ou laço de repetição.
A ideia aqui é você pegar seu algoritmo ou um trecho do seu algoritmo, e fazer ele se repetir infinitamente até que um certo critério seja completado, no caso do exemplo seria colocar as 10 frutas no carrinho. Esse critério recebe um nome específico na programação também que é chamado de critério de parada.
No Matlab existem duas funções para montar essas estruturas de repetição: uma delas é chamada de função for e a segunda função é chamada de while.
A diferença fundamental entre elas é que o for é utilizado apenas quando os critérios de paradas são finitos, enquanto o while pode ser utilizado com critérios de parada infinitos e finitos.
Por exemplo: no nosso exemplo você vai no mercado comprar 10 frutas, sendo assim seu laço irá se romper quando você completar as 10 frutas, logo o critério de parada é finito, podendo utilizar tanto o for quanto o while para montar um laço desse tipo.
Agora que já falamos da ideia, vamos praticar um pouco no Matlab?
Função For
Bem, mesmo com a limitação do for de apenas ser utilizado em casos com critérios de paradas finitos ele é mais utilizado que o while, muitas vezes por sua simplicidade e também porque é muito incomum em sistemas de engenharia cair problemas na qual precise de um critério de parada infinito.
Para entendermos a sintaxe vamos fazer um exemplo simples, vamos somar todos os 10 primeiros números que existem de a .
O algoritmo é algo assim:
- Partimos de um valor inicial que é o
- Vamos somar o valor anterior mais o valor seguinte
- O critério de parada é somar o número
Agora vamos escrever no Matlab:
Pra começar, vamos indicar o valor inicial da soma criando uma variável:
Depois, vamos chamar a função for:
Aqui chamamos a função . Para isso, criamos uma nova variável que vai definir o critério de parada, seu valor inicial será e vamos incrementar de um em um até que chegue ao , quando o laço vai encerrar.
Depois disso vamos colocar o código, que será repetido. Já definimos que a soma irá começar do , então a cada ciclo de repetição vamos somar a essa variável o valor de , que vai iniciar em e ir até , completando a tarefa que queremos. Então a função ficará algo mais ou menos assim:
E finalizaremos com end, e após isso podemos colocar a saída de dados.
O código vai fazer o seguinte:
- Quando o
- Quando o , temos
- Quando , temos
- é a variável de controle do laço (também conhecida como índice do laço);
- é a expressão de controle do laço, que irá executar o bloco de códigos igual ao número máximo de vezes que se pedir, que no exemplo anterior foi .
E assim sucessivamente. Inserindo o código no Matlab e rodando temos:
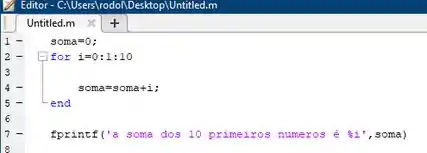
Se executarmos o código, o Matlab agora irá calcular o valor da soma dos 10 primeiros números:
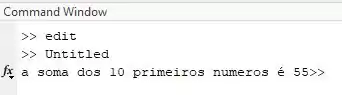
Então de uma forma geral a sintaxe do for pode ser vista da seguinte forma:
Onde
A ideia aqui é que o será um vetor que conta quantas vezes o laço irá se repetir. A expressão de controle começa de um valor inicial e vai até a um valor final, executando o de código e somando um incremento definido pelo programador.
A sintaxe é a seguinte:
Função While
Diferente do for que repete o laço uma quantidade definida de vezes imposta pelo programador, o while repete a estrutura até uma condição ser satisfeita, independente de quantas vezes seja necessário rodar o código até que isso aconteça.
Essa condição pode ser colocada no while de duas formas, vamos utilizar o exemplo anterior para explicitar a primeira forma.
Começamos o código no Matlab com as seguintes linhas, declarando as variáveis:
Aqui usamos as mesmas variáveis do caso anterior, incluindo o valor inicial da expressão de controle, uma vez que o while também vai precisar dela.
Na segunda linha colocamos:
Aqui começamos a linha do código com a expressão while, porém a expressão de controle é trocada por um teste lógico, e sempre que esse teste não for respeitado o laço se repete.
Então, vamos ao objetivo do nosso programa, que é somar os números de a :
No bloco de comando temos que adicionar uma informação a mais, que é como a expressão de controle se atualiza conforme o laço se repita:
Esse passo é muito importante na função while, sem ele nosso programa não atualizará o valor de , então iremos somar sempre o valor inicial e o laço nunca terminaria, já que a condição nunca seria atendida.
Finalizamos com o end para fechar o laço e depois com uma saída de dados.
O código em Matlab fica assim:
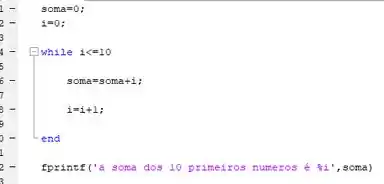
Existe uma segunda forma de encerrar o laço de repetição, por exemplo se queremos somar números até a soma ser igual a .
Para isso, precisaremos da função break, que serve para cancelar o laço antes do critério de parada ser atendido. Então dentro do código anterior aumentaremos o número de termos de para e colocaremos o seguinte teste lógico:
Ou seja, se a soma for igual ou maior que , o laço se encerra. Seu código deve ficar mais ou menos assim:
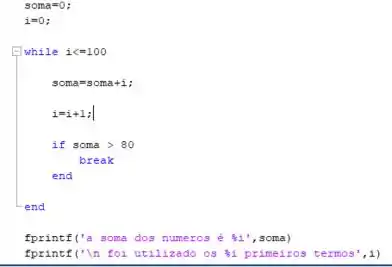
Onde o código ao se executar irá mostrar o valor da soma e também quantas vezes o laço somou através da nova saída de dados colocada no código.
Bem, sei que na teoria parece até complicadooo, porém com a prática essas coisas vão ficando mais claras na cabeça. Então não esqueça de ir olhar os exercícios que selecionamos para você, belezinha? Então até maissssss!
Função For
Função While
Exercícios Resolvidos
Exercício Resolvido #1
“Elaboração Própria”
- Examine o laço a seguir e determine o valor em ires.
Ires = 0
for index = 1:1:10
Ires = Ires + Index*2
end
Passo 1
A ideia aqui é entender a estrutura do laço, então precisamos desenvolver o laço e para isso saber o valor final da variável Ires quando o laço acabar.
Aqui podemos resolver de duas formas: primeiramente resolver manual para entender a estrutura do laço, e depois disso utilizar o Matlab para ver o valor final.
Passo 2
O for cria um loop e a variável index vai ser uma espécie de contador, que vai assumir diferentes valores a cada volta no loop e vai ajudar a dizer quando tem que parar.
Quando a gente escreve , a gente tem 3 valores numéricos depois do sinal de igual. O primeiro é o valor inicial da variável index, então quer dizer que na primeira iteração . O segundo é o incremento adicionado à variável index a cada iteração, ou seja, a cada volta somamos 1 ao valor do index. E o terceiro número é quando temos que parar. Quando , o loop para.
Resumindo, a variável index assume valores 1, 2, 3, 4... e por aí vai até 10!
Passo 3
Agora que entendemos o loop, vamos fazer os cálculos.
Inicialmente
Entrando no laço temos, na primeira iteração:
Index =1
Ires=0
Então o novo valor de Ires é:
Na segunda iteração, temos:
Index = 2
Ires = 2
Então o novo valor de Ires é:
E assim sucessivamente, logo a ideia é que o valor seguinte do ires é o valor anterior somado com 2 vezes o index.
Implementado no Matlab, podemos ter cada valor de index a cada ciclo de repetição como mostrado no codigozinho abaixo:
Resposta
Executando o codigozinho temos um valor final para ires=110.
Exercício Resolvido #2
“Elaboração Própria”
Examine os laços for abaixo e determine quantas vezes cada laço será executado e qual o valor final impresso da variável de controle.
a) for I = 7:1:10
b) for J = 7:-1:10
c) for J = 1:10:10
d) for ii = -10:3:-7
Passo 1
Para estudar os laços precisa saber que a sintaxe equivale a:
Valor inicial: incremento: Valor final
Sendo assim para estudar cada alternativa precisamos começar do valor inicial e ver quantos grupos de incrementos cabe até alcançar o valor final
Passo 2
- Na primeira alternativa vemos que o laço começa de 7 e varia de 1 em 1 até chegar até o 10, totalizando 3 incrementos logo teremos 3 ciclos de repetição
- Aqui o J começa em 7 e vai até 10, variando de -1, como vemos isso não é possível logo o laço nunca chegará em um final logo não irá executar.
- Nesse aqui temos o J que irá começar do 1 e irá até o 10 com um incremento de 10, então do 1 até 10 temos apenas 1 incremento de 10, logo o ciclo irá se executar 1 vez.
- Nessa alternativa começamos no -10 então o laço irá executar até chegar em -7 variando de 3, logo teremos um incremento de 3, chegando em -7. Sendo assim o laço executa uma vez.
Resposta
- irá executar 3 vezes
b) não executa
c) irá executar 1 vez
d) irá executar 1 vez
Exercício Resolvido #3
“UTFPR – Algoritimos – P2 – 2017.1”
Suponha que seja o número de Fibonacci na posição n. Elabore um código que calcule o valor da sequência de Fibonacci.
Passo 1
Opa iae, está tudo bem?
A questão em si é um problema que pede a elaboração de um programa que calcule o termo que se pede da sequência de fibonacci, para o cálculo da sequência precisamos lembrar da equação de recorrência da sequência de Fibonacci que é:
Porém nós só temos os termos de e os termos de então trocando n por i+3 temos que:
Porém ao fazer esse ajuste o intervalo de variação vai do 0 até o N-3 requerido, pois somamos i+1 nos índices.
Além disso, precisa saber que os dois primeiros números da sequência equivalem a 0 e 1 respectivamente.
Passo 2
Para programar precisamos primeiramente inserir as entradas de dados.
N=input(‘Digite termo N na qual se deseja descobrir o valor da sequência = ’)
Uma vez que já colocamos a entrada de dados precisamos programar a estrutura de repetição
F(1)=0;
F(2)=1;
For i=0:1:N-3
F(i+3)=F(i+1)+F(i+2)
End
Uma vez que já programamos a estrutura de repetição, precisamos apenas programar a saída de dados.
Fprintf(‘O valor da sequência F(%i) é dado por %f’,N,F(N))
Passo 3
Após a implementação do código teremos algo mais ou menos assim:
Executando o código podemos na janela command Windows teremos o seguinte resultado:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
“Elaboração Própria”
Escreva uma Rotina em Matlab para calcular o valor de A. A expressão que define A é dada por:
Passo 1
Opa iae, está tudo bem?
A questão é que ela pede que elabore um programa que sirva para calcular um certo número A.
Primeiramente para obter uma melhor visualização do problema é mais simples trabalhar com notação inicial, por exemplo se analisarmos bem podemos ver que a expressão de A equivale a seguinte expressão:
Ou seja, para um dado valor de N, podemos obter uma aproximação para o valor de A, comumente se escolhe um grande valor de N para que A se aproxime cada vez mais do seu valor verdadeiro.
Passo 2
Para o início do cálculo precisaremos começar pela entrada de dados:
disp(‘Digite um grande valor de N’)
N=input(‘digite o valor de N para aproximar o A =’)
Agora precisaremos implementar a estrutura de repetição, para isso vamos fazer variar a expressão de controle de 0 até o termo N, então temos:
Soma=1
For i=0:1:N
Soma=Soma+1
End
Uma vez que criamos o laço de repetição precisamos apenas criar a saída de dados
Fprintf(‘o Valor de A equivale a %f com uma aproximação de ordem %i’,Soma,N)
Passo 3
Após a implementação do código teremos algo mais ou menos assim:
Executando o código podemos na janela command Windows teremos o seguinte resultado:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
“Elaboração Própria”
Escreva uma codificação em Matlab capaz de avaliar os valores da seguinte expansão de Maclaurin e além disso revele o erro entre a utilização da expansão e da própria exponencial.
Passo 1
Opa iae, está tudo bem?
A questão pede para elaborar um programa que calcule uma soma em séries de potência da exponencial. No caso aqui nós teremos duas entradas de dados.
A primeira entrada de dados corresponde ao número de termos que o somatório tem, no caso o , e a segunda entrada de dados é o valor de pelo qual se quer aproximar o valor da exponencial.
Porém o código deve conter uma advertência, as séries de Maclaurin foram criadas para cálculo de funções em torno da origem, ou seja, quanto mais se distanciar da origem maior será o erro.
Para elaboração desse algoritmo precisamos da função fatorial do Matlab, que sua sintaxe corresponde ao
Passo 2
Para o início do cálculo precisaremos começar pela entrada de dados:
Agora precisaremos implementar a estrutura de repetição. Para isso vamos fazer variar a expressão de controle (que é a variável que aparece ali do lado do ) de 0 até o termo N, pois o somatório acontece de 0 até N e nós vamos usar o na nossa conta. Então temos:
E repara que ali dentro do , eu já coloquei o cálculo da soma, que vai sendo alterado a cada volta, de 0 a N.
Passo 3
Uma vez que criamos o laço de repetição precisamos apenas criar a saída de dados
Além do valor da soma, vamos também criar o valor erro
Passo 4
Após a implementação do código teremos algo mais ou menos assim:
Executando o código podemos na janela command Windows teremos o seguinte resultado:
Então vemos ali na última linha que o erro é tão pequeno que o matlab aproxima pra zero.
Resposta
O erro é zero.
Exercício Resolvido #6
Adaptada da Questão 11 - Matlab com aplicações em Engenharia – Amos Gilat – página 218
Escreva um programa (usando os laços) que determine a soma dos primeiros termos da série.
Rode o programa com m=10 e depois com m=500.
Compare o resultado encontrado com o resultado analítico dessa soma com infinitos termos que é .
Passo 1
Opa galera, aqui temos um exercício que é laços de repetição.
Porque é um laço de repetição né?
Pelo motivo que vamos pegar a função dada no enunciado e vamos atribuir valores da seguinte forma:
E vamos conversar né? Realizar isso 50 vezes ou 500 vezes não é nada legal de se fazer.
Por isso que vamos utilizar dos laços de repetição, para assim poder realizar essa soma diversas vezes com poucas linhas de código.
Uma vez que implementamos os laços de repetição vamos comparar a soma com 50 termos desse e outra soma com 500 termos com a solução se fizéssemos infinitas vezes que é .
Sendo assim o algoritmo se comporta em 3 passos:
1-Implementação do valor de m
2-realização das estruturas de repetição
3-Análise final do resultado.
Passo 2
Agora que sabemos o que fazer primeiramente vamos implementar o número máximo da soma que vamos chamar de m, assim como a questão instruiu.
Agora vamos inserir o primeiro valor da soma, como nossa soma vai começar o então vamos colocar o elemento neutro da soma que é o 0.
Sendo assim vou dizer que a soma é:
Agora vamos criar o laço de repetição, para isso vamos utilizar a função for.
Onde o for depende de 3 argumentos, o primeiro é o valor inicial que vamos dizer que ele vai partir do ponto 1, o segundo argumento é a variação a cada repetição que também vai ser 1 e vamos finalizar com o número máximo de repetição que vai ser m.
Então o for ele vai ficar algo assim:
Inserindo a função disponibilizada na questão temos que:
Se você escreveu tudo certinho o código deve ficar mais ou menos assim:
Passo 3
Executando o código com m=50 temos:
Se executarmos o código com m=500 temos:
O valor de
Logo conseguimos perceber que se aumentarmos o número de termos na soma mais próximo do valor analítico ela se aproxima.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Autoria própria
Faça um programa que leia um valor n, inteiro e positivo, calcule e mostre a seguinte soma:
Passo 1
Opa pessoal, tudo bem?
Aqui temos um exercício de laços de repetição, basicamente o exercício pele para que criemos um programinha que a partir de um valor qualquer que vamos inserir a partir do teclado ele realize a soma que foi disponibilizada no exercício.
Bem, para pequenos valores isso não gera problema em resolver na mão.
Por exemplo se n for igual a 2 temos que:
Mas se n for igual a 1000? As coisas complicam muito né?
É aí que o Matlab surge como salvador, um simples código de estruturas de repetição com entradas e saídas de dados resolve esse probleminha cavernoso.
Para resolver o problema vamos precisar de uma entrada de dados para inserir o valor de n a partir do teclado e a função do Matlab que faz isso é a função
Após isso vamos precisar criar uma estrutura de repetição para realizar todas as somas até chegar no valor de .
E para finalizar vamos precisar de uma saída de dados para imprimir o valor da soma e para isso vamos utilizar a função para imprimir a saída de dados.
Sendo assim, o algoritmo do problema se torna:
1-Entrada de dados- implementação do valor de n
2-Início do laço
2.1 – Programação da função.
2.3 – Finalização do laço.
3 – Saída de dados.
Passo 2
Agora que criamos o algoritmo vamos implementar nosso código e para isso vamos começar com a entrada de dados.
Na entrada de dados devemos chamar a função input para que possamos ler valores de entrada de dados diretamente do teclado.
A sintaxe da função input é sempre essa que está descrita, vamos chamar alguma variável e anexar a ela a função input.
Dentro de parênteses simples, escrever um textinho para melhor orientar a pessoa na hora de escrever e deixar o código mais organizado.
Um detalhezinho, como podemos ver na nossa questão o primeiro valor da nossa soma é sempre 1.
Logo vamos colocar o primeiro valor fora do laço, belezinha?
Fazemos isso para ficar mais fácil de criar o laço porque podemos realizar sempre dessa forma que vamos fazer agora.
No nosso laço de repetição, como nos colocamos o primeiro termo da soma fora do laço vamos começar o iterador do a partir do 2.
Porque olha a função:
Depois do primeiro termo o segundo termo começa com
Sendo assim, o vai ficar:
Agora vamos implementar a função, aqui temos um detalhe.
Sempre que o for atualizar queremos que ele pegue o valor anterior e some o novo para que assim ele realize a soma, bele?
Olha só se o n=2 temos a seguinte soma:
Quando o n=3 temos que:
Substituindo o em temos:
Ou seja:
Agora vamos implementar a saída de dados utilizando a função
Cuja a sintaxe é essa apresentada, precisamos apenas chamar a função e escrever algum textinho para deixar mais organizada a saída de dados.
No local onde iremos colocar o vamos imprimir o valor da soma, depois de escrever o texto entre aspas simples precisamos indicar que aquele se trata da variável soma por isso colocamos depois o nome soma.
Se você digitou todo seu código certinho deve gerar um código mais ou menos assim:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Autoria própria
Elabore um programa que receba dois números inteiros e gere os números inteiros que estão no intervalo compreendido por eles.
Passo 1
Opa galera, tá tudo em cima?
Aqui temos um exercício de laços de repetição, basicamente o exercício quer que você elabore um programa que dado dois números inteiros imprima todos os números inteiros entre eles.
No matlab existem diversas formas de resolver esse problema, porém, aqui vamos utilizar os laços de repetição.
Para resolução desses exercícios vamos precisar primeiramente de dois elementos, esses elementos são os números que correspondem aos extremos do intervalo que vamos imprimir.
Esses números devem ser fornecidos pelo usuario do programa, ou seja, precisamos de uma função de entrada de dados e para isso vamos utilizar a função .
Após a entrada de dados vamos colocar um apenas para informar o que o programinha irá fazer e vamos escrever as estruturas de repetição.
Basicamente o nosso algoritmo se torna:
1-Entrada de dados
2-Função printf apenas para indicar o que o programa irá fazer
3-Estrutura de repetição.
Passo 2
Agora que criamos o algoritmo vamos implementar nosso código e para isso vamos começar com a entrada de dados.
Na entrada de dados devemos chamar a função input para que possamos ler valores de entrada de dados diretamente do teclado.
A sintaxe da função input é sempre essa que está descrita, vamos chamar alguma variável e anexar a ela a função input.
Dentro de parênteses simples, escrever um textinho para melhor orientar a pessoa na hora de escrever e deixar o código mais organizado.
Agora que implementamos a entrada de dados vamos chamar a estrutura de repetição.
Vamos analisar nosso probleminha, a partir de um valor de entrada nós queremos imprimir todos os valores até chegar em .
Sendo assim, se e temos que imprimir os números:
Se analisarmos bem podemos perceber que a estrutura de repetição já faz isso.
Portanto nosso laço irá começar de e vai variar de em até chegar no , gerando o seguinte
E o que precisamos imprimir é justamente os valores de que o for vai calcular, gerando a seguinte função:
Sendo assim, seu código deve ficar algo mais ou menos assim:
Ahh o fprintf ele entra ali apenas como um textinho para dizer o que o programa vai fazer.
Sua sintaxe é daquela forma, chamamos a função fprintf e escrevemos o texto entre aspas simples.
Resposta
Ei, a resposta está no passo a passo :)