Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Testes Lógicos (If, Else, Elseif e Switch Case)

Ver Todos os Exercícios

Teoria

Uma introdução básica...

Opa, iae está tudo bem?

Hoje vamos bater um papo sobre os testes lógicos, mas o que são os testes lógicos né?

Bem, vamos imaginar que você precisa ir ao mercado comprar algumas frutas e pra isso, sem perceber, você sempre irá aproximadamente executar um conjunto de atividades até completar a tarefa que é comprar as frutas.

Essas tarefas estão representadas nesse algoritmo abaixo:

Se analisar o algoritmo bem, você percebe que existem dois blocos cujas respostas são sim ou não.

O processamento desses blocos são perguntas, eles recebem uma informação vinda de um bloco anterior, e com essa informação realizam uma pergunta em relação à informação e tomam uma decisão direcionando a informação para o bloco seguinte.

Essa pergunta recebe o nome de teste lógico, nesse exemplo, se a fruta tiver um cheiro ruim seu cérebro processa a informação de pegar outra fruta, mas se a fruta tiver um cheiro agradável, o seu cérebro diz que ela está boa e coloca a fruta no carrinho.

Em síntese, um teste lógico redireciona o fluxo de informação do código para um determinado lugar a depender se sua resposta for SIM ou NÃO.

Mas... como coloco isso no Matlab né?

Calma, calma que iremos ver isso tudinho aqui nos mínimos detalhes!

Funções If e Else

Então basicamente temos três grandes funções que faz esse trabalho de perguntar algo, duas delas estão conjugadas que são as funções if e else outra bastante comum é a switch case.

Vamos primeiramente conversar sobre a if e else, traduzindo para o português a função if é o mesmo que se e a função else é o equivalente ao advérbio mas.

Então sempre que você for fazer um teste lógico deve pensar assim:

Se “a pergunta for sim”

Faça alguma ação

Mas “se a pergunta for Não”

Faça alguma ação

Fim

Logo levando para o algoritmo de comprar uma fruta no supermercado nós executamos o seguinte teste lógico:

Teste lógico: A fruta tem um cheiro ruim?

Se a resposta for “sim”

Coloque a fruta no lugar e selecione outra.

Mas se a resposta for “não”

Coloque a fruta no carrinho.

Fim

Levando para linguagem de programação a sintaxe ficaria:

If “SIM”

Selecionar outra fruta

Else

Colocar no Carrinho

end

Vamos realizar um exemplo no Matlab:

Vamos escrever um código que dá um número e informa se ele é par ou ímpar.

Para isso, vamos utilizar a função mod do Matlab, pois ela calcula o resto da divisão entre dois números, então para ser par a divisão por 2 precisa resultar um 0, então a função do teste lógico fica:

X = m o d ( d i v i d e n d o , 2 )

Então montando o algoritmo do problema se torna:

Então escrevendo na aba new script o seu código deve ficar algo mais ou menos assim:

E ao executar o código, inserindo o valor 10 para a variável A temos:

Aqui nós tivemos duas condições: ele é par ou ímpar, mas e se nós tivéssemos mais de duas condições?

Por exemplo, numa solução de equação de segundo grau que podemos ter até três tipos de solução, como revelado no algoritmo abaixo:

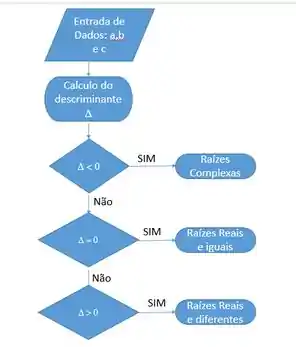
Para isso, podemos usar duas funções: o elseif ou a switch case, então vamos lá.

Função Elseif

A função elseif se traduz do inglês como “mas se”, aplicando para o exemplo da equação de segundo grau e utilizando a seguinte expressão para o ∆ = B 2 - 4 * A * C , podemos escrever um código no Matlab que mostra o tipo de resultado que a equação do 2 º grau possui:

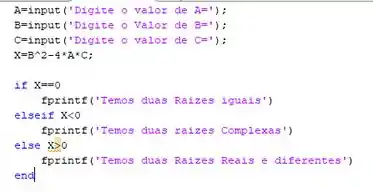
Quando comparamos com o exemplo anterior vimos que entrou um termo a mais que é o e l s e i f . Então se eu tenho vinte testes lógicos eu começo com o i f e após isso faço dezoito casos de e l s e i f e finalizo com o e l s e , pra que somando tudo totalize os 20 testes, belezinha?

Logo, executando o código anterior, temos:

Função Switch Case

A função s w i t c h   c a s e é utilizada para testes lógicos que possuem mais de uma condição, ou seja, utilizamos ela no mesmo caso que o e l s e i f .

Porém ela é pouco utilizada quando comparada com sua irmã, pois o teste lógico precisa trazer um valor ou um conjunto de valores bem definidos.

Para entender melhor vamos ao exemplo abaixo:

O s w i t c h é onde fica armazenada a variável onde associamos cada valor que leva a uma solução diferente, que chamamos de c a s e .

Nesse exemplo o operador vai escrever um número qualquer, o switch vai analisar qual é o valor, ver em qual caso ele se encaixa e após isso realizar alguma tarefa que está dentro desse caso.

Portanto, se eu digito 1 o switch associa o 1 para o case 1 onde imprime o mês de janeiro e se caso digitar 4 , 5 ou 6 ele vai associar isso ao case 4 , 5 ou 6 que imprime o mês de abril a junho, sacas?

Devido a essa rigidez comumente se utiliza a estrutura e l s e i f por ser mais prática.

Bem pessoal, ficaremos por aqui, mas não esquece de ir olhar os exercícios. Selecionamos alguns beeem legais em relação a esse conteúdo.

Então até maisssss.

Funções If e Else

Função Elseif

Função Switch Case

Exercícios Resolvidos

Exercício Resolvido #1

“Elaboração Própria”

  1. Escreva um programa Matlab capaz de:

    1. Ler um raio R de um círculo centrado na origem;
    2. Ler um par de coordenadas (X, Y) de um determinado ponto;
    3. Verificar se o ponto está dentro do círculo.

      4. x 2 + y 2 < R

    4. Imprimir uma mensagem se o ponto se posicionar dentro do círculo. Caso contrário, imprima, também, uma mensagem.

Passo 1

Fala galerinha!

Essa questão já dá pra gente o algoritmo pronto, com passos bem definidos. Nós precisamos receber dados do usuário e então dizer se um ponto de coordenadas x , y está dentro de um círculo de raio R centrado na origem. Por fim, precisamos imprimir uma mensagem informando a resposta ao usuário.

Em diagrama de blocos, esse algoritmo fica assim:

Nessa questão, nossas possíveis respostas são duas: o ponto está dentro do círculo ou não está, ou seja, verdadeiro ou falso. Então, como temos apenas duas condições, iremos utilizar a função if, else.

A função if é uma condição. Se temos uma condição como “se Z

E o else são os casos restantes. Então tudo que não entrar no if, entra no else.

Passo 2

Agora vamos programar!

O primeiro passo é a entrada de dados. Vamos usar a função input para pedir ao usuário os valores das variáveis. Dentro do parênteses à direita do input, escrevemos uma mensagem que o usuário vai receber. O que for digitado pelo usuário, a cada linha, é o valor que será atribuído à variável.

X = i n p u t ( ' e s c r e v a   a q u i   o   v a l o r   d e   X     =   ' ) ;

Y = i n p u t ( ' e s c r e v a   a q u i   o   v a l o r   d o   Y     = ' ) ;

R = i n p u t ( ' e s c r e v a   a q u i   o   v a l o r   d o   r a i o     =   ' ) ;

Agora vamos calcular uma variável Z = x 2 + y 2 que corresponde à distância do ponto à origem.

Z = s q r t ( X ^ 2 + Y ^ 2 ) ;

E então vamos comparar o valor de Z com o raio R e usar o if/else para imprimir a mensagem correta para o usuário. Se Z = x 2 + y 2 < R , então o ponto está dentro do círculo.

i f   Z < = R        

        f p r i n t f ( ' O   p o n t o   ( X , Y )   p e r t e n c e   a   c i r c u n f e r e n c i a ' )

Caso contrário, o ponto não está dentro do círculo:

e l s e          

        f p r i n t f ( ' O   p o n t o   ( X , Y )   n ã o   p e r t e n c e   a   c i r c u n f e r e n c i a ' )

e n d

Passo 3

Uma vez inserido o programa no Matlab seu programa deve ficar algo mais ou menos assim:

Executando o programa para testar, deveremos ter algo do tipo:

Resposta

Uma vez inserido o programa no Matlab seu programa deve ficar algo mais ou menos assim:

Exercício Resolvido #2

“Elaboração Própria”

Escreva codificações Matlab para determinar se uma pessoa é maior ou menor de idade, o programa deve informar se a pessoa é menor de idade ou maior a partir de um número fornecido do teclado, e além disso informar se a idade é válida ou não.

Passo 1

Basicamente a questão pede para criar um programa que a partir de uma entrada de dados de idade gerencie se o cidadão é maior ou menor de idade.

E se caso a idade for inválida no caso de um número negativo, ela informa que a idade não é válida.

Aqui é uma questão básica do processamento de fluxo de sinais com 3 condições, podemos utilizar as funções elseif ou switch, por questão de comodidade iremos utilizar o elseif pois os testes lógicos podem ser inseridos dentro da própria função.

O algoritmo em diagrama de blocos para questão é dado por:

Passo 2

Implementando o algoritmo acima em linguagem de programação temos:

i d a d e = i n p u t ( ' F o r n e ç a   a   i d a d e   d a   p e s s o a   =   ' ) ;

i f   i d a d e < = 0 ;

        f p r i n t f ' I d a d e   e   i n v a l i d a '

e l s e i f   i d a d e   > 0   &   i d a d e   < 18 ;

        f p r i n t f ( ' p e s s o a   é   m e n o r   d e   i d a d e ' )

e l s e   i d a d e   > =   18 ;

        f p r i n t f ( ' p e s s o a   é   m a i o r   d e   i d a d e ' )

e n d

Passo 3

Digitando tudo certinho no Matlab o seu código deve ficar algo mais ou menos assim:

Passo 4

Testando o programa criado temos:

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

“Elaboração Própria”

Uma empresa decide dar um reajuste a seus funcionários de acordo com os critérios seguintes:

  • 50 % para aqueles que ganham menos de 3000;
  • 20 % para aqueles que ganham entre 3000 e 10000 (inclusive)
  • 15 % para os demais

    • Escreva o algoritmo e codificações Matlab capaz de:

    • Ler o salário do funcionário
    • Calcular o valor do reajuste
    • Calcular o salário final
  • Imprimir o resultado

Passo 1

A questão em si pede a elaboração de um algoritmo e uma rotina que ajuste os salários dos funcionários de uma determinada fábrica a partir de uma entrada de dados.

Para a realização precisamos de uma estrutura de fluxo de dados pois para cada valor de salário teremos um ajuste diferente, para a questão temos 3 condições então para resolver precisaremos utilizar elseif ou switch.

Como o teste lógico será aplicado em intervalos de valores é mais prático utilizar a função elseif para respondê-la.

Passo 2

Primeiro passo como a questão pede é a elaboração do algoritmo, então o algoritmo para solução desse problema em diagrama de blocos é:

Passo 3

Uma vez que o algoritmo foi criado basta transformá-lo em uma linguagem de programação, observando que cada caso tem uma saída de dados diferente.

Então o programa vai virar algo do tipo:

X = i n p u t ( ' d i g i t e   a q u i   o   s a l a r i o   d o   f u n c i o n a r i o   = ' ) ;

i f   X < 3000

        y = X * 30 / 100 ;

        z = y + X ;

        f p r i n t f ( ' O   f u n c i o n a r i o   t e v e   u m   a j u s t e   d e   % f   \ n   o b t e n d o   u m   s a l a r i o   f i n a l   d e   % f ' , y , z )

e l s e i f   X > = 3000   & &   X < = 10000

        y = X * 20 / 100 ;

        z = y + X ;

        f p r i n t f ( ' O   f u n c i o n a r i o   t e v e   u m   a j u s t e   d e   % f   \ n   o b t e n d o   u m   s a l a r i o   f i n a l   d e   % f ' , y , z )

e l s e

        y = X * 10 / 100 ;

        z = y + X ;

        f p r i n t f ( ' O   f u n c i o n a r i o   t e v e   u m   a j u s t e   d e   % f   \ n   o b t e n d o   u m   s a l a r i o   f i n a l   d e   % f ' , y , z )

e n d

Passo 4

O programa em Matlab deve ficar algo do tipo:

Ao testar o programa podemos obter informações do tipo:

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

“Elaboração Própria”

Elabore um algoritmo e escreva um programa Matlab para calcular Y para valores de X que estejam no intervalo , a expressão que avalia Y é dada por:

Y = { 3 x 2 + 5 ,     x < 0   - 3 x 2 + 5 ,     x ≥ 0  

Passo 1

Essa questão ela quer calcular os valores de Y, porém para X maiores que zero utilizaremos a função Y = 3 X 2 + 5   e para X menores do que zero se utiliza a função Y = - 3 X 2 + 5 .

Porém, os valores de X válidos apenas estão no intervalo de X ≥ - 9 e X ≤ 9 , então temos o seguinte, temos um teste lógico para verificar se X está no intervalo fechado de - 9,9 se caso o teste dê verdadeiro que que iremos calcular o teste lógico da função.

Se o primeiro teste que corresponde a pertencer intervalo [ - 9,9 ] se caso for falso, o programa deve pedir um novo valor de X.

Passo 2

Primeiro passo como a questão pede é a elaboração do algoritmo, então o algoritmo para solução desse problema em diagrama de blocos é:

Então temos o primeiro teste lógico no qual forma um loop toda vez que inserir um valor de X fora do intervalo do primeiro bloco, uma vez que digita um valor de X válido ele vai para os demais testes para ver qual função que irá ser utilizada.

Passo 3

Transformando o diagrama de blocos em linguagem de programação temos:

X = i n p u t ( ' D i g i t e   o   V a l o r   d e   X       = ' ) ;

i f   X > = - 9   & &   X < = 9

        i f   X > = 0

                F 2 = - 3 * X ^ 2 + 5 ;

                f p r i n t f ( ' O   v a l o r   d e   Y   é   % f ' , F 2 )

        e l s e

                F 1 = 3 * X ^ 2 + 5 ;

                f p r i n t f ( ' O   v a l o r   d e   Y   é   % f ' , F 1 )

        e n d

e l s e

        d i s p ( ' O   v a l o r   d e   X   n ã o   é   v a l i d o   d i g i t e   o u t r o   e n t r e   - 9   e   9 ' )

e n d

Passo 4

Implementado no Matlab seu código deve ficar algo mais ou menos assim:

Testando com valores irá mostrar na sua janela command Windows algo do tipo:

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

“Elaboração Própria”

Dada que uma equação de segundo grau pode ser representada da seguinte forma:

A X 2 + B X + C = 0

Utilizando as equações de Bhaskara, crie um algoritmo e escreva um programa que calcule as raízes REAIS da equação de segundo grau, e se caso a raiz for complexa cancelar o cálculo informando que a raiz é complexa.

Passo 1

A questão pede que a gente crie um algoritmo e um programa que calcule as raízes reais da função de segundo grau.

Se as raízes forem complexas, deve-se parar o cálculo revelando que a raiz é complexa.

Lembrando que para achar as soluções da equação de segundo grau, precisamos de duas equações, uma delas é o discriminante ∆ e outra que é a equação de Bhaskara.

∆ = B 2 - 4 A C

X = - B ± ∆ 2 A

Como temos uma raiz do discriminante, é ele que vai dizer o tipo de solução que nossa equação de segundo grau tem:

  • Se ∆ < 0 , então nossas raízes X não serão reais.

E tudo será definido em função dos coeficientes a , b e c da equação!

Ah essa questão tem diversas formas de programar, cada um faz do jeito que achar melhor meu jeito não é o absoluto. Porém ao testar com os mesmo coeficientes que os meus, você tem que achar o mesmo valor.

Passo 2

Primeiramente, para responder à questão precisamos elaborar o algoritmo!

Para que a equação tenha raízes REAIS, o discriminante precisa ser maior do que 0. Pois se for menor do que 0 a raiz será complexa e o cálculo é parado.

Então começamos calculando esse discriminante e, dependendo do seu valor, calculamos ou não o X1 e o X2.

Sendo assim o algoritmo é algo do tipo:

Passo 3

Uma vez que o algoritmo está pronto, precisamos agora implementar o algoritmo no Matlab.

A entrada de dados fica bem assim:

A = i n p u t ( ' D i g i t e   o   C o e f i c i e n t e   d o   X ^ 2   a q u i       ' ) ;

B = i n p u t ( ' D i g i t e   o   C o e f i c i e n t e   d o   X   a q u i           ' ) ;

C = i n p u t ( ' D i g i t e   o   C o e f i c i e n t e   C   a q u i                 ' ) ;

Agora calculamos o discriminante:  

D e l t a = B ^ 2 - 4 * A * C ;

Então se o discriminante é negativo, já avisamos pro usuário que não há raízes reais:

i f   D e l t a   < 0        

        f p r i n t f ( ' A   e q u a ç ã o   p o s s u i   r a i z e s   c o m p l e x a s   n ã o   p o d e m o s   c a l c u l a r ' )

Caso contrário, ou seja, se o discriminante não é negativo, ele pode ser nulo ou positivo.

Se o discriminante é nulo, nós chamamos a raíz de Y, só pra diferenciar do caso que vai vir depois.

e l s e        

        i f   D e l t a = = 0

                              f p r i n t f ( ' A   e q u a ç ã o   p o s s u i   d u a s   r a i z e s   i g u a i s \ n ' )

                            Y = - B / 2 * A ;

                            f p r i n t f ( ' A   r a i z   d a   e q u a ç ã o   c o r r e s p o n t e   % f ' , Y )

Se o discriminante é positivo, calculamos as duas raízes X1 e X2 e dizemos seus valores ao usuário.

        e l s e   D e l t a > 0 ;              

                f p r i n t f ( ' A   e q u a l ã o   p o s s u i   d u a s   R a i z e s   d i f e r e n t e s \ n ' )

                  X 1 = ( - B + s q r t ( D e l t a ) ) / ( 2 * A ) ;

                X 1 = ( - B - s q r t ( D e l t a ) ) / ( 2 * A ) ;              

                f p r i n t f ( ' A   r a i z   p o s i t i v a   e   n e g a t i v a   d a   e q u a ç ã o   c o r r e s p o n d e   \ n   r e s p e c t i v a m e n t e   a   % f   e   % f ' , X 1 , X 2 )

Precisamos ainda dar o comando end, para fechar os dois if/else que a gente abriu.

        e n d

e n d

Se digitou tudo certinho deve aparecer algo mais ou menos assim para você:

Passo 4

Utilizando A=1,B=2 e C=2 para testar o programa deverá mostrar os valores:

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #6

Adaptada da Questão 3 - Matlab com aplicações em Engenharia – Amos Gilat – página 216

Considere a = 10   e   b = 6 . Verifique as seguintes expressões sem a ajuda do Matlab. Em seguida, use o Matlab e compare com seus resultados.

  1. a > = b
  2. a - b < = b / 2
  3. a - ( b < = b / 2 )

Passo 1

Opa pessoal, o exercício aqui é um exercício onde iremos verificar cada sentença lógica e obter uma resposta.

Após isso vamos colocar as sentenças no Matlab e verificar se nossas respostas estão corretas, beleza?

A proposta do exercício é você brincar com esses testes lógicos e ir pegando a pratica deles.

Passo 2

Substituindo os valores das variáveis a e b temos que a expressão da alternativa a se tornar:

10 > = 6

Como nós sabemos o número 10 é um número que vem depois do número 6, logo o 10 é maior que o 6 o que é verdadeiro.

Ou seja, em linguagem de programação a resposta verdadeira vale 1.

Inserindo no Matlab, temos:

Passo 3

A segunda expressão se torna:

10 - 6 < = 10 / 2

Realizando a operação temos:

4 < = 5

Ou seja, a expressão nos fala que 4 é um número menor do que o 5, o que configura como verdadeiro novamente.

Logo a resposta é igual a 1.

Realizando o teste no Matlab temos:

Passo 4

E a última expressão se torna:

10 - ( 6 < = 6 / 2 )

Realizando as operações temos:

10 - ( 6 < = 3 )

Aqui temos um parêntese em torno do teste lógico, logo somos obrigados a responder ele primeiro.

Sendo assim, o teste lógico nos fala que o número 6 é menor do que o número 3 o que não é verdade, gerando uma resposta falsa que em linguagem de programação vale 0.

Realizando o resto da operação temos:

10 - 0 = 10

Logo a resposta final é 10.

Testando no Matlab temos:

Resposta

  1. Verdadeiro
  2. Verdadeiro
  3. 10

Exercício Resolvido #7

Adaptada da Questão 7 - Matlab com aplicações em Engenharia – Amos Gilat – página 217

Use o MATLAB para gerar uma rotina que a partir de um valor de x digitado pelo teclado ele identifique qual intervalo e calcule o valor da função dada abaixo.

f x = { 4 x + 2     x 2   x + 6.5 1 / 3   - 6 ≤ x ≤ - 2   - 2 ≤ x ≤ - 2.5   - 2.5 ≤ x ≤ 6  

Se o valor de x Não cair no intervalo o programa deve informar qual o erro e pedir para informar o intervalo correto.

Passo 1

Opa galerinha, aqui temos um problema onde temos uma função que assume valores diferentes conforme o x varia.

Esse tipo de função é muito comum na modelagem de sistemas de engenharia, a ideia aqui é utilizar uma estrutura lógica como as i f para poder a partir de um valor qualquer imprimir o valor final da função na tela e indicar a qual intervalo esse valor pertence.

Sendo assim o algoritmo geral desse problema se torna:

1-Entrada de dados – o valor do x

2-teste lógico para ver em qual intervalo se encaixa

2.1-Cálculo do valor da função

2.2-Impressão de tanto da função quanto do intervalo que se encaixou através de uma saída de dados.

Passo 2

Primeiramente vamos precisar implementar a entrada de dados utilizando a função input, cuja a sintaxe corresponde a:

x = i n p u t ' d i g i t e   o   v a l o r   d e   x = '

Agora que inserimos o valor de x precisamos elaborar o código para a realização do teste lógico.

Se o valor de x cair entre o intervalo de - 6 ≤ x ≤ - 2 então vamos calcular a função com a equação 4 x + 2 .

E traduzindo esse intervalo temos que o valor de x precisa ser um número maior do que - 6 para estar dentro desse intervalo e ao mesmo tempo precisa ser menor que -2.

Sendo assim, podemos escrever o intervalo fala na seguinte forma:

x ≥ - 6   E   x ≤ - 2

E para escrevermos no Matlab basta trocar a letra E por & .

Logo o primeiro teste lógico se torna:

Colocamos uma saída que o   f p r i n t f para sabermos identificar em qual intervalo o valor de x digitado está.

Seguindo a mesma ideia para os demais intervalos temos que:

Como temos mais de 2 condições utilizamos o e l s e i f para realização dos demais testes lógicos e se caso não se enquadrar em nenhum teste temos o e l s e para informar que o valor de x não se enquadra em nenhum intervalo.

Digitando tudo certinho o seu código deve ficar algo mais ou menos assim:

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

Adaptada do problema 7 - Matlab com aplicações em Engenharia – Amos Gilat – página 217

O tanque de uma caixa d’água possui a geometria onde a base é um cilindro de diâmetro 25 m e com uma altura de 19 metros e tem uma parte superior de geometria complexa cujo volume e seu raio é dado pelas equações abaixo.

Dentro do tanque há uma boia que indica o nível da água. Sendo assim, escreva uma rotina que determine o volume da água armazenada no tanque, na posição indicada pela boia (altura h).

A rotina deve receber a variável h e retornar o volume em água.

Dados:

R b o i a = 12.5 + 10.5 14 * h - 19

V o l u m e   d a   p a r t e   s u p e r i o r = 1 3 π * h - 19 * ( 12.5 2 + 12.5 * R b o i a + R b o i a 2 )

Passo 1

Opa galerinha, aqui temos um problema onde temos uma função que assume valores diferentes conforme o h varia.

Esse tipo de função é muito comum na modelagem de sistemas de engenharia, a ideia aqui é utilizar uma estrutura lógica como as i f para poder a partir de um valor qualquer imprimir o valor final da função na tela e indicar a qual intervalo esse valor pertence.

O primeiro intervalo é o cilindro e seu volume é dado por:

V = π 4 * D 2 * h = π 4 * 12.5 2 * h

Quando o valor de h ultrapassa a altura do cilindro que é o valor de 19, começamos a entrar na geometria complexa então o volume total é dado por

V = π 4 * 12.5 2 * h + 1 3 π * h - 19 * ( 12.5 2 + 12.5 * R b o i a + R b o i a 2 )

Sendo assim o algoritmo geral desse problema se torna:

1-Entrada de dados – o valor do h

2-teste lógico para ver em qual intervalo se encaixa

2.1-Cálculo do valor da função

2.2-Impressão de tanto da função quanto do intervalo que se encaixou através de uma saída de dados.

Passo 2

Primeiramente vamos precisar implementar a entrada de dados utilizando a função input, cuja a sintaxe corresponde a:

h = i n p u t ' d i g i t e   o   v a l o r   d e   h   m a i o r   d o   q u e   0 = '

Agora que inserimos o valor de x precisamos elaborar o código para a realização do teste lógico.

O primeiro teste lógico equivale em verificar que o valor de h está apenas na altura do cilindro ou seja se h < 19 .

Se caso o a altura não se encaixar nesse primeiro teste lógico só resta ela estar acima do cilindro gerando o segundo teste lógico que é apenas o e l s e .

Que foi gerado através das equações disponibilizadas no problema.

Se você programou tudo certinho no Matlab, temos que seu código deve ter ficado parecido com:

Resposta

Ei, a resposta está no passo a passo :)