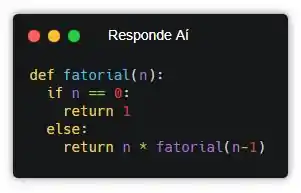
Teoria
Definição de recursão
Fala aí! Aqui na playlist a gente já trocou uma ideia sobre como fazer repetições em Python usando os laços For e While. Mas cada um desses laços tem vantagens e limitações. Por isso eu vim te contar hoje que também dá pra fazer repetições sem usar nenhum laço de repetição, usando uma técnica chamada “recursão”. Essa técnica dá pra gente mais flexibilidade. Bora ver como funciona essa técnica doida!

Cara, primeiramente, calcula pra mim quanto que dá o resultado dessa continha aqui:
![]()
Foi?! Fez a conta?! Eu imagino que o resultado deu 8. Agora, eu vou fazer uma pequena modificação e você calcula de novo, ok?!
![]()
Agora deu 9. Mas, doido… tenho certeza que dessa vez você calculou MUITO mais rápido que na primeira vez. E eu vou te contar o que aconteceu: você já sabia a resposta de parte do processo, então você só somou mais um.

A verdade é que nenhum ser humaninho é capaz de resolver a primeira conta de cara. Eu aposto que quando foi calcular, você fez, malandramente, isso:

Ou seja, no início tu disse que a resposta é 1 + o resto, depois 2 + o resto, até acabar. Isto é, você, sem se dar conta, subdividiu o seu problema várias vezes até chegar em um problema que tu sabe resolver, que é 1+1, porque aí a gente sabe que é 2 só de olhar. Quando eu mudei o problema, aí você fez:
![]()
O nome dessa forma de resolver problemas se chama recursão. A gente usa recursão mentalmente, sem perceber, pra resolver vários problemas da vida real! Mas eu tô te contando isso porque a gente pode usar essa técnica pra resolver problemas de computação também. Tenta lembrar que a ideia da recursão em programação é transformar o mesmo problema em um problema mais simples e resolver ele com a mesma função.

Funções são blocos de código que resolvem um problema específico. Por isso que, na prática, funções recursivas são funções que chamam a si mesmas, jae?! Deixa eu te mostrar um caso onde essa parada é realmente útil.
Aplicação de recursão
Ok! Agora que a gente entendeu o conceito, vamos resolver mais um problema de forma recursiva pra ficar bem claro na sua cabecinha. Eu vou te mostrar um caso clássico, que pode cair na sua prova!

Lembra de fatorial, lá do ensino médio?! O fatorial de n é o produto de todos os números naturais menores ou iguais a n, sem contar com o 0. Um número fatorial é escrito como número inteiro, positivo e seguido de um sinal de exclamação (!). Olha o exemplo de 5 fatorial:
![]()
Agora vamos tentar resolver esse problema. Mano, eu não sei, só de olhar, quanto é 5 * 4 * 3 * 2 * 1. Porém, eu sei que 4 * 3 * 2 * 1 é a mesma coisa que 4 fatorial. Então, a resposta do nosso problema é:
![]()
Pronto. Essa é a resposta. Você talvez se pergunte como que a resposta de um problema pode conter o mesmo problema (nesse caso, o problema era o fatorial e na resposta do problema TEM FATORIAL). E a ideia é justamente essa!

Se a gente não sabe resolver o problema todo, a gente reduz o mesmo problema pra uma ordem menor. 5! É igual a 5 * fatorial do resto do problema. Bom, pra gente resolver esse novo problema, teríamos que, agora, resolver o fatorial de 4.
![]()
Cara***! Caímos no mesmo problema de novo! Não sabia fatorial de 4 e continuo sem saber fatorial de 3.

Mas repara que uma hora o problema vai ser tão simples que a gente vai conseguir resolver.
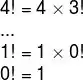
Pra calcular o fatorial de 0 a gente não precisou fazer conta, tá ligado?! Foi um caso muito mais simples. Por isso, a gente usa como condição final. Assim que a gente chega no 0 fatorial, podemos parar de calcular. Agora, a gente volta substituindo os valores que a gente foi encontrando no caminho, afinal, a gente queria o fatorial de 5, lembra?
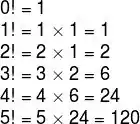
Viu?! Agora a gente pode voltar substituindo… Assim, a gente consegue, com uma mesma metodologia, resolver qualquer problema de fatorial. E a gente pode generalizar:
![]()
Olha que maravilha!

Bora escrever essa técnica doida em Python!
Aplicação de recursão em Python
Vamos escrever uma função que é capaz de resolver qualquer fatorial. Primeiramente, vamos lembrar do manual da recursão:
“Sabe resolver o problema?! Resolva. Não sabe?! Diminua a ordem do problema.”
E como a gente acabou de ver, aplicar essa ideia em problemas fatoriais é tipo assim (com uma linguagem mais pythoniana rsrs):
E olha como a gente poderia escrever em Python:
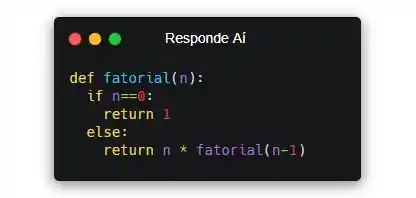
Olha como fica o código da função recursiva que resolve problemas fatoriais… Se n for igual a zero a gente sabe resolver, né?! Então resolvemos. Retornamos 1. Caso contrário, a gente retorna o mesmo problema com uma ordem menor. Guarda bem a cara dessa função, porque a maioria das questões de recursão têm a resposta MUITO parecida com essa, só mudando o que tá nos returns e no if, jae?!

Vamos testar esse programa!
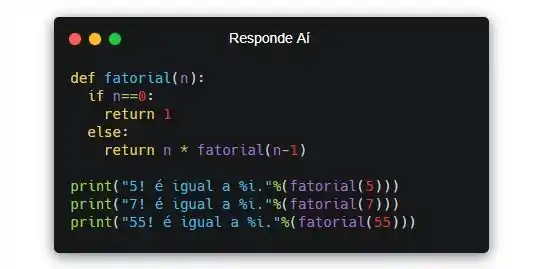
Coloquei uns prints pra gente conferir o resultado. Executando esse programa, a resposta é:

Olha lá! Num passe de mágica a resposta saiu! Uma função relativamente simples, de só 4 linhas, resolveu o problema (e dava pra ser menor!). O mais difícil é pensar recursivamente, e pra ficar craque nisso, é importante fazer um montão de exercícios.
Mas dá uma segurada! Às vezes (muitas vezes) a nossa função dá errado, e vou te adiantar aqui algumas possíveis causas pra você checar caso a sua não funcione, tá?!

Loop infinito (muito tempo)...
Mano, uma função recursiva é a estrutura mais básica de repetição. Seu código entra em loop e só para quando a condição do if é atingida. Se nunca for atingida, o programa vai ficar num loop infinito (letrinhas vermelhas de erro vão te assombrar!).

Vem comigo que vou te mostrar outro exemplo de função recursiva! Imagina que a gente precisa fazer uma função que soma todos os números entre 0 e N, um número inteiro recebido como argumento da função. Vamos supor que o número recebido seja 10. Pô, tu consegue sacar que, assim como no fatorial, esse é um problema que pode ser subdividido em problemas parecidos?!
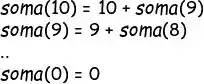
Quando a gente enxerga essa propriedade num problema, aí a gente consegue criar uma solução recursiva! Vamos generalizar...
![]()
Escrevendo essa maravilha em Python, fica assim:
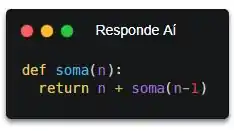
Prontinho! Tá ERRADO! Isso porque, desse jeito, a função vai ficar rodando pra sempre. Do jeito que tá, a função vai chamar a si mesma pra sempre. Por isso que a gente precisa de uma condição que acabe com o loop. Aqui, a gente quer somar todos os números até o zero. Então, quando a gente chegar no zero, é só não chamar a recursão de novo!
Então olha como fica se a gente quiser interromper o somatório no zero:
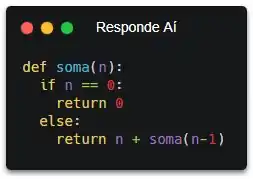
Prontinho! Agora sim, a função vai chamar a si mesma se n for diferente de zero, mas se for igual, vai retornar 0 e acabou. Não vai mais ficar somando pra sempre. Reparou que essa função tá MUITO parecida com a função que calcula fatoriais??? É sempre a mesma cara! E se tu ficar craque em fazer elas, as questões de recursão vão começar a ficar menos complicadas, eu juro!

Por isso eu te espero nos exercícios de fixação! Valeuuuuu!!
Aplicação de recursão
Aplicação de recursão em Python
Loop infinito (muito tempo)...
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
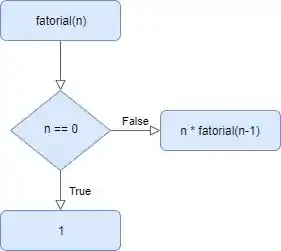
Escreva uma função recursiva que calcule o fatorial de um número recebido como parâmetro.
Passo 1
Fala, meu padrinho! Nessa questão a gente precisa calcular o fatorial de um número usando recursão!

Mas calma, a gente vai tirar essa de letra! Pra começar, nossa função recebe como parâmetro um número inteiro. A nossa função tem essa cara:
Se liga, a ideia da recursão é: sabe resolver? resolve. Não sabe? Diminui a ordem do problema.
Então, qual o caso de fatorial que a gente sabe resolver? Que não precisamos fazer nenhuma conta e nenhum esforço? Bom… É quando n é igual a 0, certo? Que aí podemos dizer de cara que o resultado é 1.

Mas quando não é zero, a gente precisa diminuir a ordem do problema, e pra isso a gente precisa lembrar na moral sobre o que é fatorial.

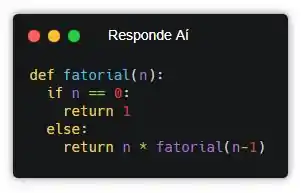
Cara, generalizando, a ideia é que o fatorial de n é a mesma coisa que n * fatorial de n-1.
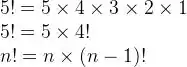
Então, se a gente não sabe o fatorial de um número n de cara, a gente calcula como n * fatorial de n-1.
E pronto! Essa é a resposta! Mas antes, vamos testar..
Passo 2
Pra testar, eu vou colocar um print() embaixo da função, chamando-a com um número inteiro qualquer pra ver se o resultado fica certinho.

E, segundo minha calculadora, o resultado tem que ser 120.
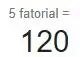
Bora executar o programa pra ver no que dá!
![]()
Olha que maravilha! Funcionou!

Recursão pode ser uma matéria um pouco confusa, mas em geral as soluções são bem pequenininhas, viu?! Cê vai conseguir mandar bem nessa matéria, tenho certeza! Mas bora fazer mais alguns exercícios pra você ficar fera nessa parada. Te espero no próximo!!!
Resposta
Exercício Resolvido #2
PUC-Rio, Lista 7.
Escreva uma função recursiva que receba um número inteiro (n) como parâmetro e retorne o número de vezes que os algarismos 3 e 4 aparecem em n. Exemplo: se n for 239424, a função retornará 3.
Passo 1
Fala, chefe! Aqui a gente precisa contar quantas vezes os números 3 e 4 aparecem em um número inteiro de forma recursiva.

Relaxa! Primeiramente, vamos montar nossa função. Pra contar, a gente só precisa de um dado externo, certo? Que é o número que a gente quer contar os 3 e 4. Então só teremos esse parâmetro, e vamos chamar de n, arbitrariamente.
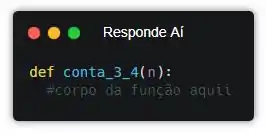
Ok, qual é o caso mais fácil da gente saber se tem 3 ou 4? Bom, se o número for igual a 0 a gente sabe que não tem nenhum 3 e nenhum 4 nele, certo?!

Mas quando não é zero, a gente precisa diminuir a ordem do problema, e pra isso a gente precisa pensar um pouco sobre o que é diminuir a ordem do problema...

Passo 2
Se liga nesse número grandão aqui:
![]()
Mano, tu consegue perceber que a quantidade de 3 e 4 desse número grandão é a mesma coisa que a soma das quantidades de 3 e 4 se a gente dividir ele? Vamos chamar a quantidade de 3 e 4 de q34 pra economizar espaço na ilustração, ok? Olha só:

A gente separou o 5, e eu te digo que a quantidade de 3 e 4 do número de antes é a mesma que a soma da quantidade de 3 e 4 desses dois números que a gente separou agora. Basicamente, se o último dígito for 3 ou 4, a gente diz que a quantidade de 3 e 4 é 1 + quantidade de 3 e 4 sem o último dígito, sacou? Olha o código.
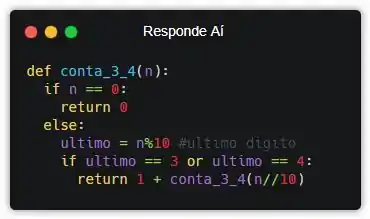
A gente pega o último dígito e checa se ele é 3 ou 4. Se for, a quantidade de 3 e 4 do número inicial é 1 + a quantidade de 3 e 4 que ainda restam, sacou?? Aí o ciclo se repete recursivamente. E caso o último não seja 3 e nem 4, então a quantidade de 3 e 4 é a mesma sem aquele número!
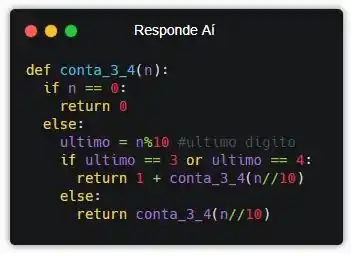
Já que 0 + conta_3_4 é a mesma coisa que não somar nada, a gente não precisa colocar! Mas essa é a resposta, ok? Apesar de ter várias outras respostas possíveis, essa é uma das soluções. O importante é entender a ideia, ok?! Agora, bora testar!
Passo 3
Pra testar, vou chamar a função dentro de um print() embaixo e ver se o resultado bate.
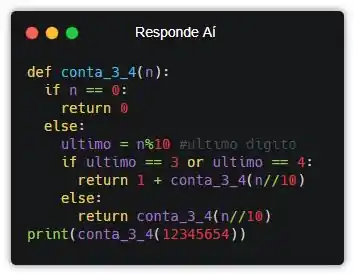
Olha, nesse código a gente espera que o resultado seja 3. Vamos executar!
![]()
E o resultado foi exatamente como esperávamos! MUAHAHHAA! Te espero no próximo, doido!

Resposta
Exercício Resolvido #3
PUC-Rio, Lista 7.
Escreva uma função recursiva que receba um número inteiro positivo como parâmetro e o imprima verticalmente, ou seja, um dígito por linha.
Exemplo:
Se o número recebido for 198 a função irá exibir
1
9
8
Passo 1
Mermão, essa braba! Aqui a gente precisa se ligar em outra propriedade das funções pra gente entender bem o que tá acontecendo.

Mas se liga, vou te falar o segredo da parada. Tu já reparou que, quando uma função termina, a linha execução volta pra onde a gente chamou a função? Assim, olha:
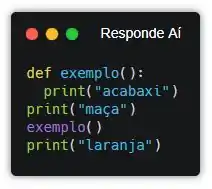
Se a gente executar esse programa, o resultado vai ser esse:

Viu? Esse exemplo foi só pra enfatizar que, quando a função termina, o programa volta pra linha de onde a função foi chamada e continua o fluxo. Isso também acontece se você chamar uma função dentro de outra e, o ponto onde eu quero chegar é, também acontece nas chamadas recursivas! Olha essa função:
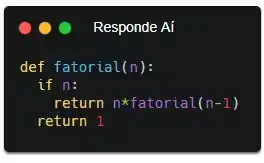
Se parâmetro recebido for diferente de 0, então vai retornar n * fatorial(n-1). Caso contrário (caso seja igual a 0), vai retornar 1. Essa função calcula n fatorial. Mas, vou adicionar uns print() pra te mostrar uma parada dahora!
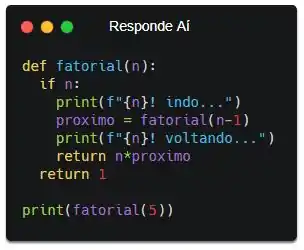
Olha! Eu coloquei alguns prints e chamei a função depois pra calcular 5 fatorial. Olha o resultado desse programa depois de executado:
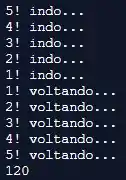
Olha isso! Sacou que as funções recursivas vão empilhando problemas cada vez menores até conseguir solucionar, e depois vai voltando até chegar no problema maior de novo?!

E você já vai sacar o porque eu to te dizendo isso, mas antes, bora voltar pro nosso enunciado e pensar na estrutura que a função do nosso exercício vai ter.
Passo 2
Se liga, se a nossa função vai exibir verticalmente um número, o que a gente precisa pra fazer a função funcionar?? Bom, precisamos do número a ser exibido, certo? Então esse vai ser nosso único parâmetro!
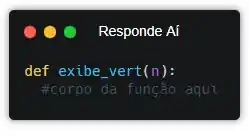
Beleza! Agora, a gente precisa verificar nosso caso base. Bom, o pensamento recursivo é o seguinte: exibe o último e depois exibe verticalmente o resto! Mas, caso o número seja 0, não precisamos fazer nada.
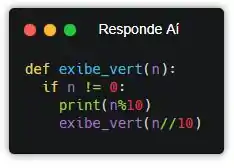
Ou seja, se n for diferente de 0, exibe o último dígito (n%10) e depois exibe verticalmente o resto dos dígitos (n//10).
Obs: caso você não lembre bem, a gente tá separando o último dígito do número. Olha o exemplo:
![]()
Viu?! Com as operações //10 e %10, a gente consegue separar o último dígito de um número inteiro. Beleza! Mas se a gente executar esse código e testar o número 198, não vai ficar igual ao enunciado!
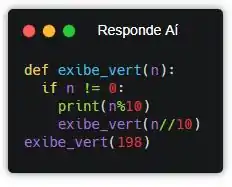
O resultado foi:
![]()
Ala! Ficou ao contrário! Precisamos rever isso!

Passo 3
Calma, relaxou, o que acontece é que a gente tá exibindo o último dígito pra depois exibir o resto verticalmente, mas a gente também pode fazer na ordem contrária (por isso falei sobre a linha de execução no primeiro passo).
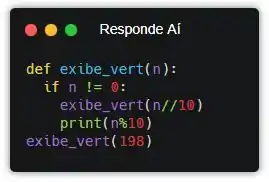
Se a gente fizer a chamada recursiva antes de exibir o último dígito, então todos os dígitos vão ser exibidos na ordem contrária! Lembra que falamos agora pouco que as funções recursivas vão e voltam?! Olha o que acontece quando a gente executa esse programa agora:
![]()
Agora ficou exatamente como no enunciado! A ideia é que dá pra mudar a ordem que as funções recursivas vão executar seus comandos, se é de trás pra frente ou de frente pra trás, só de colocar o comando antes ou depois da chamada recursiva. Nesse caso, colocar o print(n//10) antes da chamada recursiva exibe_vert(n//10) devolve o resultado na ordem contrária de chamar depois, sacou?!

Passo 4
Agora nosso programa já funciona. Mas eu queria te lembrar que “if (n!=0):” é a mesma coisa que “if n:”.
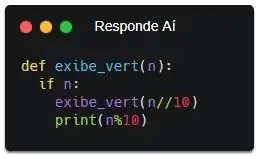
Essa função faz exatamente a mesma coisa que a função que a gente já tinha feito, mas assim fica mais limpa bonitinha!

Essa matéria é bem confusa, né?! Mas calma, continua aqui nos exercícios que a gente vai ficar craque em recursão! Te espero no próximo exercício, hein!
Resposta
Exercício Resolvido #4
PUC-Rio, Lista 7.
Escreva uma função recursiva que seja capaz de intercalar os algarismos de dois números inteiros recebidos como parâmetros. Essa função deve retornar uma string contendo os algarismos intercalados. Quando os algarismos de um número terminarem, os demais algarismos do número que não finalizou devem ocupar as primeiras posições da string resultante.
Exemplo:
n1: 236 n2: 13458
string resultante: '13243568'
Passo 1
Fala aí, doido! Cara, tenho que te contar que essas questões de recursão, depois que você pega o jeito, são bem repetitivas. Então o macete é fazer bastante exercício, jae?! Depois que pega o jeito fica tranquilo! Então vem comigo!

Bora começar falando da estrutura que nossa função vai ter. Os dados externos que nossa função vai receber são n1 e n2, de acordo com o enunciado. Então esses vão ser nossos parâmetros. E o nome a gente mesmo escolhe, e eu vou escolher “intercala”.
Beleza! Vamos dar uma olhadinha no exemplo de resultado que o enunciado deu.
![]()
Até intercalei as cores pra tu reparar que, de trás pra frente, o que tá acontecendo é foi concatenando o último dígito de n1 com o último de n2 até um deles acabar, sacou? Olha…

Assim fica mais fácil de enxergar! Com exceção dos dois primeiros, os outros são o último dígito de n1 com o último dígito de n2. Depois penúltimos, depois ante penúltimos, etc. Bora tentar fazer essa proeza em Python.

Passo 2
Se liga, a primeira coisa que a gente tem que verificar é se os números n1 e n2 são diferentes de 0, né? Levando em consideração que a gente vai cortando o último dígito a cada chamada recursiva, quando um deles acabar, então podemos acabar a recursão. Então vamos começar com o caso base!
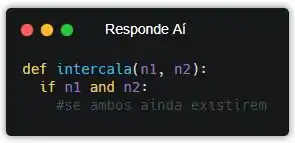
Então, se os dois números, n1 e n2, ainda existirem, a gente vai fazendo aquela parada que a gente observou! Concatenando o último dígito de cada um deles. Pra pegar o último dígito de um número, a gente só precisa calcular o resto da divisão por 10 (%10). E pra concatenar, usamos a função str().
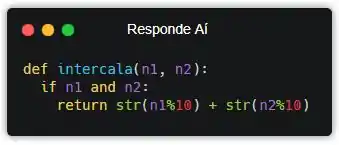
Mas ainda não é só isso nessa linha. Essa função retornaria apenas o 68 do exemplo do enunciado. A ideia é a gente concatenar a chamada recursiva na frente desses dígitos, aí o resultado vai intercalar todos os dígitos, e não só os dois últimos. Se liga:
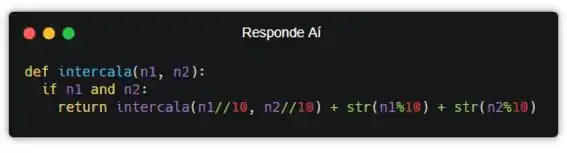
Viu? Olha de novo o exemplo:

Levando em consideração que o primeiro a ser calculado vai ser o 68, depois a gente concatena o 35 na frente usando a função intercala de novo, sem os últimos dígitos (já que tiramos usando o //10), e assim por diante… Agora, só falta a gente lidar com o caso onde um dos dois números acaba.
Passo 3
Mano, quando um dos dois números acaba, a gente só precisa concatenar com o outro todo. Pra fazer isso de forma fácil, vamos usar um truquezinho malandro. Saca só!

Quando um dos números n1 ou n2 acabar, esse número vai ser igual a zero. A gente não precisa saber qual deles acabou primeiro, porque basta a gente somar n1+n2 e o resultado vai ser idêntico ao número restante, já que somar com 0 não vai mudar em nada.
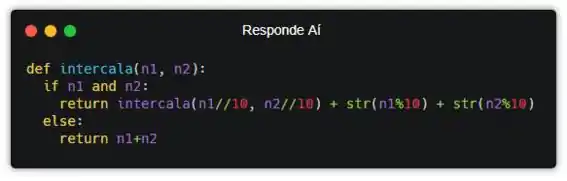
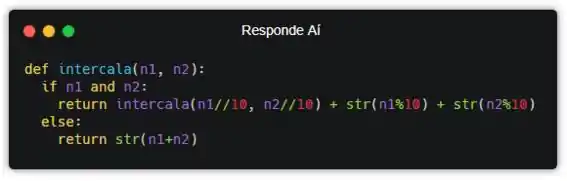
Só que isso ainda não vai funcionar! Isso porque a função tá retornando string no primeiro return, mas no segundo tá retornando um número inteiro. A gente precisa fazer com que todos os casos retornem string. Pra isso, a gente também precisa usar str() no segundo return.
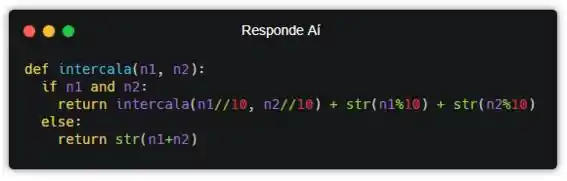
E pronto! Agora a função tá funcionando! Bora testar??
Passo 4
Pra gente testar, bora usar os mesmos dados do enunciado e ver se a resposta sai igual também!
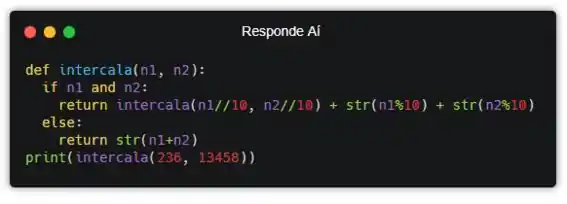
Quando eu executo esse programa, o resultado é esse:
![]()
Exatamente igual ao do enunciado! Ufa! Parece que funcionou hahhaha. Te vejo no próximo, capitão!

Resposta
Exercício Resolvido #5
Universidade Federal do ABC – CMCC, Caderno de Exercícios – Processamento da Informação (edição Python).
Crie uma função recursiva para calcular .
Passo 1
A primeira coisa que nós temos que fazer é definir o escopo da nossa função recursiva, observe que ela deve ser capaz de calcular , logo tanto quanto serão parâmetros da função.
Definindo a função :

Passo 2
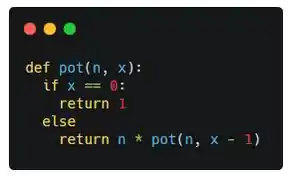
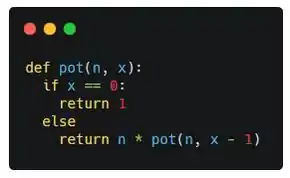
Agora que temos a função definida, temos que identificar o caso básico da nossa recursão, que nada mais é do que a solução de um problema trivial que dará início ao retorno das chamadas recursivas:

Nesse caso, quando nos referimos a uma solução trivial na potenciação temos que , logo quando o valor retornado pela função será 1.
Passo 3
Da mesma forma que identificamos o caso básico, temos que identificar o passo recursivo, que nada mais é do que o padrão de chamadas da própria função que será realizado enquanto :
Esse passo consiste em multiplicar o valor de pela chamada da função com os parâmetros e , observe nesse exemplo como ficarão as chamadas para :
Resposta
Exercício Resolvido #6
Yuri Frota, UFF - Lista 6.
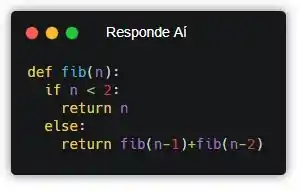
Faça uma função recursiva que receba um número inteiro positivo n e imprima o n-ésimo número da sequência de Fibonacci. Ex: n=5 → 5, n=2 → 1
Passo 1
Coe, truta! Muita coletividade na quebrada! Dinheiro no bolso, sem miséria… É nós!

A primeira coisa que a gente tem que fazer pra resolver essa questão é… saber o que é sequência de Fibonacci. Segundo o Wikipédia, é uma sequência que começa com 0 e 1 e depois vai sendo a soma dos últimos dois números. Tipo assim:
![]()
E assim vai! Parece que a gente tem que criar uma função recursiva que recebe como parâmetro um número inteiro e retorna o número correspondente na sequência… E, pela definição, a gente já saca que a sequência é naturalmente recursiva. Se liga só:
![]()
Vamos começar escrevendo o cabeçalho da função!
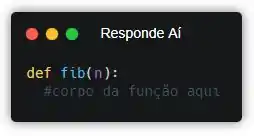
Pronto! Agora, a gente precisa pensar no caso base…
Passo 2
Bora começar vendo o caso que a função termina. Bom, se for 0 ou 1 a gente já sabe a resposta. Olha os números dos itens…
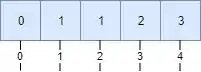
Se liga que o n dá um índice e a gente tem que retornar o número da sequência, heinn! Não confunde! E repara, mano, que os índices e os números da sequência são iguais nos dois primeiros itens. Esses dois itens também são, coincidentemente, nossos casos base. Quando queremos fibonacci de 0, podemos retornar 0. Mesma coisa com o 1, retornamos 1. Vamos escrever em Python!
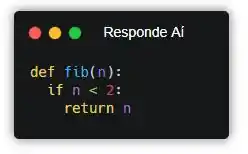
Pronto! Se for menor que 2 (0 ou 1), a gente retorna o próprio valor… Mas se for maior a gente precisa retornar a sequência.
Passo 3
Pra gente retornar o valor da sequência caso seja maior que n, bora dar uma segunda olhada na definição de fibonacci…
![]()
Olha, a gente pode retornar de boas igualzinho na definição da sequência.
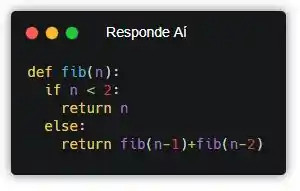
E pronto! Só falta a gente testar!!

Passo 4
Pra testar, eu vou rodar o programa com alguns prints e vou testar com os dados que o professor passou no enunciado pra ver se bate.
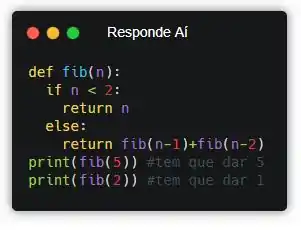
Ala! Depois de executar, deu certinho!
![]()
O resultado foi exatamente como no enunciado! hihihi Finalizamos por hoje, capitão! Te vejo na próxima jornada (chamada exercício de fixação)!

Resposta
Exercício Resolvido #7
Yuri Frota - UFF, Lista 6.
Faça uma função recursiva que receba um inteiro positivo n e imprima a soma dos dígitos de n. Ex: n=215 → 8, n=45 → 9
Passo 1
Fala aí, maninho! Tudo na paz? Se liga, nessa questão o professor quer que a gente some todos os dígitos de um número inteiro usando recursão.

Bora segurar as lágrimas e tentar fazer a questão. Se liga, o que a nossa função precisa saber de dado externo pra funcionar?! Bom… Ela precisa saber qual o número que a gente quer somar os dígitos e só! Então esse vai ser nosso único parâmetro.
E se liga que você pode dar o nome que você quiser pra função e pro parâmetro. Siga seu coraçãozinho! Mas é uma boa ideia dar nomes intuitivos, ok? Usar o nome “n” não é legal, mas eu sou rebelde.

Mentira! Eu escolho nomes pequenos aqui só pra não gastar muito espaço na tela, caso você esteja lendo pelo seu celular… Mas enfim, bora começar a escrever nossa função!
Passo 2
Bom, pra resolver recursivamente a gente precisa fazer o problema grande virar o mesmo problema, só que menor… Como fazer isso nesse caso?! Hmmmmm.

Vamos pensar no número 215, que o professor passou de exemplo no enunciado. Tu percebe que o somatório desse número é um dígito + o somatório do resto?
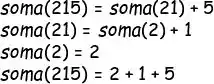
Obs: na teoria, não faz diferença se a gente for separando o último dígito ou o primeiro dígito.
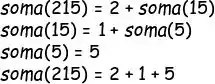
Mas na prática faz, porque a gente não sabe separar, de forma matemática. o primeiro dígito do resto. Mas a gente sabe separar o último, usando divisões por 10. Olha nesse exemplo como a gente pode fazer pra separar o último dígito de um número:
![]()
Show! Mas vamos dar só mais uma olhada em qual vai ser nosso caso base. Percebeu que na ilustração a gente parou de subdividir o problema quando o número só tinha um dígito? Ou seja, quando o número é menor que 10 a gente pode parar. Esse é o nosso caso base. Mas não é a única forma! Dá uma olhada:
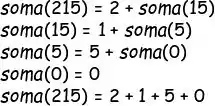
Olha! A gente também consegue fazer n == 0 como um caso base. Problemas de programação sempre têm mais de uma resposta, e eu tô querendo enfatizar que se você fizer diferente não tá errado, ok? Nessa resolução, vou escolher usar o caso base como n

Passo 3
Agora a gente já pensou em qual vai ser o caso base e em como subdividir o problema do enunciado. A gente só precisa escrever essa lógica no corpo da nossa função, em Python.

Pronto! Se for menor que 10 a gente retorna o próprio n, e se for maior a gente retorna a soma do último com o somatório do resto dos dígitos. Vamo só fazer um teste pra ver se a função tá funcionando de boas...
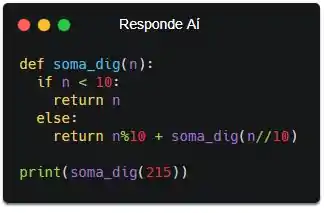
A gente espera que o resultado desse programa seja 8, e quando a gente executa:
![]()
O resultado foi 8 mesmo! EBAAA

Mas antes de finalizar o exercício, vou te falar sobre umas coisas… Se você estiver sem tempo, pode pular pra próxima questão!
Passo 4
Cara, vou copiar e colar aqui a ideia usando n == 0 como caso base.
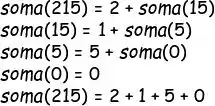
O resultado no fim vai ser exatamente o mesmo, mas pode ser que você prefira fazer dessa forma (eu, geralmente, prefiro). Então eu vou adaptar a última resposta pra usar esse caso base pra você ver como ficaria, ok? Olha:
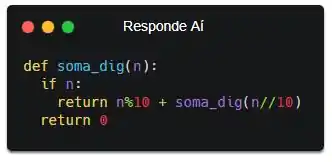
Se liga que o if tá invertido também. O que tá acontecendo é: “se n for diferente de 0, retornar o último dígito + a soma dos outros. Caso contrário, retornar 0”. E é exatamente isso que a gente fez ali em cima nas continhas! Outra coisa que queria falar sobre é que a gente omitiu o else dessa vez. Cadê o else??

Então… Lembra que quando a gente tava falando de funções, eu comentei que a função acaba quando chegamos em um return?! A ideia nesse programa é que se o primeiro if for verdadeiro, a função vai chamar o return e vai chegar ao fim. O segundo return só vai ser executado se o if for falso. Reparou que, nesse caso, o else se tornou desnecessário?!

Se você tivesse colocado também não teria problema, mas eu queria comentar em algum lugar que nem sempre você precisa do else. Quando o primeiro if tem o return dentro, o else se torna desnecessário! Mas isso é só pra complementar seu conhecimento, ok? Na dúvida, coloca o else lá!

Valeuuuuuu!
Resposta

Exercício Resolvido #8
Elaboração Própria
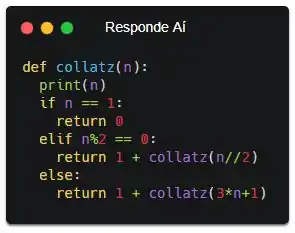
Considere uma função ![]() tal que
tal que
![]()
Escreva uma função, chamada collatz, que recebe um número natural n e retorna o número de vezes que a função f deve ser aplicada, recursivamente, até atingir o número 1. Além disso, a função deve exibir todos os valores de x da sequência. Ex: ao chamar a função com o parâmetro 5, é retornado 5 e exibido
![]()
Passo 1
E aí, maninho! Nessa questão, o enunciado descreve como deve ser nossa função. Até o nome da função foi ditado! Bora obedecer solenemente e criar o cabeçalho da função conforme as ordens do professor...
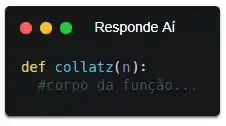
Pronto! Criamos a função e o parâmetro com os mesmos nomes que foram ditos no enunciado. Agora só falta o resto.

Mas, se liga que além disso, o enunciado também deu spoiler de qual vai ser nosso caso base. Nossa recursão tem que parar quando n for igual a 1, certo? Então a gente já sabe que nosso caso base é esse. E também, nossa função tá contando quantas vezes ela mesma foi chamada. Quando n for igual a 1, é pra parar de contar. Então a gente retorna 0!

Pronto! Agora sim, só falta o resto.

Passo 2
Bom, se o número não for igual a 1, a gente precisa aplicar a função f(x) que tá escrita no enunciado. Mas ela depende da paridade do número n! Se n for par temos que fazer uma coisa, e se for ímpar, outra. Pra isso a gente vai ter que usar outro if. Mas, calma, como a gente pode checar se um número é par ou não?

Pô, se um número for par e a gente dividir por 2, não vai sobrar nada. Mas se for ímpar, vai sobrar 1. A gente pode usar isso a nosso favor. Vamos usar o operador de resto de divisão inteira (%)!

É claro que você não precisa, de forma alguma, fazer exatamente igual a mim. Existem várias formas de pensar sobre cada uma das decisões que eu tomo aqui na hora de resolver o exercício, ok?! Show! Agora, no enunciado tá mandando a gente contar quantas vezes vamos chamar a função. Então, bora retornar 1 + a chamada recursiva.
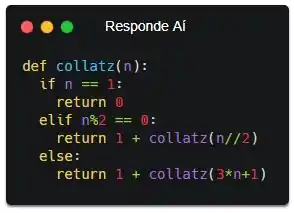
Repara que eu chamo a função recursiva com os parâmetros que foram dados no enunciado. No fim, essa função vai retornar quantas vezes a função foi chamada até n se tornar 1. Vamo testar!
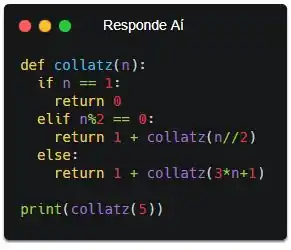
No enunciado diz que, quando chamamos com o parâmetro 5, a função tem que retornar 5. Vamos executar pra conferir.
![]()
Retornou mesmo! Então, até aqui tá funcionando de boas. Mas ainda precisamos fazer a função exibir todos os itens da sequência, igual tá no enunciado.

Passo 3
Cara! A cada elemento da sequência de chamadas de funções é recebido como parâmetro n da função. Então, a gente só precisa, antes de tudo, dar um print() no n.

Se liga só!
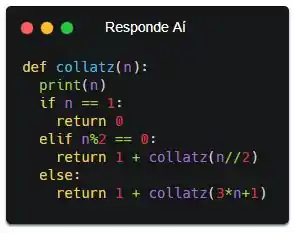
A gente tá exibindo o n antes de qualquer coisa. Agora, se a gente fizer o mesmo teste que a gente fez antes, o resultado vai ser esse:
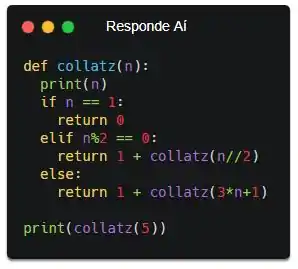
![]()
Parece que tem um 5 a mais no fim, mas tá certo. A função collatz só exibiu até o 1, assim como o enunciado diz. O último 5 foi exibido pelo nosso print() que tá fora da função. A gente usou ele pra testar só!

Por isso, a gente já acabou nossa questão. Finalizamos o exercícioooo!
Resposta