Módulos Math- Python
Produzido por Gustavo BarbosaTeoria
O Módulo Math é muito útil quando queremos fazer cálculos usando o python! Bora ver como ele funciona?!
📢 Clique para ver mais:
Constante pi: math.pi
Vamos começar por uma aplicação simples, você vai fazer uma conta e precisa do número pi. É só colocar 3,14 certo?!
Certo, mas você tammbém pode usar o o código math. pi() Assim:
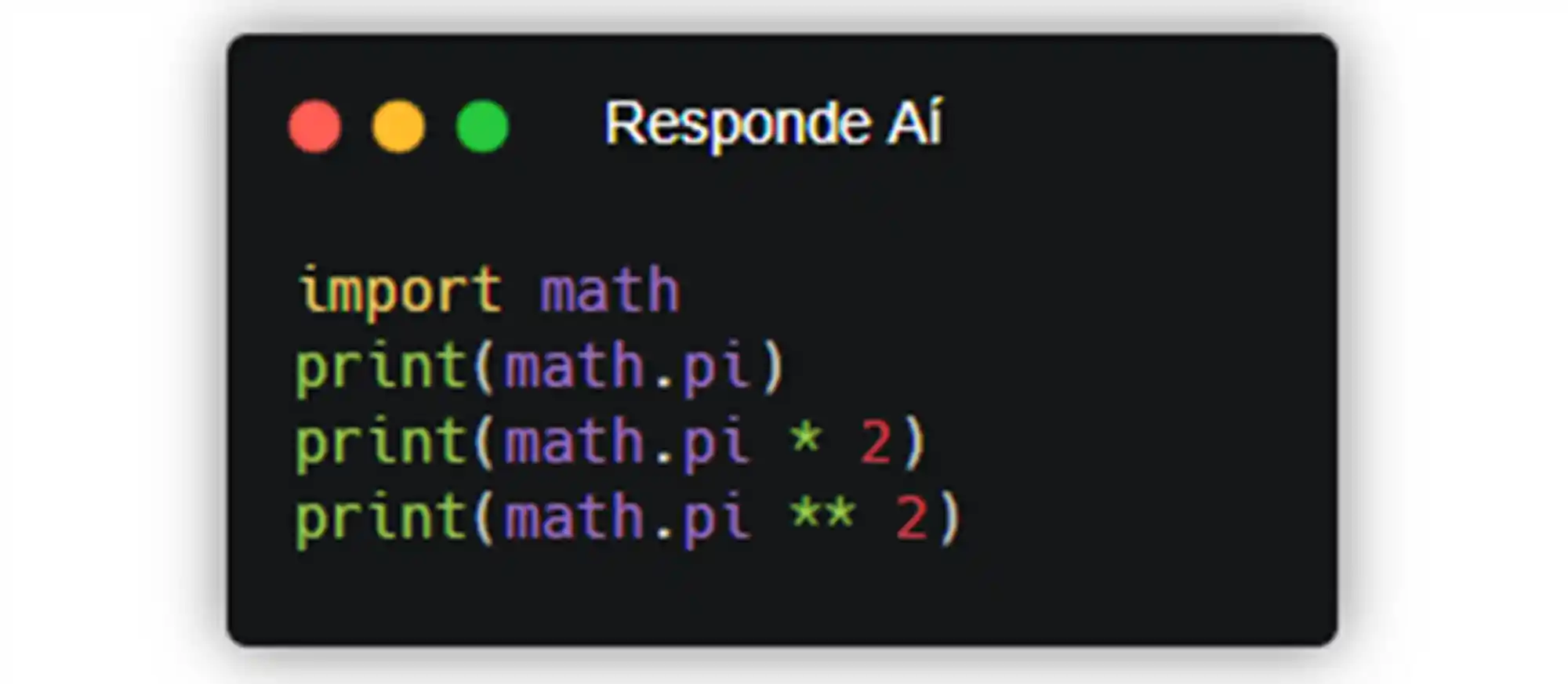
Assim você consegue fazer contas usando o Pi com 15 casas decimais!!
Trigonometria
Para fazer cálculos que envolvem funções trigonométricas você pode usar os códigos math.sin(), math.cos() e math.tan() para calcular o seno, cosseno e tagente respectivamente.
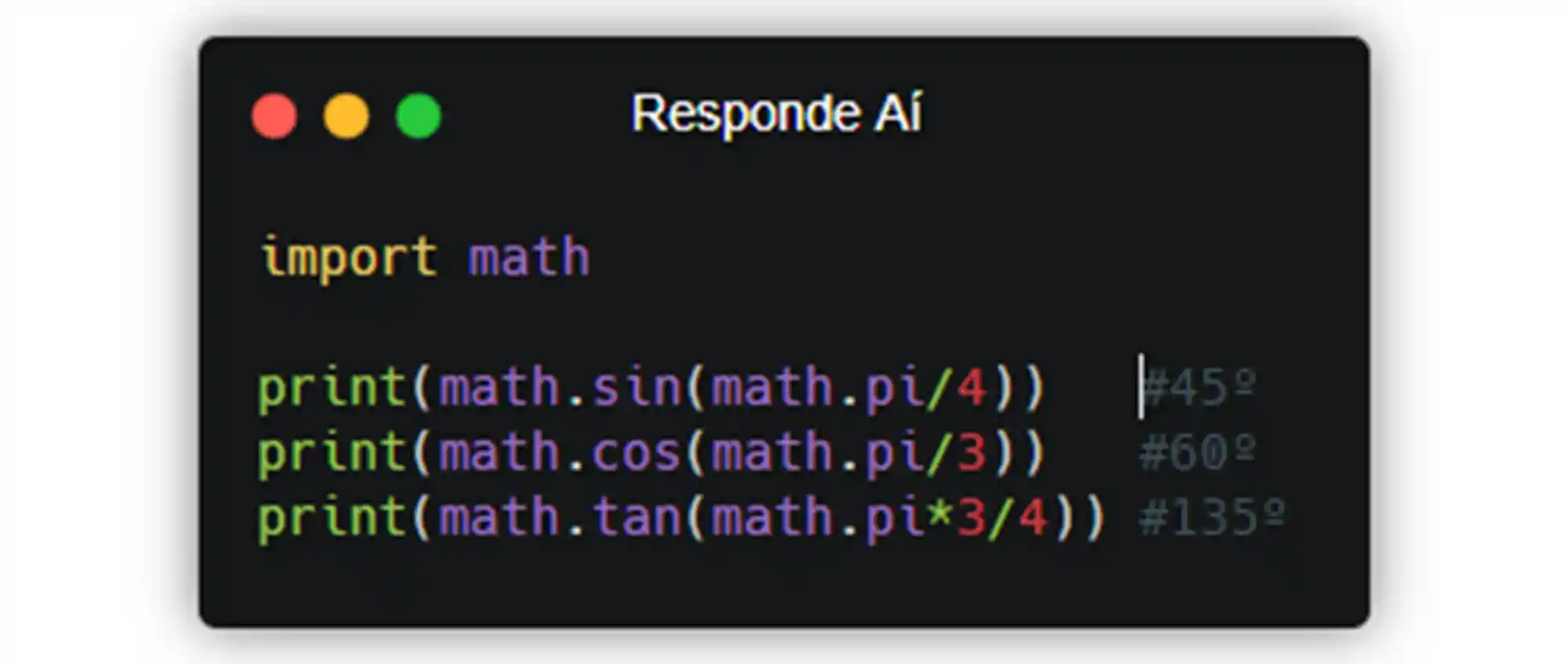
É importante ter em mente que essas funções recebem os ângulos em radianos. Se você quiser converter de grau pra radianos, é necessário usar a função math.radians() para a conversão. Assim:
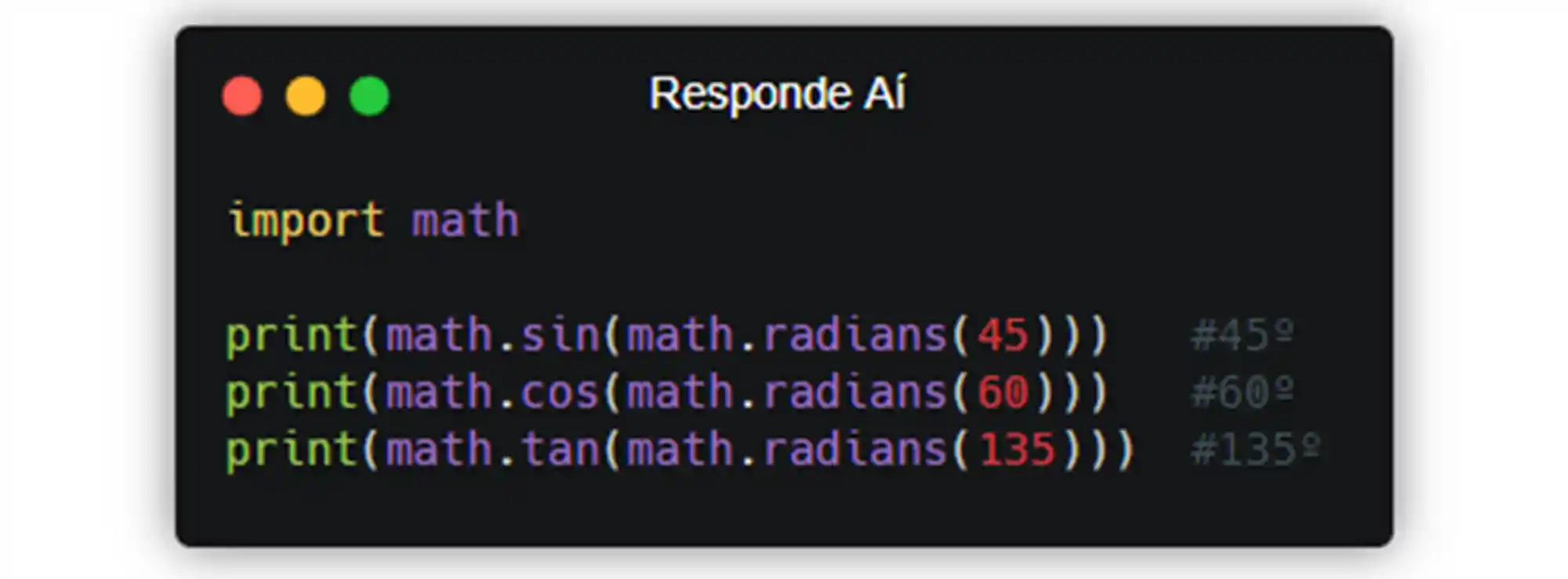
Também é possível o processo contrário, converter radianos pra graus, usando a função math.degrees().
Você também pode conferir esse conteúdo em vídeo:
Raíz quadrada: math.sqrt
Algumas pessoas podem ficar bem confusas calculando raiz quadrada usando expoentes fracionários. O math.sqrt() trás uma solução, se liga nesse exemplo:
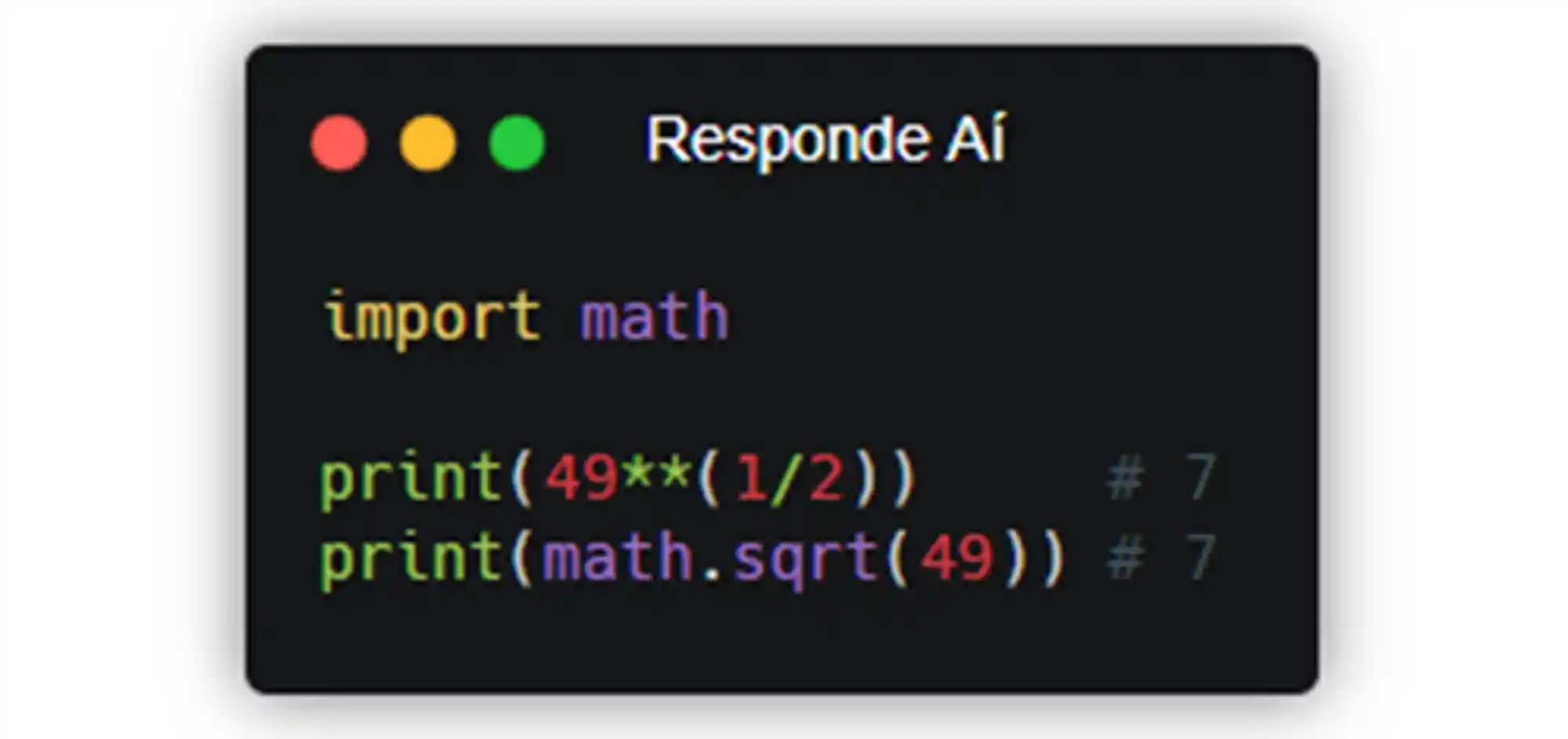
Esses dois códigos fazem exatamente a mesma coisa. Os dois calculam e exibem a raiz quadrada de
Além disso, o expoente fracionário resulta em um número complexo se você tentar calcular raízes negativas. Em contrapartida, o math.sqrt() vai retornar um erro. Se sua questão envolver números complexos, a primeira solução é a única possível.
Na verdade, usar expoente fracionário resolve a maioria dos problemas no calculo de raizes, então minha dica é você sempre optar por ele, ok?!
Logaritmos: math.log
Também pode ser útil utilizar logarítmos pra resolver algum exercício. O módulo math trás um método pra usar logarítmos naturais, para isso usamos o código math.log().
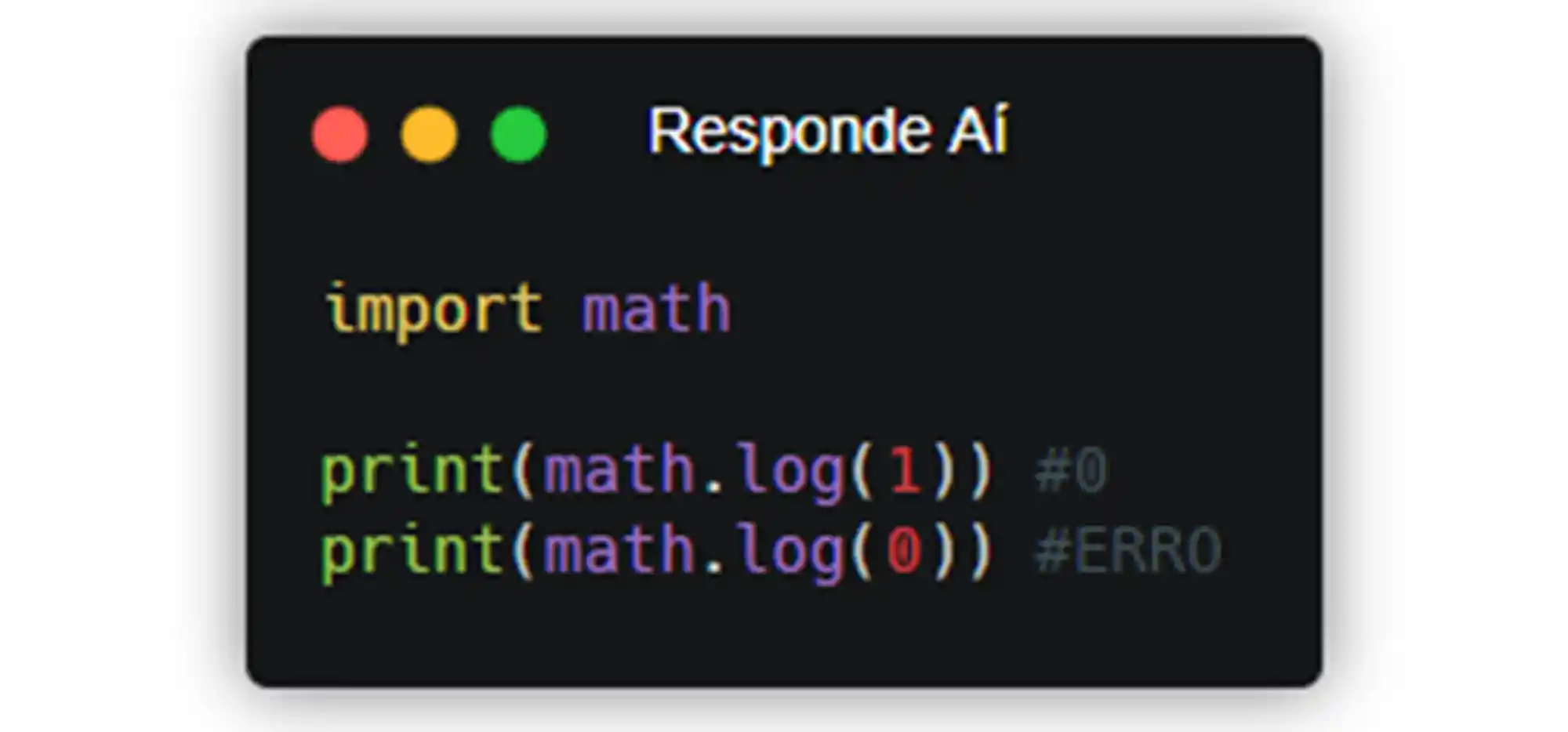
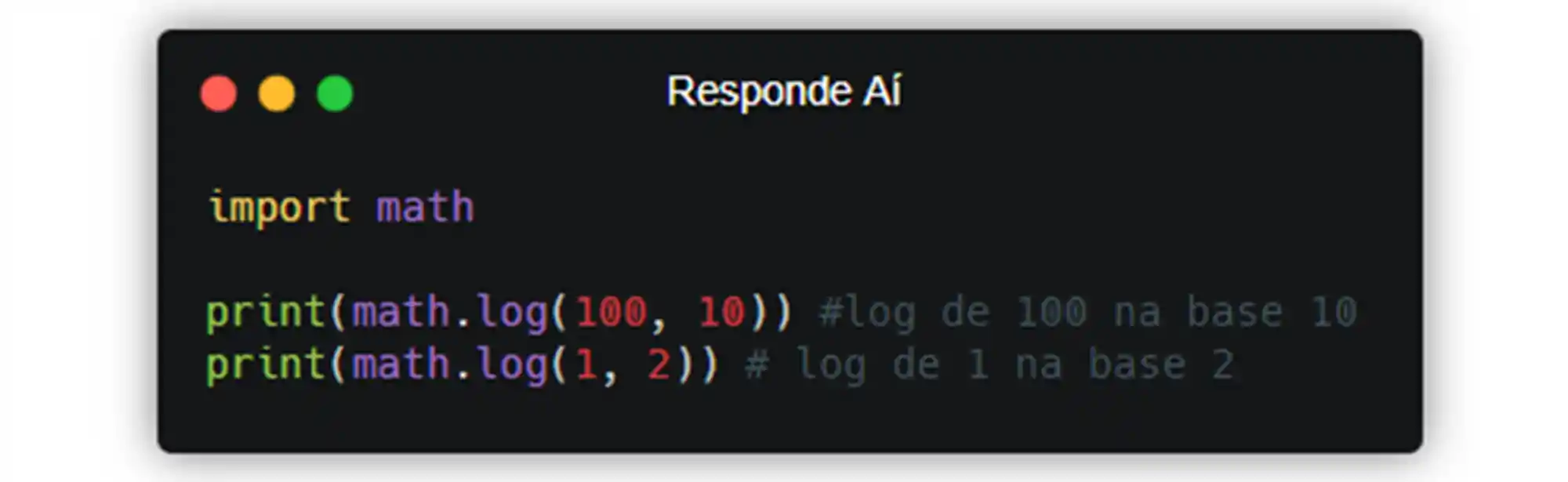
Não esquece que não dá pra calcular log de número negativo, e nem de 0, ok?! O módulo math só abrange números reais (infinitos não são números reais). Caso você queira calcular o log de uma base específica, você pode usar o segundo parâmetro da função math.log() pra escolher a base.
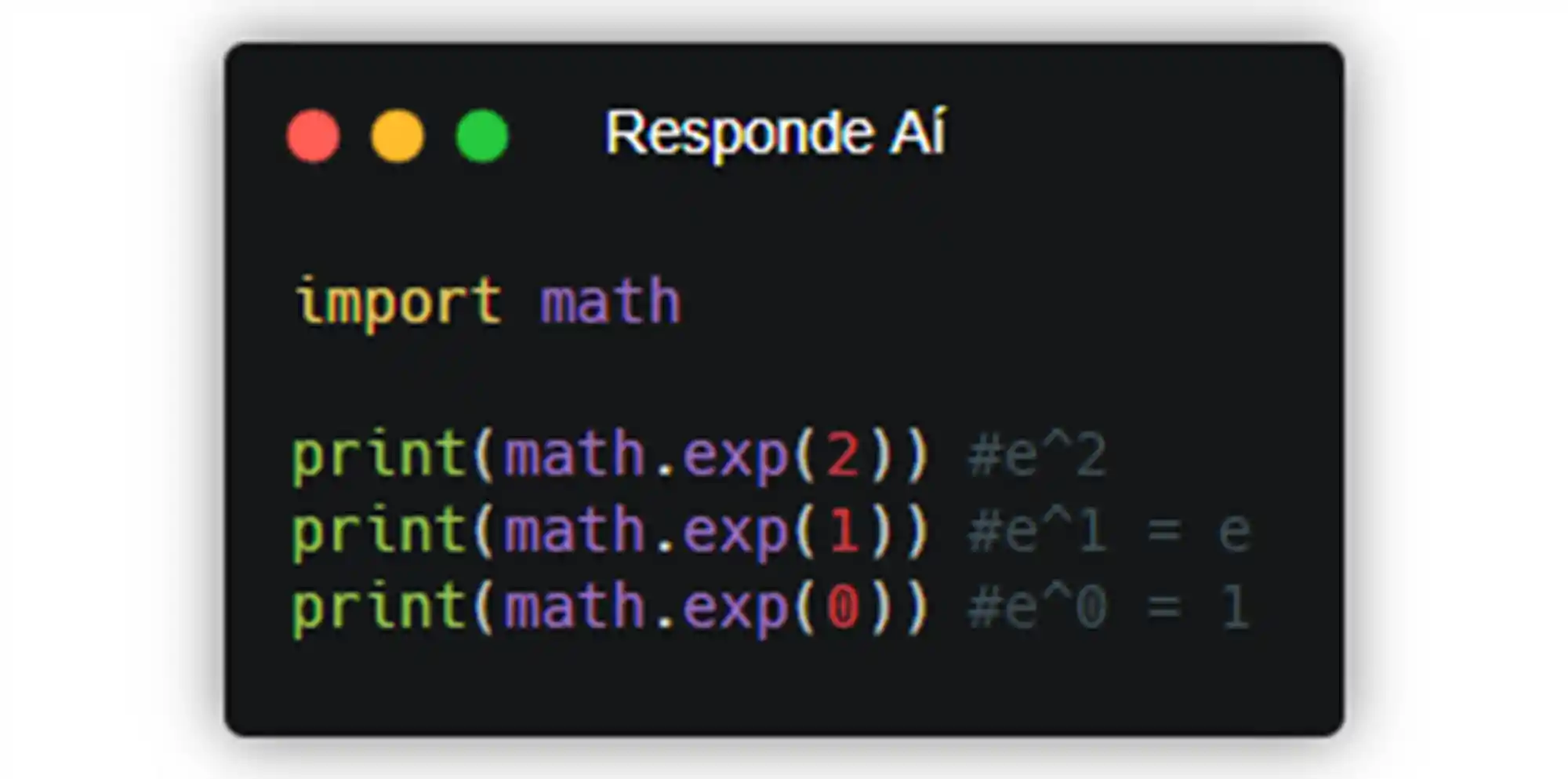
Constante de Euler: math.exp
Assim como pi, o módulo math trás a constante de euler pra gente, mas por meio de uma função. A função math.exp(x) retorna
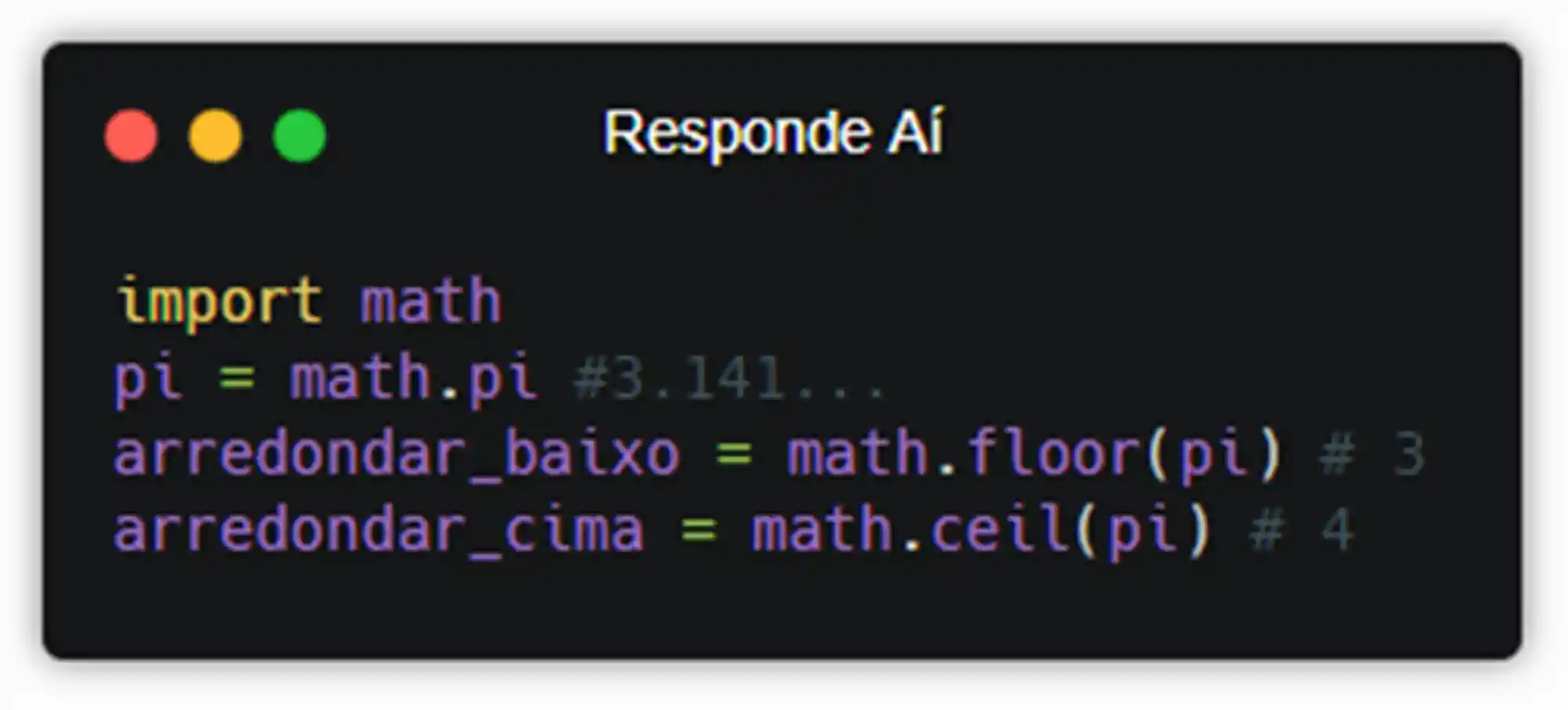
Arredondamentos: math.floor e math.ceil
O módulo math também vem com algumas funções que ajudam a gente quando precisamos arredondar um número real pra um número inteiro. As funções math.floor() e math.ceil() arredondam pra baixo e pra cima, respectivamente. Se liga em como usar:
O módulo funciona da mesma forma, e tem as mesmas funções. Porém, o resultado sempre vai ter parte imaginária. É a única forma de fazer operações com complexos!
Agora bora praticar com exercícios?
Raíz quadrada: math.sqrt
Logaritmos: math.log
Constante de Euler: math.exp
Arredondamentos: math.floor e math.ceil
Exercícios Resolvidos
Exercício Resolvido #1
PUC-Rio, Lista 2.
Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente quantos metros?
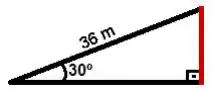
Passo 1
Fala aí, meu parceiro! Parece que voltamos ao ensino fundamental, véi. Mas é bom que a gente relembra essas paradas de trigonometria que cai em todas as matérias de engenharia!

Primeiro, não ficou muito óbvio no enunciado, mas a questão quer saber a altura da barrinha vermelha da figura. Bora chamar essa altura de h pra facilitar nossa vida.
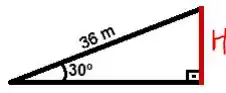
Pra gente descobrir a altura H, bora usar essa regrinha aqui:
![]()
Lembra dela? Seno é igual ao cateto oposto sobre a hipotenusa. Pra nossa sorte, a gente já tem o ângulo theta e a hipotenusa! Vamos substituir os valores.
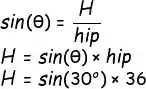
Pronto! Nossa matemática termina por aqui. A partir daqui, vamos fazer essa conta usando Python. Na verdade, essa até dava pra fazer porque o seno de 30º a gente já sabe, mas vai por mim, seu professor de prog vai ficar bolado se a gente não usar Python pra resolver!

Passo 2
Pra resolver aquela continha em Python, primeiro a gente precisa ter acesso ao módulo math, que é onde estão guardadas as funções trigonométricas em Python. Pra isso, vamos importar a biblioteca!
Pronto! Fazer as importações de módulos logo nas primeiras linhas do código é importante pra gente não se enrolar depois, já que as novas funções só estarão disponíveis abaixo dessa linha.

Agora que já temos acesso ao módulo, a gente pode começar a calcular. Vamos, primeiramente, transformar 30º em radianos, jae? Isso porque as funções trigonométricas do módulo math estão todas em radianos. Pra fazer a conversão, bora usar a função math.radians()
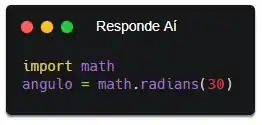
Show! Agora, na variável “angulo” a gente tem salvo o ângulo 30º em radianos. Só falta a gente calcular o valor de H.
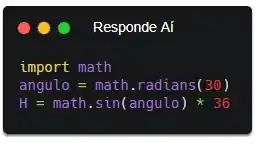
Pronto! Agora a altura foi calculada, mas a gente não sabe qual é ainda. Precisamos que o programa nos informe o resultado.
Passo 3
Pro programa nos contar qual o resultado salvo na variável H, a gente vai usar a função print()! Olha:
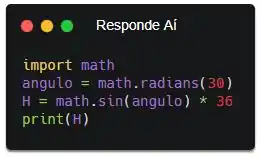
Ala! Agora, ao executar, o programa vai retornar pra gente o resultado. Repara que esse programa não tem valores variáveis. A gente tá usando Python como uma calculadora mesmo. Sempre que executarmos, o resultado será o mesmo. E a ideia do enunciado é essa!
![]()
Ok, esse resultado não tá muito bonito não. Vamos dar uma melhoradinha usando formatação de string. Lembra de formatação de string? São importantes, hein! Dá uma olhadinha no tópico que tem aqui na playlist. Vai ser rápido, prometo.
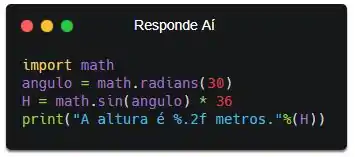
Pronto! Usando formatação e usado uma mensagem mais bonitinha, bora ver como fica o resultado do nosso programa:
![]()
Olha lá, que bonito.

Essa é a resposta do nosso problema. Repara que o enunciado não tá pedindo o programa, mas sim a altura. A resposta é só o número mesmo.

Então é isso! Te vejo no próximo exercício, mano! Valeuuuuu!
Resposta
18 metros.
Exercício Resolvido #2
PUC-Rio, Lista 2.
Um pequeno, porém, horrível, alienígena está no topo da Torre Eiffel (que tem 324 metros de altura) e ameaça destruir a cidade de Paris! Um agente da MIB está no nível do chão, a 54 metros da Torre Eiffel, mirando sua arma a laser no alienígena. Em que ângulo, em graus, o agente deve disparar a arma?
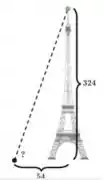
Passo 1
E aí, maninho! Pra resolver essa questão, a gente vai precisar lembrar lá de trigonometria do ensino fundamental. Mas tu reparou que a questão não tá pedindo o código? Só tá pedindo o resultado da conta mesmo… A gente vai escrever o código, executar, pegar a resposta e pronto. A gente até poderia usar a calculadora do PC, mas aí seu professor ia ficar boladão!

Então, bora usar Python pra resolver esse problema. A primeira coisa que a gente tem que se ligar é que, apesar de todo o textinho do enunciado (bem legal, inclusive), a questão só quer saber o ângulo de um triângulo de catetos 54 e 324.
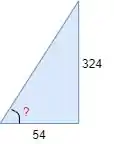
E pra gente descobrir, vamos usar algumas das funções de matemática que são disponibilizadas pra gente no módulo math, que vem junto do python. Mas primeiro, a gente precisa importar o módulo.

Passo 2
Pra importar algum módulo, precisamos usar a palavra-chave “import”, e colocar em seguida o nome do módulo que queremos importar. Olha como fica:
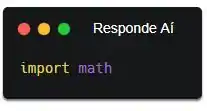
Pronto! Mas não esquece que, caso tenha mais outros códigos no seu programa, é importante que o import esteja nas primeiras linhas. Se não, o professor vai puxar sua orelha, ok?!

Beleza! Agora que já temos acesso às funções matemáticas de Python, bora pensar em como a gente pode descobrir o ângulo do enunciado.

Passo 3
Bom, os dados que nós temos são o cateto oposto e o cateto adjacente ao nosso ângulo. O que esses dados nos lembram?

Isso aí! Nos lembram da tangente!
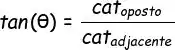
Mas, cara… A gente não quer descobrir a tangente de teta… A gente quer descobrir quanto é o próprio teta! Pra tirar aquela função tan dali, vamos precisar usar a função inversa da tangente. Essa é ruim de lembrar mesmo...

Mas a função inversa da tangente é a função arco-tangente! Então, se a gente aplicar essa função dos dois lados da equação vai ficar assim:
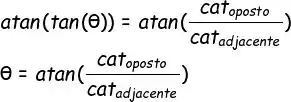
A função arco-tangente cancela a função tangente, e aí sobra só o teta do lado esquerdo da equação! Pronto, já sabemos como descobrir o ângulo… Partiu escrever essa parada em Python!

Passo 4
Bora criar uma variável pra salvar o resultado da nossa conta! Lembrando que as funções inversas trigonométricas em Python são math.asin(), math.acos() e math.atan().
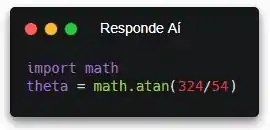
Pronto! Repara que a ordem é importante, ok?! É o cateto oposto dividido pelo adjacente, assim como tá lá na figura! Se colocar ao contrário, o resultado vai ser diferente.

Mas, se liga também que o resultado vai estar em radianos… Bom, não tá errado, mas a gente tá bem mais acostumado a usar graus, e o enunciado também tá pedindo pra converter. Então, bora converter! Pra isso, a gente pode usar a função math.degrees().
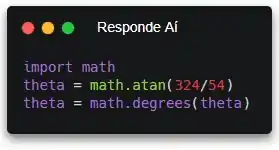
Pronto! A gente atualizou o valor da variável theta, e agora ela tá guardando o ângulo em graus. Show!

O programa tá calculando tudo pra gente, mas ainda precisamos exibir a resposta!
Passo 5
Pra exibir a resposta pro usuário (nesse caso, a gente mesmo), vamos usar a função print() aliada com formatação de string. Se tu não estiver craque em formatar string, dá uma olhadinha nesse tópico, porque bem importante. Tá lá em Operações com String.

Voltando pro nosso programa, vai ficar mais ou menos assim:
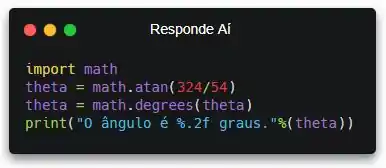
Aí sim! Agora, quando a gente executar, o ângulo vai ser calculado, transformado pra graus e exibido. Vamos executar!
![]()
Pronto! Temos a resposta que nosso enunciado pediu. Agora é só alegria!

Te vejo no próximo exercício, doido! Valeuuuuu
Resposta
O agente deve atirar em um ângulo de 80.54º.
Exercício Resolvido #3
PUC-Rio, Lista 2.
Possuo 4 bolas amarelas, 3 bolas vermelhas, 2 bolas azuis e 1 bola verde. Pretendo colocá-las em um tubo acrílico translúcido e incolor, onde elas ficarão umas sobre as outras na vertical. De quantas maneiras distintas podemos formar essa coluna de bolas?
Passo 1
E aí, maninho! Se liga nesse exercício de combinação que caiu na PUC. Eu MORRIA de medo de análise combinatório no ensino médio.

Agora eu continuo morrendo de medo, mas pelo menos é na faculdade!

A ideia do enunciado é que as bolinhas vão sem empilhadas, e o professor quer que a gente descubra quantas formas diferentes de arrumar essas bolinhas existem. Bom, vamos pensar num problema um pouquinho menor aqui só pra gente pegar a ideia...
Passo 2
Se liga, imagina que a gente tem 4 bolinhas e 4 buraquinhos pra encaixar as bolinhas.

Cara, a ideia é que, no primeiro buraco a gente tem todas as bolinhas na mão ainda… A gente pode colocar qualquer uma das 4, certo? Temos 4 opções. Vamos escolher uma aleatoriamente aqui no nosso exemplo, e vou escrever embaixo quantas opções a gente tinha pra escolher na hora.
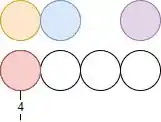
Pronto! Agora, no buraquinho seguinte, a gente pode colocar qualquer uma das outras que sobraram. E sobraram 3! Então a gente tem 3 opções de bolinhas pra colocar no segundo buraquinho ali. Vou escolher a azul agora.
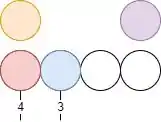
A gente tinha 3 opções na hora de escolher, e escolhemos a azul… Vamos repetir o processo mais duas vezes!
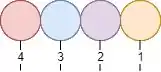
Pronto! A gente organizou as bolinhas de uma forma qualquer, aleatória que eu mesmo escolhi na hora de fazer a ilustração. Mas o importante é pensar em quantas opções a gente tinha na hora de escolher a bolinha. Se a gente multiplicar as opções que a gente tinha em cada etapa, a gente vai ter a quantidade de possíveis combinações! Nesse caso:
![]()
Talvez tu não tenha reconhecido, mas isso é a mesma coisa que 4 fatorial.
![]()
Generalizando: a quantidade de combinações possíveis é a quantidade de bolinhas fatorial. Mas quando temos duas ou mais bolinhas iguais, caímos eu outro problema.
Passo 3
Adicionei mais uma bolinha e coloquei na frente das outras. Se liga em como ficou o nosso mesmo exemplo agora:
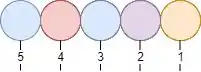
Show! Parece que a gente tem 5 fatorial de possíveis combinações agora. Mas cara, o que acontece se a gente trocar a primeira bolinha com a terceira??

Olha:
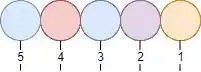
Isso aí mesmo que você tá pensando! Não mudou nada, doido! Como as bolinhas são iguais, não faz diferença se a gente trocar elas de lugar. Então, na verdade, essa combinação é igual a anterior. Por isso, a gente não precisa contar com ela. Pra gente descartar bolinhas iguais, a gente só precisa dividir o total de combinações pela quantidade fatorial de cada bolinha. Nesse caso:
![]()
Show! Sacamos a ideia… Generalizando as combinações com elementos iguais, a gente chega nessa fórmula:
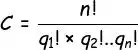
Onde n é a quantidade total de bolinhas e q é a quantidade de cada tipo de bolinha. Partiu escrever essa lógica em Python!

Passo 4
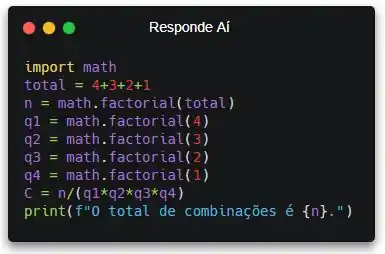
Primeiramente, vamos começar importando o módulo math. Assim, a gente vai ter acesso as funções matemáticas que vêm no Python. Dentre elas, a função math.factorial().
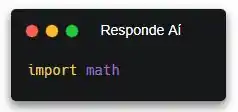
Pronto! Lembra de colocar o import sempre no início do programa, jae?!

Agora, vamos criar uma variável e calcular o total de combinações. Vou chamar a variável de C só pra economizar espaço. Lembrando que o total de bolinhas e a quantidade de cada uma são dados do enunciado...
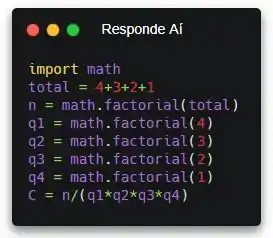
Pronto! Agora a gente só precisa exibir a quantidade de combinações.

Passo 5
Pra exibir a resposta, a gente vai usar a função print(). A danadinha tá em todas.

Mas a gente também vai usar formatação de string, que seria legal você estar sabendo! Caso não saiba do que eu tô falando, dá uma lida rápida no tópico Operações com String. É rapidinho, juro!
Aí sim! Agora, quando a gente executar, o número de combinações vai ser calculado e exibido pra gente.
![]()
E parece que são MUITAS combinações! hahahah

Chegamos ao nosso resultado e finalizamos a questão. Te vejo no próximo exercício, maninho!
Resposta
O total de combinações é 12600.
Exercício Resolvido #4
Elaboração Própria
Elabore um programa que receba três valores reais, A, B e C, e calcule as raízes dessa equação do segundo grau. Para isso, deve usar obrigatoriamente uma função chamada bhaskara, escrita por você, que recebe os coeficientes como parâmetro. Além disso, a função deve calcular e retornar as duas raízes, reais ou complexas, dependendo dos coeficientes. O módulo utilizado deve ser chamado de m e deve existir apenas no escopo da função.
Exemplo 1:

Exemplo 2:
Passo 1
Rapaz, essa parece complicada!

Mas não se preocupe, a ideia dessa questão é abordar umas paradas que só alguns professores cobram. É mais pra complementar o seu conhecimento. Então, se você não tem a menor ideia de como fazer essa questão, é normal. Relaxa!

Primeiro, lembra que a gente fala bastante que é importante colocar o import no início do programa quando a gente quer importar alguma biblioteca/módulo? Isso porque o módulo é importado na linha que a gente digita e só passa a funcionar dessa linha pra baixo. E tem outra coisa: o módulo só vai estar disponível no escopo que você importar!

Ou seja, se tu importar no escopo global (fora de qualquer função), todo o seu programa vai ter acesso. Mas se você usar o import dentro de uma função, o módulo só vai estar disponível dentro do escopo dessa função. Agora tu sacou o que o enunciado tá pedindo, né?!

Passo 2
Vamos começar escrevendo nossa função! O enunciado já disse qual deve ser o nome da função e os parâmetros, então a gente só precisa obedecer.
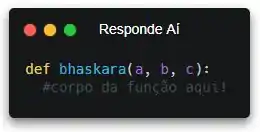
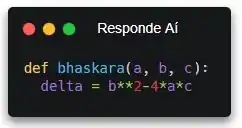
Pronto! Vamos precisar importar algum módulo de matemática pra usar a função de raiz quadrada. Mas devemos escolher se importamos o math ou o cmath, de acordo com nosso delta. Se o delta for menor que zero, a gente importa o módulo de números complexos. Caso contrário, importamos o math.

Vamos começar calculando o delta. Você lembra qual a fórmula do delta??? google pesquisar...
![]()
Beleza! Vamos escrever em Python!
E agora vamos usar o delta pra decidir qual módulo a gente vai importar! Mas mano, tu reparou que quando a gente vai usar as funções de um módulo a gente precisa usar seu nome? Tipo math.pi ou math.cos(). Mas e se a gente não quiser usar o nome do módulo, mas sim outro nome que a gente quiser?!

Aí a gente pode seguir a importação com “import MODULO as NOVO_NOME”. Assim, a gente vai chamar o módulo do nome que a gente quiser! No enunciado, tá mandando a gente importar com o nome de m. Por isso, bora fazer assim:
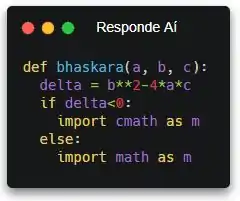
Pronto! Agora, independente do módulo que a gente importar, o nome dele vai estar como “m”.

Passo 3
Se liga que a gente já tem o delta e o módulo de matemática importado. Só precisamos aplicar a fórmula de bhaskara em si e retornar as raízes…

Tá, calma que vou pesquisar a fórmula de bhaskara também.
![]()
Pronto! Bora escrever essa fórmula na nossa função, em Python!
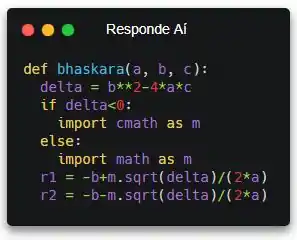
Aí sim! Reparou que a gente usou m.sqrt() independentemente de qual seja o módulo importado? Isso que o professor queria!

Só falta a gente retornar as raízes agora...
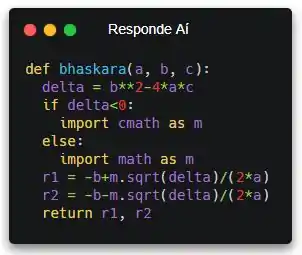
Sim! Dá pra gente retornar várias coisas seguidas por vírgula em uma função! Bora fazer o resto do programa agora…

Passo 4
Com a função pronta, o enunciado também tá mandando a gente perguntar os coeficientes pro usuário, além de nos informar gentilmente que esses coeficientes são números reais. Então, vamos perguntar pro usuário usando a função input() e converter pra número real usando float()!
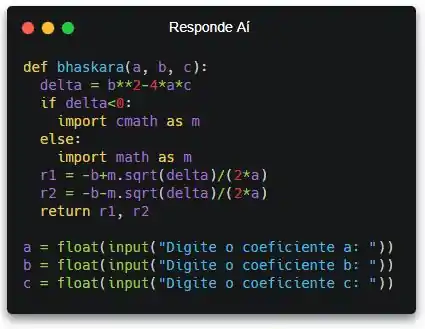
Pronto! Já temos os coeficientes. Pra calcular as raízes, precisamos chamar a função bhaskara passando esses coeficientes como parâmetro. Se liga:
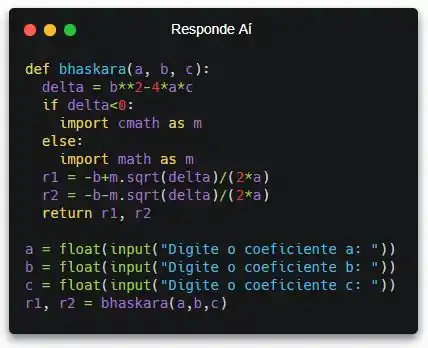
Showsss! Já temos as raízes. Só falta a gente exibir pro usuário!

Passo 5
E pra exibir a resposta pro usuário, usamos o que??? Isso aí, doido! A função print(). Vamos também usar formatação de string pra fazer uma mensagem no mesmo formato dos exemplos do enunciado. Lembra de formatação de string? Tem no módulo de Operações com Strings aqui da playlist, caso você tenha esquecido, jae??

Voltando pro nosso programa, vai ficar mais ou menos assim:
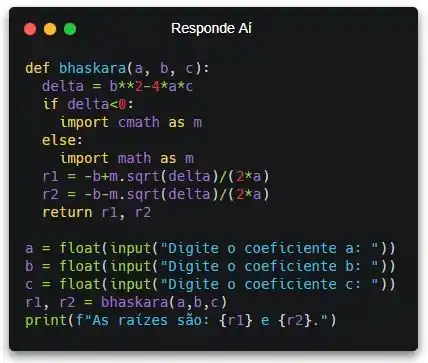
Aí sim! Vou executar o programa e vou digitar as mesmas coisas que o professor digitou no enunciado, e aí a gente confere se tá tudo certinho...

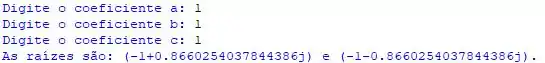
AAAAH MULEKEE!

Te espero no próximo exercício, maninho!! Valeuuuu!
Resposta
Exercício Resolvido #5
PUC-Rio, Lista 2.
O ângulo θ pertence ao 1º quadrante e sen(θ)=17/20. Quanto vale cos(θ)?
Passo 1
Fala aí, carinha! Se liga, nessa questão a gente vai precisar lembrar da fundamental da trigonometria.

O enunciado não dá o ângulo, mas também não pede o ângulo. A gente só precisa saber converter seno em cosseno. E existe uma fórmula que relaciona justamente essas duas funções trigonométricas! Saca só:
![]()
Viu? A gente nem vai precisar saber qual o valor de teta (qual o ângulo).

Mas antes, a gente precisa dar uma mexida nessa fórmula pra gente conseguir colocar nossos dados e pegar o valor que a gente quer. Já que a gente tá querendo descobrir o cosseno, bora isolar!
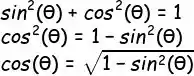
Pronto! Agora, bora substituir os valores que a gente já tem! Nesse caso, a gente só tem o seno de teta.
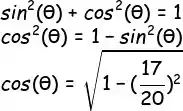
Prontinho! A gente poderia resolver direto na calculadora, mas ai o teu professor vai ficar MUITO PISTOLA!

Pra isso não acontecer, bora fazer usando Python! hahahah
Passo 2
Olha, pra gente ter acesso às funções trigonométricas em Python, vamos precisar importar do módulo math. Pra isso, vamos usar a palavra-chave import. Se liga só:
Aí sim! Agora a gente só precisa fazer a conta. Bora criar uma variável e colocar o resultado da equação que a gente achou dentro dela.
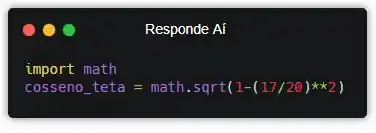
E pronto! Depois dessa linha, a variável “cosseno_teta” vai ter a resposta que a gente quer. Mas a gente precisa exibir esse resultado, se não, nunca vamos descobrir…

Passo 3
Pô, pra gente exibir o resultado a gente pode usar a função print()! Olha:
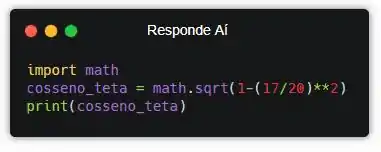
Prontinho! Agora, a gente vai ter a resposta do problema quando executar o programa.
![]()
Resposta feia, né?! Mas é a resposta da questão. Finalizamos essa com sucesso!

Resposta
![]()
Exercício Resolvido #6
PUC-Rio, Lista 2 - Adaptado.
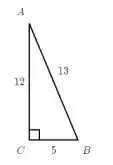
Qual é o valor da raiz quadrada da cossecante do ângulo A? Importe somente as funções necessárias do módulo math.
Passo 1
Fala aí! O bom dessa questão é que só pede cossecante… O ruim é que é ruim de lembrar o que é cossecante!

Mas calma, segundo meu amigo google, cossecante é isso:
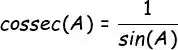
A gente só precisa calcular o seno e dividir 1 pelo seno. Ótimo, mas acontece que a gente tem que fazer isso usando Python, afinal, é uma questão de prog!

E a gente sabe calcular o seno usando Python! Bora por a mão na massa então...
Passo 2
Primeiramente, bora fazer a importação do módulo math, que é onde ficam guardadas as funções de matemática. Mas antes, se liga que no enunciado tá falando pra gente só importar as funções que são necessárias! E COMO QUE A GENTE FAZ ISSO?!

Ok, eu assumo, existe um jeito da gente importar só uma função de algum módulo. E a notação é tipo assim:
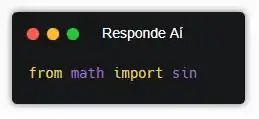
A gente tá falando pra importar a função sin() do módulo math. Isso significa que nosso programa só vai ter acesso a essa função do módulo, e nenhuma outra. Mas e se a gente precisasse importar mais de uma função desse jeito?!

A resposta é que a gente só precisaria separar por vírgulas. Olha, se a gente precisasse da função cosseno também, poderíamos fazer isso:
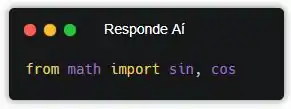
Beleza! E se a gente quisesse importar todas as funções desse jeito??

Nesse caso especial, onde a gente quer importar todas as funções individualmente, a gente usa *. Saca só:
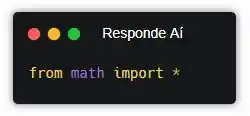
Dessa forma, a gente tá importando todas as funções do módulo… Mas talvez você se pergunte qual a utilidade disso, já que podemos importar o módulo math direto sem usar a palavra-chave “from”, mas bora falar sobre isso daqui a pouco. Antes, vamos voltar pro nosso exercício, que só precisava da função math.sqrt().
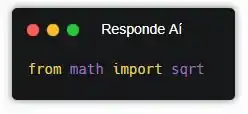
E vamos calcular o que o enunciado tá pedindo.
Passo 3
Aqui, a gente precisa lembrar, lá do ensino fundamental, que o seno é o cateto oposto dividido pela hipotenusa do triângulo retângulo.
![]()
E a gente precisa saber esses dois valores pra conseguir seguir adiante na nossa questão!

Pra descobrir, bora dar uma segunda olhada na figura do enunciado.
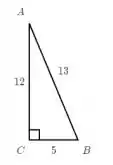
A questão tá pedindo a cossecante de A, e pra calcular a gente precisa do seno de A. Vamos colocar na fórmula o cateto oposto ao ângulo de A então, que nesse caso é 5.
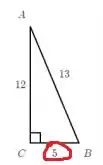
E além dessa dado, também vamos precisar da hipotenusa. A hipotenusa é sempre o maior dos lados, e fica oposto ao ângulo reto (que é representado nas figuras sempre por uma quadradinho). Nesse caso, a hipotenusa é o 13!
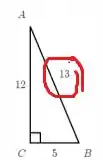
Pronto! Já sabendo os dados, a gente pode colocar na nossa fórmula do seno!
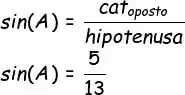
E agora, vamos colocar esse seno na fórmula da cossecante:
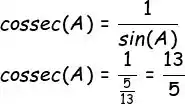
E pra fazer essa proeza, eu resgatei uma propriedade de frações que eu tirei lá do fundo do baú: dividir uma fração por outra é a mesma coisa que multiplicar uma fração pelo inverso da outra. Então, o que eu acabei de fazer foi isso aqui:
![]()
Pronto! Delicinha!

Passo 4
Agora a gente já tem todos os dados e só falta fazer a conta. A gente poderia usar uma calculadora, mas aqui a ideia do professor é treinar as nossas habilidades com o módulo math. Então, vamos resolver em Python.
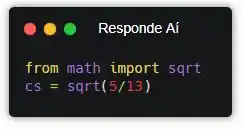
Ala! A gente acabou de criar uma variável chamada cs e colocou dentro dela o resultado da fórmula que a gente tinha acabado de achar no passo anterior. Mas tu reparou que dessa vez a gente não usou math.sqrt() e nem math.cosec()?!

Isso é porque a gente importou as funções individualmente. Quando a gente especifica a função que a gente quer, usando a palavra-chave “from” na importação, a gente não precisa do nome do módulo pra usar. Podemos chamar direto pelo nome sem usar “math.” na frente! É por isso que às vezes é útil importar todas as funções usando *, pra não precisar ficar colocando “math.”.

E agora, a gente só precisa exibir o resultado da conta pra gente responder o enunciado.
Passo 5
Pra gente exibir o resultado, bora usar a função print(). Também vamos usar uma formatação de string pro resultado ficar bonitinho! Se tu não lembra muito bem de formatação de string, é legal tu dar uma olhada no tópico Operações com String aqui da playlist, jae? Seu professor da faculdade vai ficar feliz!

Então, bora escrever nosso print().
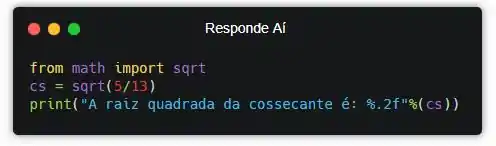
Aí sim! Agora, quando a gente executar, o resultado vai ser calculado e exibido pra gente.
![]()
Pronto! Terminamos a questão.

Te vejo no próximo exercício, hein!
Resposta
A raiz quadrada da cossecante de A é 0.62.
Exercício Resolvido #7
Elaboração Própria
Escreva um programa que receba um número inteiro e exiba quantos dígitos o número tem. Para tal, seu programa deve usar uma abordagem puramente matemática. Seu programa não pode usar conversões de tipos ou laços de repetição.
Exemplo de funcionamento:

Passo 1
Fala aí! Pra saber quantos dígitos tem um número inteiro, a gente poderia simplesmente transformar pra string e verificar seu tamanho com a função len(). Mas, infelizmente o enunciado nos proibiu de fazer isso.

Em vez disso, o enunciado mandou a gente tomar uma abordagem puramente matemática… Mas que tipo de operação matemática a gente pode fazer pra descobrir quantos dígitos tem um número?!

Bom, a gente pode usar logaritmos na base 10. Olha esses testes:
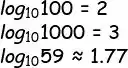
Reparou que se a gente arredondar pra baixo, e depois somar um, o resultado sempre vai ser a quantidade de dígitos?
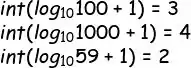
Pegando só a parte inteira dos números e somando 1, resulta na quantidade de dígitos de qualquer número.

Agora que a gente sacou como fazer, bora escrever nosso programa em Python!
Passo 2
Pô, o enunciado tá mandando a gente pedir um número inteiro pro usuário… Pra isso, a gente pode usar a função input() pra perguntar e int() pra converter.
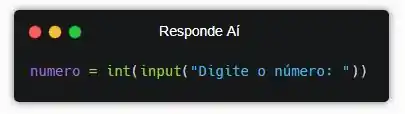
Pronto! Mas tem um problema que a gente tem que pensar… Números inteiros incluem números negativos, mas cara, não dá pra gente calcular log de números negativos!

Mas calma, nossa solução ainda tá de pé! Porque se a gente pegar o valor absoluto do número antes de calcular a quantidade de dígitos, o resultado vai ser a mesma, certo?

Ex: 123 e -123 têm a mesma quantidade de dígitos! Então, antes da gente aplicar a fórmulinha que acabamos de descobrir, primeiro a gente precisa pegar o valor absoluto do número que o usuário digitar! Pra isso, existe a função abs() no Python.
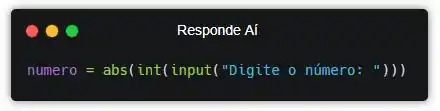
Não esquecendo que as funções são executadas da mais interna até a mais externa, hein… Nesse caso, o passo a passo que Python vai executar ao ler essa linha é esse:
![]()
Show! Agora, a gente já pode calcular direto a quantidade de dígitos.
Passo 3
Pô, pra aplicar a nossa fórmula, vamos precisar da função math.log(). Essa função tá dentro do módulo math, então vamos precisar importar. E é uma boa ideia a gente fazer importações no início do programa, lembra?
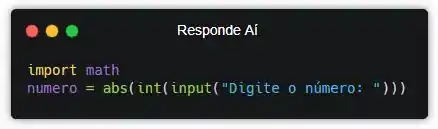
Pronto! Agora, vamos criar uma variável e salvar nela o resultado da nossa fórmula.
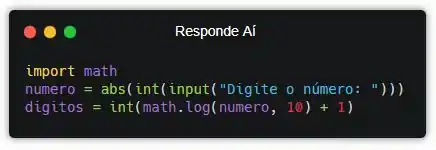
Mas antes da gente continuar, queria comentar com você que transformar pra int() não é a única forma da gente arredondar um número. Além desse jeito, a gente poderia usar as funções math.floor() e math.ceil(). Essas funções arredondam, respectivamente, pra baixo e pra cima. A função também arredonda números reais pra baixo, assim como a math.floor()!

Eu escolhi usar a int(), já que a gente usa ela sempre pra transformar de real pra inteiro, mas você poderia ter escolhido a math.floor(), ok?! Show! Bora continuar…

Cara, a gente já tem o número de dígitos. Só falta a gente exibir!
Passo 4
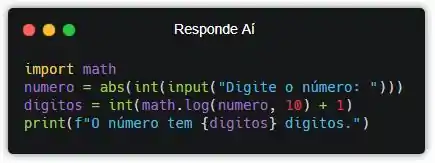
Pra exibir a quantidade de dígitos que o número recebido tem, a gente pode usar a função print().
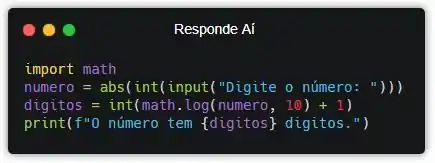
Além da função print(), também coloquei uma formatação de string pra mensagem ficar no mesmo formato dos exemplos do enunciado. Tudo pra puxar saco do professor!

Existem vários tipos de formatação de string, e o ideal é você usar o que o seu professor ensinou na aula, ok? A gente bateu um papo sobre os tipos de formatação no tópico Operações com String aqui da playlist. Dá uma olhada lá, caso tu não se lembre.

Mas ok, agora que terminamos de digitar nossos códigos, vamos testar!
Passo 5
Pra testar, vou executar o código e colocar as mesmas entradas que tem no exemplo do enunciado, pra checar se a saída vai ser igual (apesar de a gente poder conferir só contando os dígitos!).

Executei com os números 100, 1003 e 59. Olha os resultados:
![]()
![]()
![]()
Parece que tá tudo certinho!

Obs: por causa da imprecisão dos computadores, essa abordagem provavelmente vai errar em alguns casos devido ao arredondamento (testa 1000 pra você ver!). Mas seu professor sabe disso, ok? Não precisa se preocupar!

Valeuuuu!
Resposta
Exercício Resolvido #8
PUC-Rio, Lista 2.
Ainda faltam dois sistemas solares para Lúcia visitar em sua viagem, mas sua espaçonave está com pouco combustível. O primeiro sistema, KA-7, está a 1.200 anos-luz (a.l.) de distância, enquanto o segundo sistema, KA-11, está a 1.700 a.l. Sua prioridade é visitar o sistema solar KA-7. Para determinar se ela também poderá visitar o KA-11, é preciso calcular a distância entre KA-7 e KA-11. Se Lúcia vê um ângulo de 52o entre KA-7 e KA-11, qual é a distância entre KA-7 e KA-11?
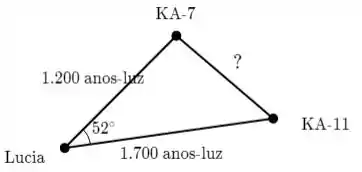
Passo 1
Fala aí, maninho! Apesar de toda estória que veio escrita no enunciado, tudo que a gente precisa fazer é calcular o lado que falta do triângulo da ilustração. Pra isso, a gente vai precisar de trigonometria.

Cara, infelizmente, o enunciado não disse em lugar nenhum que esse triângulo é retângulo, e na ilustração também não tem o quadradinho que indica isso. Isso complica um pouco as coisas.

Mas calma, a gente pode resolver usando a lei dos cossenos! Você lembra dela? GOOGLE:
![]()
É basicamente o teorema de pitágoras aplicado em um triângulo qualquer (sem necessariamente ser triângulo retângulo).

Sendo teta o ângulo entre a e b, e c sendo o lado que a gente desconhece do triângulo, então a nossa equação fica assim:
![]()
Prontinho! Agora a gente só precisa resolver essa conta e vamos ter, de cara, o tamanho do cateto que o enunciado tá pedindo.

Mas, como o exercício é de Prog, vamos esquecer a calculadora e fazer essa conta usando Python, ok?!
Passo 2
Pô, a gente vai ter que usar raiz quadrada e função cosseno pra resolver aquela equação que a gente chegou. E essas funções não vem por padrão, a gente precisa importar elas do módulo math. Pra isso, a gente usa a palavra-chave “import” seguido do módulo que a gente quer importar.
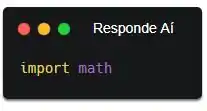
Pronto! Agora temos acesso às funções matemáticas de Python, e já pode fazer as nossas contas usando essas funções!

Mas antes, vamos passar as variáveis do problema pra Python também.
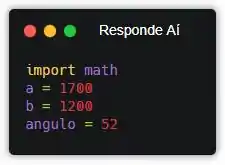
Prontinho! O enunciado deu o ângulo em graus, e a gente escreveu ele ali. Mas lembra que as funções do módulo math sempre consideram que a gente tá usando radianos?! Então, precisamos converter esses 52 graus pra radianos antes de usar...

A gente pode converter direto na hora de criar a variável usando a função math.radians(). Se liga em como fica:
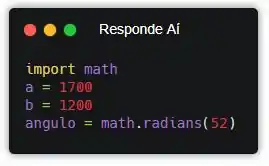
Agora sim! O ângulo tá salvo na variável, mas em radianos. Só falta a gente fazer a conta!
Passo 3
Bora traduzir nossa equação pra Python! Fica mais ou menos assim:
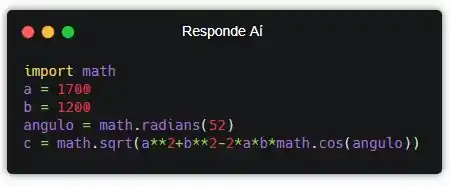
Grande pra caraca! Mas é isso mesmo… Agora, já vamos ter o tamanho do lado que falta no triângulo do enunciado. Mas a gente ainda precisa descobrir qual é!

Então, vamos exibir o resultado da conta usando a função print()!
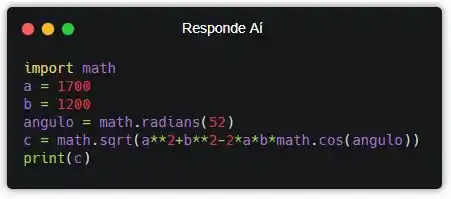
Agora sim! Ao executar esse programa, ele exibirá o tamanho que foi calculado na variável c:
![]()
Ok, essa é a resposta. Mas não tá legal não! Vamos usar formatação de string pra arredondar pra duas casas decimais.
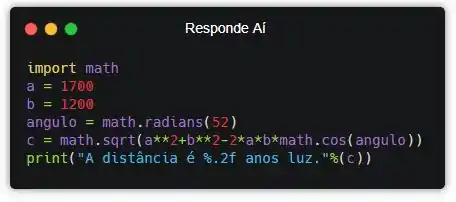
Beleza! Vamos executar de novo e ver como vai ficar o resultado.
![]()
Bem melhor, né?! E essa é a resposta da nossa questão! Finalizamos!

Te vejo no próximo, doido! Valeuuuuu
Resposta
![]()