Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Volumetria de Complexação

Ver Todos os Exercícios

Teoria

Fala aí! Bora conversar sobre Volumetria de Complexação?

A Volumetria de Complexação, também conhecida como titulação de complexação ou titulação complexométrica é uma técnica de análise volumétrica utilizada para a determinação da concentração de íons metálicos em uma amostra a partir da formação de um complexo, formado, geralmente com EDTA.

Confere nesse vídeo abaixo TUDO o que você precisa saber sobre Volumetria de Complexação! 👇

Ou continua comigo no textinho! 😉

Complexos Metálicos

Antes de qualquer coisa, vamos relembrar a teoria ácido-base de Lewis, ela define pra a gente o ácido como uma espécie receptora de pares de elétrons e a base por sua vez tende a ceder pares de elétrons.

A reação de formação de um complexo envolve um ácido e uma base de Lewis, o caso mais simples acontece da seguinte forma:

Onde é um íon metálico que se comporta como um ácido de Lewis e é um ligante que tem a tendência de ceder elétrons, portanto uma base de Lewis!

Complexação com EDTA

O titulante mais utilizado em titulações de complexação é o ácido etilenodiaminotetracético , para os íntimos EDTA  e ele tem essa carinha aqui:

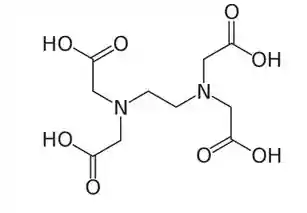
Molécula de EDTA
Molécula de EDTA

Está vendo que ele tem quatro carboxílas?!

Isso quer dizer que o EDTA tem 4 hidrogênios ionizáveis, além disso disso a gente tem dois nitrogênios com pares de elétrons não ligantes, somando tudo o EDTA tem seis grupos doadores de elétrons.

Dessa forma ele é um ligante hexadentado ou seja ele faz seis ligações coordenadas com o metal, com isso ele é capaz de produzir complexos bastante estáveis!

Mas antes de se coordenar com o metal os hidrogênios tem que sair de cena!

O EDTA se ioniza em quatro etapas, em cada etapa ele perde um hidrogênio ionizável, da seguinte forma:

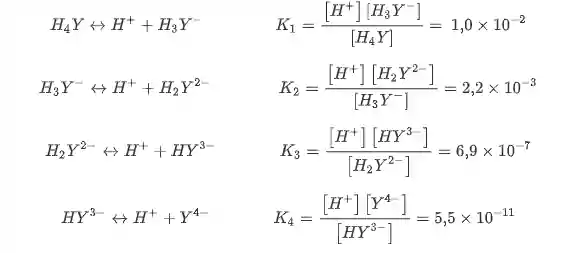
Ionização do EDTA
Ionização do EDTA

Para que a titulação seja o mais eficiente é necessário que o EDTA esteja o mais ionizado possível.

Pelo princípio de Le Chatelier para deslocar o equilíbrio para a direita a gente precisa, ou aumentar a quantidade de reagente, ou diminuir a quantidade do produto. Ou seja, quanto menos presenta na solução mais o EDTA vai se dissociar, logo quando mais alto o maior a concentração de !

Para garantir o da solução titulante, geralmente ela é tamponada no de interesse!

O o diz pra a gente o percentual de presente na solução, podemos ver a sua relação com o na figura abaixo:

ph da solução e a dissociação do EDTA
ph da solução e a dissociação do EDTA

Constante de formação condicional

Temos a seguinte forma geral de uma reação de complexação do EDTA:

Onde é o íon metálico e é sua carga. É interessante observar que como o EDTA faz múltiplas ligações com um único íon, temos uma reação , o que lá na frente facilita bastante nossas continhas!

Agora, vamos supor uma reação de complexação do EDTA com o cátion , temos a seguinte reação química:

Podemos calcular sua constante de formação , que nesse caso é fazendo:

Mas como a gente sabe a concentração de ??!!

Agora é a hora da gente aprender calcular o ele é dado por:

Então ficamos com:

É ai que entra a definição de constante condicional:

Então ficamos com:

Titulação Por Complexação: Curva de Titulação

Em uma titulação estamos interessados em descobrir a concentração do analito usando uma solução titulante de concentração conhecida, o titulante é aqui é o EDTA e o analito é o íon metálico que aqui vai ser o !


Na curva de titulação podemos acompanhar como a concentração do cátion varia a medida que vamos adicionando a solução titulante, vamos construir um gráfico , lembrando que:

Então vamos para o nosso exemplo!

Temos de uma solução contendo a titulado com EDTA em uma solução tamponada a constante igual a .

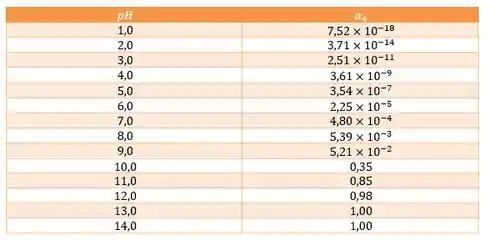
Olhando a tabelinha, achamos , sabendo que , então:

Passo 1: Ponto Inicial

Nesse ponto o volume de EDTA é igual a e , então podemos calcular:

Passo 2: Antes do Ponto de Equivalência

Para acharmos a concentração de cálcio antes do ponto de equivalência a gente tem que subtrair o número de mols inicial do número de mols que complexou , assim:

Adicionando de EDTA:

Calculamos o :

Passo 3: No Ponto de Equivalência

No ponto de equivalência temos:

Substituindo e calculando:

Calculamos o :

Passo 4: Depois do Ponto de Equivalência

Depois do ponto de equivalência temos um excesso de EDTA, para a adição de de EDTA, temos:

Substituindo:

Calculamos o :

Passo 5: Montar a Curva de Titulação

Depois de calcular mais pontos a curva fica com essa carinha aqui:

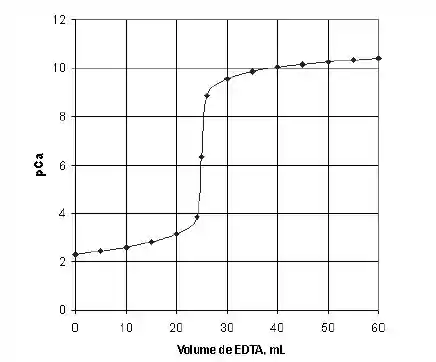
Curva de titulação
Curva de titulação

Agora vamos praticar com exercícios?

Titulação Por Complexação: Curva de Titulação

Exercícios Resolvidos

Exercício Resolvido #1

Lista de exercício de Química Analítica Quantitativa-UTFPR

Uma alíquota de 100,0   m L de água de consumo de uma cidade foi tamponada a p H   10,0   com solução tampão de amônia-cloreto de amônio. Após a adição de indicador calmagite, a solução gastou   21,46   m L de EDTA 5,149 x 10 3   m o l / L. Calcular a dureza de água em mg/L de C a C O 3 .

Passo 1

Temos uma titulação de complexação, entre EDTA e o íon C a 2 + e é por meio da concentração do cálcio que podemos descobrir a concentração de C a C O 3 que o problema esta pedindo pra a gente!

A reação química que esta acontecendo é:

C a 2 + + Y 4 - → C a Y 2 -

Temos a concentração de EDTA, o seu volume gasto para chegar no ponto de equivalência e o volume da alíquota contendo C a 2 + , se estamos no ponto de equivalência, podemos dizer que:

n C a 2 + = n E D T A

Vamos abrir essa expressão, considerando a concentração e o volume original de C a 2 + e do EDTA:

c C a 2 + × V C a 2 + = c E D T A × V E D T A

Isolando a concentração de cálcio:

c C a 2 + = c E D T A V E D T A V C a 2 +

Substituindo e calculando:

c C a 2 + = 5,149 x 10 3 m o l L × 21,46   m L   100,0   m L = 1,1050 × 10 - 3 m o l / L

Ou:

c C a 2 + = 1,1050   m m o l / L

Passo 2

Agora temos a concentração de C a 2 + em m m o l / L e queremos chegar na concentração de C a C o 3 em m g / L , sabendo que:

c C a C O 3 = c C a 2 +

Podemos calcular então:

c C a C O 3 = M M C a C O 3 × c C a 2 +

Precisamos da massa molar do analíto:

M M C a C O 3 = 100,0869   g / m o l

Por conveniência podemos escrever assim:

M M C a C O 3 = 100,0869   m g / m m o l

Substituindo:

c C a C O 3 = 100,0869 m g m m o l × 1,1050 m m o l L

Agora é só calcular:

c C a C O 3 = 110,6   m g L

Prontinhoo!!!

Resposta

c C a C O 3 = 110,6   m g L

Exercício Resolvido #2

Lista de Química analítica I-UFF professor Wagner Pacheco.

As constantes dde dissociação ácida do EDTA são K 1 = 1,02 × 10 - 2 , K 2 = 2,14 × 10 - 3 , K 3 = 6,92 × 10 - 7 e K 4 = 5,50 × 10 - 11 . Usando esses dados, encontre α (para a forma Y 4 - ) em pH 5 .

Passo 1

A gente quer achar o α para formar Y 4 - , ou seja o α 4 , sua fórmula é essa aqui:

α 4 = K 1 K 2 K 3 K 4 H + 4 + K 1 H + 3 + K 1 K 2 H + 2 + K 1 K 2 K 3 H + 1 + K 1 K 2 K 3 K 4

O problema da pra a gente os valores dos K s e diz que o p H = 5 !

Bem, se o p H = 5 então H 3 O + = 10 - 5 , agora temos muitas contas pela frente, então vamos primeiro calcular cada parcelinha dessa expressão pra depois juntarmos tudo?!

Passo 2

Começando com o numerador:

K 1 K 2 K 3 K 4 = 1,02 × 10 - 2 × 2,14 × 10 - 3 × 6,92 × 10 - 7 × 5,50 × 10 - 11 = 8,31 × 10 - 23

Agora vamos para o denominador:

H 3 O + 4 = 10 - 5 4 = 10 - 20

K 1 K 2 K 3 H 3 O + = 1,02 × 10 - 2 × 2,14 × 10 - 3 × 6,92 × 10 - 7 × 10 - 5 = 1,51 × 10 - 16

K 1 K 2 H 3 O + 2 = 1,02 × 10 - 2 × 2,14 × 10 - 3 × ( 10 - 5 ) 2 = 2,18 × 10 - 15

K 1 H 3 O + 3 = 1,02 × 10 - 2 × ( 10 - 5 ) 3 = 1,02 × 10 - 17

α 4 = 8,31 × 10 - 23 10 - 20 + 1,51 × 10 - 16 + 2,18 × 10 - 15 + 1,02 × 10 - 17 + 8,31 × 10 - 23

Colocando tudo na calculadora, achamos:

α 4 = 3,55 × 10 - 7

Que é um valor bem pequeno e reafirma o que a gente conversou lá na teoria! Quanto mais básica a solução, mais o EDTA vai se dissociar!

Resposta

α 4 = 3,55 × 10 - 7

Exercício Resolvido #3

Lista de Química analítica I-UFF professor Wagner Pacheco

Uma solução foi obtida pela mistura de 50   m L de uma solução 0,020   m o l de EDTA com 50   m l de uma solução contendo 2,0 × 10 - 3   m o l   L - 1 de F e 3 + e 2,0 × 10 - 3   m o l   L - 1 de C u 2 + . Considere o p H da solução final igual a 2,00 . Calcule as constantes condicionais e as concentrações de F e 3 + e C u 2 + no equilíbrio. Dados: K C u Y 2 -       = 5,30 × 10 18 , K F e Y -   = 1,30 × 10 25 , α p H = 2 = 3,71 × 10 - 14 .

Passo 1

Temos as seguintes reações químicas acontecendo:

C u 2 + + Y 4 - → C u Y 2 -

F e 3 + + Y 4 - → F e Y -

O problema pede pra a gente as constantes condicionais K ' C u Y 2 -   e K ' F e Y -   e as concentrações de F e 3 + e C u 2 + no equilíbrio, vamos começar com as constantes condicionais!

Primeiro K ' C u Y 2 -   , que pode ser calculada por:

K ' C u Y 2 -   = K C u Y 2 -   ×   α 4  

Substituindo:

K ' C u Y 2 -   = 5,30 × 10 18 × 3,71 × 10 - 14 = 1,97 × 10 5

Agora K ' F e Y -   :

K ' F e Y -   = K F e Y -   ×   α 4

Substituindo e calculando:  

K ' F e Y -   = 1,30 × 10 25 ×   3,71 × 10 - 14 = 4,82 × 10 11

Passo 2

Agora que a gente tem as constantes condicionais, podemos calcular a concentração dos íons no equilíbrio, começando pelo íon de cobre:

K ' C u Y 2 -   = [ C u Y 2 - ] C u 2 + c T

c T é a concentração total do EDTA, que o enunciado não da direitamente ele da o volume e o número de mols, logo:

c T = 0 , 020   m o l × 50 × 10 - 3 L = 1 × 10 - 3 m o l   L - 1

A concentração do complexo é dada pela concentração inicial de C u 2 + menos o cobre dissociado do complexo, maaas como a constante de formação é muito grande, podemos considerar:

C u Y 2 - = c C u 2 + - [ C u 2 + ] ≈ c C u 2 +

Isolando a concentração de cobre:

C u 2 + = c C u 2 + K ' C u Y 2 -   c T

Agora podemos calcular:

C u 2 + = 2,0 × 10 - 3 1,97 × 10 5 × 10 - 3 = 1,01 × 10 - 5 m o l / L

Passo 3

Seguindo o mesmo raciocínio, podemos calcular a concentração de F e 3 + :

[ F e 3 + ] = c F e 3 + K ' F e 3 +   c T

Substituindo e calculando:

F e 3 + = 2,0 × 10 - 3 4,82 × 10 11 × 10 - 3 = 4,1 × 10 - 11 m o l / L

Aweee, prontinho!!

Resposta

K ' C u Y 2 -   = 1,97 × 10 5

K ' F e Y -   = 4,82 × 10 11

C u 2 + = 1,01 × 10 - 5 m o l / L

F e 3 + = 4,1 × 10 - 11 m o l / L

Exercício Resolvido #4

Questão de prova- Química Analítica II UFF Professor Itabirano.

(Adaptada) O íon M 2 + ( 100,0   m L de uma solução 0,0500   m o l   L - 1 do íon metálico tamponado a p H = 9,00 ) foi titulado usando uma solução de EDTA 0,0500   m o l   L - 1 .

  1. Qual o volume equivalente ( V e q ) em m L ?
  2. Calcule a concentração de M 2 +   quando V = 1 2 V e q ;
  3. A constante de formação K f = 10 12 , calcule a constante de formação condicional K f ' para α 4 = 0,041 .

Passo 1

Vamos nessa, o volume equivalente é o volume de EDTA no ponto de equivalência, nesse caso:

n E D T A = n M 2 +

Mas o número de mols é dado pela concentração multiplicada pelo volume, e é o volume que a gente quer!

c E D T A × V E D T A = c M 2 + × V M 2 +

Isolando V E D T A :

V E D T A = V M 2 + c M 2 + c E D T A

Agora a gente pode substituir:

V E D T A = 100,0   m L 0,0500   m o l   L - 1 0,0500   m o l   L - 1 = 100,0   m L

Awee, uma já foi!!

Passo 2

Agora a gente quer conhecer a concentração do metal na metade do ponto de equivalência, nesse caso V E D T A = 50,00   m L .

A gente tem que subtrair o número de mols inicial do número de mols que complexou , e dividir pelo volume total, assim achamos a nova concentração:

M 2 + = M 2 + i n i c i a l × V M 2 + -   E D T A × V E D T A V M 2 + + V E D T A

Substituindo:

M 2 + = 0,0500   m o l   L - 1 × 100,0   m L -   0,0500   m o l   L - 1 × 50,0   m L 100,0 + 50,0

Calculando, achamos:

M 2 + = 0,0167   m o l   L - 1

Passo 3

Pra acabar o problema pede pra a gente calcular a constante condicional, que é dada por:

K f ' = K f × α 4

Substituindo e calculando:

K f ' = 10 12 × 0,041 = 4,1 × 10 10

Shooow!!

Resposta

  1. V E D T A = 100,0   m L
  2. M 2 + = 0,0167   m o l   L - 1
  3. K f ' = 4,1 × 10 10

Exercício Resolvido #5

SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 17 , exercício 17-32.

(Adaptado) Considere a titulação de 50,00   m L d e S r 2 +   0,01000   m o l   L - 1 com EDTA

0,02000   m o l   L - 1 em uma solução tamponada em p H   11,0 . Calcular os valores de   p S r

após a adição de 0,00 ;   10,00 ;   24,90 ;   25,00   e   25,10 de titulante.

Dados: α 4 = 0,85 ; K S r Y 2 - = 4,3 × 10 8 .

Passo 1

Temos uma titulação de S r 2 + 0,01000   m o l   L - 1 com EDTA 0,02000   m o l   L - 1 , a reação química envolvida é:

S r 2 + + Y 4 - → S r Y 2 -

O primeiro passo é calcular a constante de formação condicional:

K S r Y 2 - ' = K S r Y 2 - × α 4

O problema nos da α 4 = 0,85   e   K S r Y 2 - = 4,3 × 10 8 , vamos calcular então:

K S r Y 2 - ' = 4,3 × 10 8 × 0,85 = 3,7 × 10 8

Daqui pra frente a gente vai calcular o p S r para vários volumes de EDTA adicionado, então a gente precisa descobrir onde acontece o ponto de equivalência, para saber que tipo de cálculo empregar em cada caso:

V E D T A = V S r 2 + c S r 2 + c E D T A

Substituindo os dados, achamos:

V E D T A = 50,00   m L × 0,01000   m o l   L - 1 0,02000   m o l   L - 1 = 25,00   m L

O primeiro ponto que o problema pede é antes da adição de qualquer volume de EDTA, se a gente conhece a concentração da solução de S r 2 + que é igual a 0,01000   m o l   L - 1 , já podemos calcular o p S r para esse ponto!

Sabendo que:

p S r = - log ⁡ S r 2 +

Substituindo:

p S r = - 0,01000 = 2

Passo 2

Agora a gente quer o p S r para depois da adição de 10,00   m L de EDTA, esse ponto é antes do ponto de equivalência, logo temos que achar a concentração restante de S r 2 + , para isso fazemos:

S r 2 + = S r 2 + i n i c i a l × V S r 2 + -   E D T A × V E D T A V S r 2 + + V E D T A

Substituindo:

S r 2 + = 0,01000   m o l   L - 1 × 50,00   m L - 0,02000   m o l   L - 1 × 10,00   m L 50,00   m L + 10,00   m L

S r 2 + = 5,000 × 10 - 3

Agora é só calcular o p S r :

p S r = - 5,000 × 10 - 3 = 2,30

Passo 3

Para o V E D T A = 24,90   m L ainda estamos antes do P.E. então o cálculo é igualzinho ao passo anterior, só mudamos o volume de EDTA adicionado, então:

S r 2 + = 0,01000   m o l   L - 1 × 50,00   m L - 0,02000   m o l   L - 1 × 24,90   m L 50,00   m L + 24,90   m L

Achamos:

S r 2 + = 2,67 × 10 - 5

E calculamos o p S r :

p S r = - 2,67 × 10 - 5 = 4,57

Passo 4

Agora o volume de titulante adicionado é 25,00   m L , então estamos no ponto de equivalência!

A concentração de S r 2 + , pode ser calculada por:

S r 2 + = S r Y 2 - K S r Y 2 - '

A se todo o S r 2 + reagiu, então podemos calcular a concentração do complexo considerando a concentração do íon original:

S r Y 2 - = S r 2 + × V S r 2 + V T

Substituindo e calculando:

S r Y 2 - = 0,01000   m o l   L - 1 × 50,00   m L 50,00   m L + 25,00   m L = 6,667 × 10 - 3   m o l   L - 1

Agora podemos calcular a concentração do íon:

S r 2 + = 6,667 × 10 - 3 3,7 × 10 8 = 4,24 × 10 - 6   m o l   L - 1

E por fim o p S r :

p S r = - 4,24 × 10 - 6 = 5 , 37

Passo 5

Depois do ponto de equivalência a concentração do S r 2 + vem da dissociação do complexo, então podemos calcular:

S r 2 + = c S r Y 2 - c E D T A × K S r Y 2 - '  

Calculamos a concentração do S r Y 2 - :

c S r Y 2 - = 0,01000   m o l   L - 1 × 50,00   m L 50,00   m L + 25,10   m L = 6,6 67 × 10 - 3

E então substituimos para calcular a concentração do íon:

S r 2 + = 6,667 × 10 - 3   m o l   L - 1 0,02000   m o l   L - 1 × 4,3 × 10 8 = 7,74 × 10 - 10  

E finalmente o p S r :

p S r = - 7,74 × 10 - 10   = 9,11

Uhuuuul!!!

Resposta

V E D T A = 0,00   m L ;   p S r = 2

V E D T A = 10 , 00   m L ;   p S r = 2,30

V E D T A = 24 , 9 0   m L ;   p S r = 4,57

V E D T A = 25,00   m L ;   p S r = 5,37

V E D T A = 25,10   m L ;   p S r = 9,11

Exercícios de Livros Relacionados

Suponha que 15,0 mL de uma solução 0,15 M de NH3(aq) são titulados com uma solução 0,10 M de HCl(aq). (a) Qual é o pH inicial da solução 0,15 M de NH3 (aq)? (b) Qual é o pH após a adição de 15,0 mL de
Suponha que 25,0 mL de uma solução 0,10 M de CH3COOH(aq) são titulados com uma solução 0,10 M de NaOH(aq). (a) Qual é o pH inicial da solução 0,10 M de CH3COOH(aq)? (b) Qual é o pH após a adição de 10
Suponha que 50,0 mL de uma solução 0,25 M de CH3NH2(aq) são titulados com uma solução 0,35 M de HCl(aq). (a) Qual é o pH inicial da solução 0,25 M de CH3NH2(aq)? (b) Qual é o pH após a adição de 15,0
Suponha que 30,0 mL de uma solução 0,20 M de C6H5COOH(aq) são titulados com uma solução 0,30 M de NaOH(aq). (a) Qual é o pH inicial da solução 0,20 M de C6H5COOH(aq)? (b) Qual é o pH após a adição de
Que volume de uma solução 0,0848M de H C l ( a q ) deve ser adicionado a 88,8m L de uma solução 0,233M de N a 3 P O 4 ( a q ) para atingir (a) o primeiro ponto estequiométrico; (b) o segundo ponto est