Titulação Redox
Teoria
Na titulação redox, como o próprio nome já sugere, acontece uma reação de oxirredução entre o analito, titulado e a solução padrão de concentração conhecida, o titulante!
Vamos considerar uma titulação redox de de uma solução de que em meio ácido, gastou de uma solução padrão de .
Qual é a concentração de ?!
Bem, nesse caso o anaito é o e para acharmos sua concentração a gente vai calcular a conentração de !
Quando adicionamos a solução de no erlenmeyer a reação que acontece é essa daqui:
O que temos é o cério reduzindo de para e o ferro oxidando de para , se o cério esta ganhando um elétron e o ferro esta perdendo um, então dizemos que a proporção de , precisamos de um mol de para oxidar um mol de !
Pra entendermos o porque que o célio reduz e o ferro oxida, podemos dar uma olhada nas suas semi reações de redução:
Como podemos ver, o potencial padrão do célio é maior que o do ferro!
Mas a gente queria saber a concentração de , certo?!
Lá em cima vimos que foi necessário de titulante para titular de solução contendo íons de ferro, este é portanto o ponto de equivalência. Nesse momento todo o foi oxidado a e por concequência o reduziu a , logo:
Se o número de mols é a concentração vezes o volume...
Isolando a concentração de íons de ferro:
Substituindo achamos a concentração de incial:
Curva de Titulação
A curva de titululação redox tem a mesma carinha que as outras curvas de titulação, no eixo temos o volume do titulante adicionado em maaas no eixo ao invés de ter uma função logarítima (tipo , ) a gente tem o potencial de redução em volts!
Então porque ela tem a mesma forma que as outras curvas de titulação?!
Você lembra da equação de Nernst?!
Vamos usar ela pra calcular o potencial para cada volume de titulante adicionado e ela também é uma função logarítima!!
A curva de titulação vai ter 3 regiões, antes do ponto de equilíbrio, no ponto de equilíbrio e depois do ponto de equilíbrio. Bora aprender a calcular?!
Antes do ponto de equivalência
No primeiro momento tudo que temos é a nossa solução de íons de ferro bonitinha no erlenmeyer onde teoricamente só tem ! E porque teoricamente?!
Porque o ferro também reage com o oxigênio e oxida! Porém aqui a gente vai fazer de conta que isso não acontece, beleza?!
Antes do ponto de equivalência não vamos ter nenhuma concentração de , porque todo o cério adicionado vai reagir imediatamente reduzindo a , portanto vamos fazer...
Então vamos calcular o potencial do sistema depois da adição do titulante! Montamos a equação:
Como o e o estão dentro de uma mesmo volume, podemos simplificar essa equação:
O número de mols de vai ser o que restou, para isso subtraimos o número de mols de adicionado:
E o número de mols de , por sua vez, vai ser igual ao número de mols de adicionado:
Para a adição de de de , temos:
E também...
Substituindo na equação, achamos:
Maaas, o número de mols inicial de vai ser sempre a mesma, certo?! A concentração do titulante também, não é?!
Então podemos montar uma equação que vai servir para qualquer volume antes do ponto de equivalência:
Dessa forma só precisamos ter o trabalhão uma vez!!
No ponto de equivalência
Agora vamos para o ponto de equivalência, que como vimos lá em cima acontece ao adicionar de titulado!
Podemos escrever o potencial no equilíbrio, como:
Ou:
No ponto de equivalência, também temos:
Então podemos somar as duas equações...
E ficamos com:
Isolando o potencial do equilíbrio:
Agora é só substituir os potenciais padrão de cada semi reação:
E é isso!!
Depois do ponto de equivalência
Depois do ponto de equivalência temos a situação contrária ao antes de p.e., se antes não tinhamos nada de agora não temos nada de , porque todo ele foi oxidado!
Calculamos o potencial do par então:
Da mesma forma que fizemos lá e cima..
Beleza, temos que calcular esses números de mols!
Todo o vem da oxidação do ferro, então podemos dizer que:
Substituindo e calculando:
Esse valor nunca vai mudar, beleza?! Não importa se adicionamos ou do titulante!
Agora o número de mols de , vai ser referente ao excesso, vamos supor uma adição de de titulante:
Calculando:
Substituindo achamos o potencial:
Da mesma forma que fizemos o esqueminha lá em cima para qualquer volume, podemos fazer aqui, ficariamos com:
Se fizemos vários pontos o gráfico vai ficar assim:
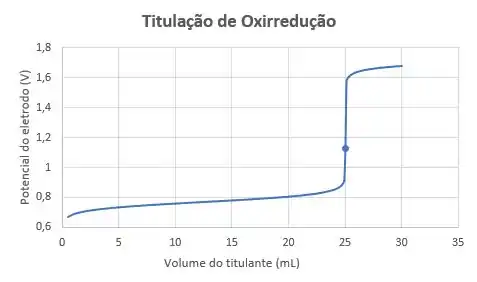
Agora a gente se ve nos exercícios!
Curva de Titulação
Antes do ponto de equivalência
No ponto de equivalência
Depois do ponto de equivalência
Exercícios Resolvidos
Exercício Resolvido #1
Lista de Química Analítica II-UFF
Um mineral contendo ferro foi dissolvido, o ferro reduzido a e, a solução resultante foi titulada com padrão de . A reação é a seguinte:
Com base nos seguintes dados, determine a percentagem de na amostra:
- Massa da amostra
- Volume de gasto
- Molaridade de
Passo 1
O problema da pra a gente a reação de oxirredução, então vemos que o ferro esta se oxidando e o permanganato reduzindo!
E a gente quer ver quanto de ferro tem nessa amostra, certo?!
Pela estequiometria, no ponto de equivalência, vamos ter:
Escrevendo o número de mols do titulante em função da sua concentração e do volume utilizado para chegar no ponto de equivalência:
Substituindo os dados do problema:
Calculando, achamos:
Passo 2
Beleza, mas a gente quer a porcentagem de , então vamos pensar lá no inicio, quando a amostra foi dissovida!
Para cada mol de foram gerados dois mols de que depois foi reduzido a e ai sim a titulação começou! Então temos:
Logo:
Podemos calcular a massa de sabendo que :
Achamos:
Passo 3
E finalmente podemos achar a porcentagem de na amostra, lembrando que a massa da amostra é de :
Substituindo:
Calculando:
Aweeee!!!
Resposta
Exercício Resolvido #2
Lista de Química Analítica-UCBR
Uma quantidade de um minério de ferro igual a foi dissolvida e passada
por um redutor de Jones. A titulação do produzido necessitou de
de Expresse os resultados dessa análise em termos de porcentual de.
Passo 1
Primeiro de tudo, você deve estar se perguntando o que é redutor Jones! Certo?!
A verdade é que não importa muito, porque pelo contexto ele ta reduzindo o ferro contido na solução analisada a , show?!
Maaas, só a título de curiosidade ele é um dispositivo usado para reduzir íons metálicos usando amálgama de zinco.
Agora vamos para a questão em si!
Temos uma solução de sendo titulada com , permanganato é um forte agente oxidante, então já da pra imaginar o que vai acontecer com o ferro, né..
Mas vamos cosultar uma tabelinha e achar as semi reações, junramente com seus !
Como podemos ver o potencial de redução do é bem maior que o do ferro! Mas enquanto a reação do permanganato precisa de mols de elétrons para acontecer, a reação do ferro só precisa de um!
Vamos ter que arrumar isso daí!!!
Para escrever a reação global vamos inverter a reação do já que ele esta se oxidando e multiplicar ela por :
Passo 2
Mas a titulação foi feita pra descobrimos o percentual de ferro, certo?!
Foi preciso de de pra reduzir uma solução feita com de minério. Com esse volume temos uma equivalência de números de mols, mas cada mol de permangato oxida mols de , então:
Sabendo que:
Podemos substituir e calcular o número de mols de íons de ferro:
Ou:
Passo 3
Agora que a gente sabe a quantidade de ferro em mols é só descobrir quantas gramas, para isso precisamos da massa molar do ferro:
E fazemos:
Substituindo:
Agora podemos achar seu percentual, afinal:
Lembrando que a massa de minério de ferro era de , então:
Finalmente...
Viiu, nem é tão difícil!!
Resposta
Exercício Resolvido #3
Lista de Análises Químicas Quantitativas-UNICHIETA
Qual é a porcentagem de ferro em um arame se, após a dissolução de uma amostra de desse arame em , ao abrigo do ar, se gastaram de uma solução padrão de para titular o ferro até rosa claro?
Passo 1
Vamos lá!!
A primeira coisa que acontece é a dissolução da amostra de ferro em , para isso acontece a seguinte reação:
No sulfato de ferro temos o ferro com , que vai ser titulado com permanganato de potássio, que é um forte agente oxidante...esperamos então que o ferro oxide e o permanganato reduza, mas vamos escrever as semi reações com seus potenciais padrão de redução para conferir:
O potencial de redução do é maior, como imaginávamos!
Agora podemos escrever a reação global:
No ponto de equivalência temos a seguinte relação:
Passo 2
O problema diz que foi gasto de uma solução padrão de para a reação ficar rosa claro, marcando o ponto de equivalência!
Podemos reescrever a realção acima:
Substituindo os dados:
Passo 3
Com isso podemos calcular a massa de ferro na amostra:
Se , então:
Calculando:
Se a amostra tem , então a porcentagem de ferro é:
Achamos:
Uhuuul!!!
Resposta
Exercício Resolvido #4
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 20 , exercício 20-44.
Uma amostra contendo contendo o mineral telurita foi dissolvida e tratada com
de :
Quando a reação se completou, o excesso de consumiu na retrotitulação
com . Calcule a porcentagem de na amostra.
Passo 1
Beleza, então aqui estamos trabalhando com duas reações de oxirredução! Vamos organizar as informações então!!
Temos uma amostra contendo , essa amostra foi dissolvida e queremos descobrir quanto de tem nessa amostra em termos de porcentagem!
Para isso adicionamos de que vai reagir com a telurita da seguinte forma:
O vai do NOX para o NOX , portanto oxida, enquanto o cromo vai de para , conferindo vemos que a equação ta balanceada, então tudo certo!
Temos a seguinte relação no ponto de equivalência:
Passo 2
O problema é que não conhecemos o volume de no ponto de equivalência, afinal ele foi adicionado em excesso!!
Mas esse excesso foi titulado com e esperamos a seguinte reação:
No ponto de equivalência, temos:
Se o número de mols é a concentração multiplicada pelo volume, temos:
O problema diz que o excesso de consumiu de , então:
Passo 3
Conhecemos o excesso de dicromato, então podemos dizer que:
Onde é o número de mols gasto no primeiro procedimento, é ele que queremos conhecer! Isolando:
Agora substituindo a concentração e o volume de dicromato:
Substituindo os dados:
Calculando:
Passo 4
Agora sim, podemos voltar na relação entre o e o :
Isolando o número de mols de e substituindo:
Agora podemos calcular a massa de , sabendo que :
Calculamos:
E finalmente a porcentagem de na amostra contendo :
Achamos:
Prontinho!!!
Resposta
Exercício Resolvido #5
de uma solução de foram titulados com . Considerando que a do meio é e, constante durante a titulação, determine o potencial de eletrodo após adição de do titulante, no ponto de equivalência e, após adição de do titulante. A reação que se processa é:
E que os valores dos potenciais de redução:
Respostas; 0.767; 1.39 e 1.51
Passo 1
Vamos lá!
Primeiro precisamos saber onde fica o ponto de equivalência pra poder saber se com de titulante já chegamos lá!
No ponto de equivalência temos:
O que fica:
Isolando o volume:
Substituindo:
Calculando, achamos:
Beleza, então ainda não chegamos lá!
Passo 2
Para o cálculo do potencial antes do ponto de equivalência, fazemos:
Precisamos calcular os números de mols, então vamos lá:
Substituindo:
Agora do :
Agora é só substituir tudo na equação de Nernst e correr pro abraço:
Calculando, achamos:
Aweee!!!