Equação de Nernst
Produzido por Marcelo BrillantinoTeoria
Bora aprender a usar a Equação de Nernst de uma vez por todas?!
O que é a equação de Nernst?
Vamos direto ao ponto! A Fórmula de Nernst tem essa carinha aqui:
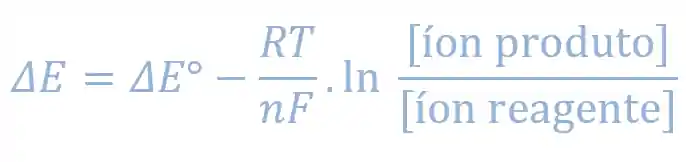
Onde:
é a diferença de potencial da pilha em ; é ddp da pilha em condições padrão, isso é e é a constante dos gases ideais, igual a ; -
é a temperatura em é o número de mols de íons envolvido na reação; - E
é a constante de Faraday, igual a
Pra que Serve a Equação de Nernst?
A Equação de Nernst vai nos ajudar em muitos momentos! Como no cálculo de
Isso mesmo, a Equação de Nernst serve pra calcular o ddp de uma pilha com diferentes concentrações e em diferentes temperaturas, ou seja, fora das condições padrão de
Durante o funcionamento da pilha ocorre uma reação de oxirredução, como essa daqui de baixo:
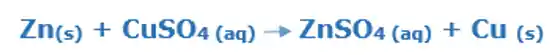
Temos um metal sofrendo oxidação e um cátion sofrendo redução, podemos dividir essa reação em duas semirreações:
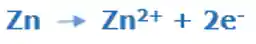
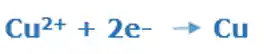
O íon do produto vai ser o anodo,
Equação de Nernst simplificada
Existe uma forma simplificada da Fórmula de Nernst, mas ela só vale para soluções à
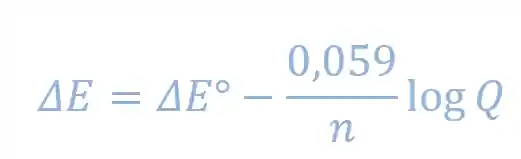
Onde
Confira nesse vídeo abaixo um resumo super completo sobre a Equação de Nernst! 👇
📢 Clique para ver mais:
Como usar a equação de Nernst?
A equação de Nernst é muito utilizada para o cálculo do
Exemplo: Uma mistura ácida de
A primeira coisa que fazemos é escrever a reação química:
Bom, pra achar o pH precisamos da concentração de
Substituindo os dados:
Agora a gente calcula isso tudo e chegamos a:
Lembrando que:
Resolvendo:
O
Agora vamos praticar com exercícios?!
Como usar a equação de Nernst?
Exercícios Resolvidos
Exercício Resolvido #1
IFSUL – Material de Aula de Físico-Química. Prof. Marcelo Alves.
a) Qual a de uma pilha de e em condições padrão no instante em que ela começa a funcionar?
b) Qual a da mesma pilha após certo tempo de funcionamento, quando e ?
Dados: e
Passo 1
a) Com os potenciais padrão do zinco e do cobre, a gente vê que em uma pilha desses caras, o cobre (potencial de redução maior) vai sofrer redução e o zinco vai sofrer oxidação (potencial de redução menor).
Atenção: o cobre possui cátions e , mas o potencial dado é da reação do indo para .
Reação global:
E o cálculo da :
Passo 2
b) Fora das condições padrão, precisamos usar a equação de Nersnt:
Viu? Trocamos por 8,314 J/molK; por 298 K, que equivale a 25°C; por 2, porque nas reações REDOX existem 2 elétrons e pela constante de Faraday.
Pela reação global, a gente vê quem é o íon nos produtos e quem é o íon nos reagentes.
E esse exercício nos mostra que, conforme a pilha funciona, ela vai sendo “gasta”. Ou seja, o potencial (a voltagem) oferecida vai diminuindo. Até que a reação se esgota.
Resposta
a) 1,10 V
b) 1,09 V
Exercício Resolvido #2
IQSC-USP. Lista de Eletroquímica. Questão 09.
Calcule para as seguintes pilhas:
a)
b)
c)
d)
Passo 1
Vamos precisar de uma tabela com todos esses potenciais!
Como o enunciado nos diz que são pilhas, sabemos que todas as reações são espontâneas.
Vamos ter que calcular o de cada pilha e, com a equação de Nersnt, mudar de para o nas concentrações dadas.
Vamos considerar a temperatura de 25°C (298 K) e a equação de Nersnt completa. Talvez seu professor utilize a equação simplificada. Nesse caso, basta aplicar:
Sendo e o mesmo número de elétrons que usamos na equação completa.
Passo 2
a)
Aplicando a equação de Nersnt:
Passo 3
b)
Aplicando a equação de Nersnt:
Passo 4
c)
Aplicando a equação de Nersnt:
Passo 5
d)
Aplicando a equação de Nersnt:
Resposta
a) 1,07 V
b) 0,14 V
c) 0,64 V
d) 0,46 V
Exercício Resolvido #3
UERJ – Lista de Eletroquímica. Prof. Nilson Bispo. Questão 02.
Calcule a tensão produzida a 25°C pela célula:
Se e .
Passo 1
Numa tabela de potenciais de redução, a gente pode buscar os potenciais desses caras, assim:
Passo 2
Pelo diagrama da pilha, a gente vê que o anodo é o eletrodo de estanho e o catodo é o de prata. Portanto, a reação do estanho é de OXIDAÇÃO.
Vamos inverter a reação do estanho e o sinal do potencial dele:
Você pode “pular” o passo 1. Só fizemos assim porque na maioria das tabelas o potencial exposto é o de redução, e queríamos chamar sua atenção pro fato de que, se a reação é de oxidação, o sinal troca, beleza?
Passo 3
Agora, pra reação global, precisamos igualar o número de elétrons. Multiplicamos a reação de redução da prata por 2, SEM MULTIPLICAR O VALOR DO POTENCIAL. E somamos tudo pra achar o potencial da pilha nas condições normal (25°C e concentrações de 1,0 molar).
Reação global:
Passo 4
Como as concentrações são diferentes de 1,0 molar, precisamos usar a equação de Nersnt pra calcular o potencial, a partir daquele ali que calculamos.
Pela equação completa:
Calculamos o como 0,94 V, o vai ser aquele 2, dos 2 elétrons que cortamos na reação global. O íon produto, pela reação global, é o e o íon reagente é o , cujas concentrações foram dadas no enunciado.
Lembrando que , é a temperatura em Kelvin ) e a constante de Faraday é ... hora de calcular:
E aquele “ao quadrado” ali na prata é porque, na reação global, ela aparece com coeficiente 2, beleza?
Pela equação simplificada:
Feshow.
Resposta
0,98 V
Exercício Resolvido #4
UDESC – Química Geral e Inorgânica. Prof. Carla D. Lista de eletroquímica. Questão 08.
Uma célula de concentração é formada por dois pares redox idênticos, no catodo e no anodo, em diferentes concentrações de íons nos respectivos compartimentos. Calcule o potencial gerado pelas seguintes células de concentração.
a) Uma barra de mergulhada numa solução contendo de em contato elétrico com outra barra de , mergulhada numa solução contendo de .
b) Um metal inerte, como a platina (), mergulhada numa solução ácida de , em contato elétrico com outro eletrodo de platina, mergulhado numa solução ácida de . Ambas soluções contem sob pressão de 1 bar. Dica:
Passo 1
Primeiro de tudo e antes de mais nada, vamos entender essa história aí de pilha de concentração.
Antes da gente ver a equação do seu Nersnt, pra formar a pilha nós precisávamos de dois materiais com potenciais diferentes. Essa “ddp” entre eles justificava o funcionamento da pilha galvânica.
Agora, a gente já é gente grande da eletroquímica, e já tá ligado que diferenças nas concentrações alteram os potenciais das pilhas.
Uma consequência disso, é que podemos formar pilhas de concentração, onde temos um só metal nos dois eletrodos. Pra que a pilha funcione, usamos concentrações diferentes nas soluções de cada semi-célula.
Pra esses casos, o potencial da pilha é calculado por:
Antes de ficar quebrando cabeça, vamos ver como usamos isso na prática!
Passo 2
a) Em pilhas com diferentes eletrodos, nós calculamos o e, depois, transformamos em pela equação de Nersnt.
No entanto, numa pilha de concentração, a reação global é totalmente “zerada”. Olha só, no caso do cobre se oxidando no anodo e se reduzindo no catodo:
A global seria:
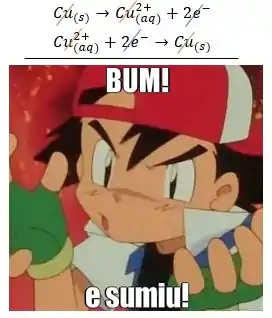
Tudo foi “cortado”.
Pra evitar esse problema, aplicamos Nersnt nas semirreações, e não na reação global!
Passo 3
Primeiro vamos descobrir em qual compartimento teremos a oxidação: o de menor concentração ou o de maior concentração de ?
Reação normal:
Aplicando Nersnt nessa reação:
O nosso produto da reação, não é um íon! É o ! Como ele não está em fase aquosa, a gente usa na fórmula.
Para a célula de menor concentração de íon:
Para a célula de maior concentração de íon:
O que a gente descobre com isso?
Quem tem MAIOR POTENCIAL DE REDUÇÃO vai SOFRER REDUÇÃO.
O que nossos cálculos aí de cima mostraram é que na célula com MAIOR concentração, temos o MAIOR POTENCIAL DE REDUÇÃO.
Conclusão:
Isso sempre acontece ok? Em célula de concentração o anodo vai ser o de menor concentração.
Beleza?
Então, pro nosso exercício aqui:
E a diferença de potencial da célula será:
Pra usar a outra fórmula:
A representação da reação global da pilha pode ser feita assim:
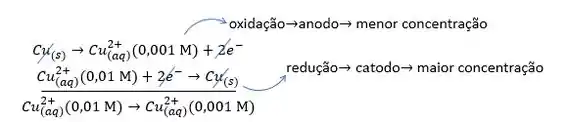
Atenção: os potenciais que calculamos com a equação de Nersnt são de redução porque nossa baseamos na reação de redução e no potencial de redução!
Passo 4
b) Parece complicado, mas é a mesma coisa.
A platina não entra no jogo, afinal ele é inerte.
Temos uma pilha de concentração, onde no catodo teremos a seguinte reação:
E no anodo:
Então precisamos saber onde teremos o catodo e onde teremos o anodo.
Para :
Para p:
Como e já sabemos que na semi-célula de menor concentração teremos o anodo, podemos dizer que:
Sendo a reação global:
Passo 5
Em pilhas de concentração, então, precisamos aplicar Nersnt em cada semi-célula pra descobrir seus potenciais fora das condições normais.
Dada a reação de redução:
Pra concentração de M:
Pra concentração de M:
Confirmando o que já sabíamos: na semi-célula com M temos menor potencial de redução, portanto ocorrerá a oxidação e ela será o anodo.
O potencial da pilha será, então:
Você pode, claro, inverter a reação do anodo no sentido de oxidação e fazer as contas com o potencial de oxidação.
Também podemos usar a reação global, olha só:
A matemática e a química são duas lindas né? Não importa o caminho, importa chegarmos lá!
Resposta
a)
b)
Exercício Resolvido #5
James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 639 exercício 17.86
Um eletrodo de imerso numa solução 1,0 mol/l de tem um potencial padrão de redução de +022 V
Um segundo eletrodo é imerso numa solução contendo íons cloreto em uma concentração desconhecida. A pilha apresenta um potencial de 0,0435 V, com o eletrodo da solução desconhecida servindo de anodo. Qual a concentração molar desconhecida do ?
Passo 1
Usando os conceitos de potencial.
O potencial da pilha medida é obtido pelo seguinte cálculo:
Aplicando os valores teremos:
Que pode ser simplificado para:
Passo 2
A equação de Nernst.
A equação de Nernst para esse problema fica assim
Substituindo os valores teremos:
Que resolvendo encontramos:
Assim a concentração de Cl- será dada pela seguinte conta:
Logo
Resposta
Exercício Resolvido #6
IQSC – USP – Lista de Eletroquímica. Questão 08.
Calcule as constantes de equilíbrio para as seguintes reações de pilhas:
a)
b)
c)
Passo 1
Vamos recapitular:
Precisamos calcular o das pilhas e depois jogar nessa fórmula:
Pra encontrar o valor de .
Partiu?
Passo 2
a)
Reação global:
Para a constante:
Passo 3
b)
Reação global:
Para a constante:
Passo 4
c)
Reação global:
Para a constante:
Resposta
a)
b)
c)
Exercício Resolvido #7
USJT – Aula de Eletroquímica. Exemplo de aula.
Calcular a constante de equilíbrio da reação:
Temperatura: 25°C.
Passo 1
Não se desespera! Essa é uma questão diferente, mas não é difícil. É só a gente entender o que tem que fazer.
A constante desse equilíbrio aí de cima, é a constatante de solubilidade do cloreto de prata.
O cloreto de prata é um cara insolúvel, o que significa que sua constante de solubilidade é bem baixa, ok? Então, estamos procurando um valor de pequeno.
Passo 2
A reação de solubilidade do cloreto de prata NÃO É uma reação REDOX.
Mas a gente pode “desmanchar” ela em duas etapas REDOX, olha só:
Somando essas duas reações, teríamos a reação global:
Não importa se essas duas etapas não acontecem na “vida real”. O caminho pra chegar no final não importa, ok? Importa o início () e o final (os íons dissociados).
E, olhando numa tabelinha de potenciais, encontramos que:
Portanto, o da reação global será:
Beleza, potencial da célula calculado!
Passo 3
E, lá na nossa teoria, a gente viu uma relação enter o e o :
Portanto:
Resposta