Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 10.Questões e Problemas - Ex. 14d

Calcule o erro relativo porcentual na solubilidade devido ao uso de concentrações em vez de atividades para os seguintes compostos presentes em K N O 3   0,05000   m o l   L - 1 utilizando os produtos de solubilidade termodinâmicos listados no Apêndice 2.

  1. L a ( I O 3 ) 3 .

Passo 1

Oi galera, vem comigo! Primeiramente precisamos da reação química e o produto de solubilidade do iodato de lantânio:

L a ( I O 3 ) 3 ⇌ L a 3 + + 3 I O 3 -                                           K p s = 1,0 ∙ 10 - 11

Quando a gente desconsidera as atividades no cálculo da solubilidade, temos o seguinte:

K p s = L a 3 + [ I O 3 - ] 3 = 1,0 ∙ 10 - 11

Pela estequiometria da reação, temos:

L a 3 + = S

Além disso, para 1 mol de L a 3 + temos 3 mols I O 3 - , ou seja:

I O 3 - = 3 ∙ L a 3 + = 3 ∙ S

Substituindo na equação de K p s , vamos ter o seguinte:

S ∙ ( 3 ∙ S ) 3 = 1,0 ∙ 10 - 11

27 ∙ S 4 = 1,0 ∙ 10 - 11

S = 1,0 ∙ 10 - 11 27 4 = 7,80 ∙ 10 - 4   m o l / L

Passo 2

Se considerarmos as atividades no cálculo da solubilidade:

K p s ' = K p s γ L a 3 + ∙ γ I O 3 - 3 = L a 3 + [ I O 3 - ] 3

Mas antes precisamos calcular a força iônica, e vamos usar a seguinte equação:

μ = 1 2 ( [ A ] ∙ Z A 2 + [ B ] ∙ Z B 2 + [ C ] ∙ Z C 2 + … )

Onde:

  • [ A ] , [ B ] , [ C ] , ... representam as concentrações molares de espécie dos íons A, B, C, ...
  • Z A 2 , Z B 2 , Z C 2 , ... correspondem às cargas da sua espécie

A força iônica a partir de K N O 3   0,05000   m o l   L - 1 será:

K N O 3 ⇌ K + + N O 3 -

μ = 1 2 K + ∙ 1 2 + N O 3 - ∙ 1 2 = 1 2 0,05000 + 0,05000 = 0,05   m o l / L

No cálculo de μ , consideramos que os íons L a 3 + e I O 3 - provenientes do precipitado não afetam significativamente a força iônica da solução.

Passo 3

Pela Tabela com uma força iônica de 0,05   m o l / L , conseguimos encontrar o coeficiente de atividade ( γ ):

γ L a 3 + = 0,24

γ I O 3 - = 0,81

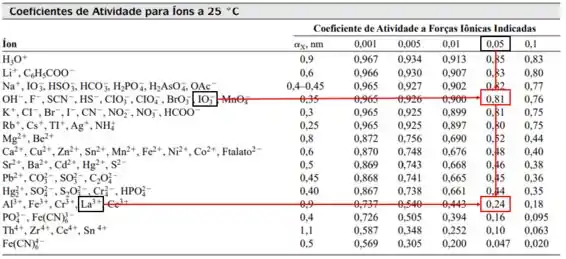
Voltando na equação de K p s ' :

K p s ' = K p s γ L a 3 + ∙ γ I O 3 - 3 = 1,0 ∙ 10 - 11 0 , 24 ∙ 0,81 3

K p s ' = 7,84 ∙ 10 - 11

Sendo assim, temos:

K p s ' = L a 3 + [ I O 3 - ] 3 = 7,84 ∙ 10 - 1 1

Como vimos no Passo 1:

L a 3 + = S ;

I O 3 - = 3 ∙ S .

Substituindo:

27 ∙ S 4 = 7,84 ∙ 10 - 11

S = 7,84 ∙ 10 - 11 27 4 = 1 , 31 ∙ 10 - 3   m o l / L

Passo 4

Agora precisamos calcular o erro relativo percentual, onde:

x v = 1,31 ∙ 10 - 3   m o l / L ;

x i = 7,80 ∙ 10 - 4   m o l / L .

E r = x i - x v x v ∙ 100 % = 7,80 ∙ 10 - 4 - 1,31 ∙ 10 - 3 1,31 ∙ 10 - 3 ∙ 100 %

E r = - 40 %

Prontinho pessoal, até mais!

Resposta

E r = - 40 % .

Exercícios de Livros Relacionados

A forma da equação de Scatchard dada no Impacto 15.2 se aplica somente quando a macromolécula tem sítios de ligação independentes e equivalentes. Para sitios de ligação independentes e não-equivalente
Para o equilíbrio C a F 2 ( s ) ⇌ C a 2 + ( a q ) + 2F - ( a q ) , K = 3,9 × 10 - 11 , a 25° C , e a energia de Gibbs padrão de formação do C a F 2 ( s ) é - 1167k J.m o l - 1 . Calcule a energia de G
Para o equilíbrio P b I 2 s ⇌ P b 2 + ( a q ) + 2I - ( a q ) , K = 1 , 4 × 10 - 8 , a 25° C , e a energia de Gibbs padrão de formação do P b I 2 s é - 173,64k J.m o l - 1 . Calcule a energia de Gibbs
Calcule a força iônica de uma solução que é 0,1m o lk g - 1 em K C l (aq) e 0,2m o l k g - 1 em C u S O 4 ( a q ) .
Calcule a força iônica de uma solução que é 0,04m o lk g - 1 em k 3 F e C N 6 a q ,0,030m o l k g - 1 em K C l ( a q ) e 0,050m o lk g - 1 em N a B ra q .