Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 21.Questões e Problemas - Ex. 23
Calcule o potencial de um eletrodo indicador de prata versus um eletrodo de calomelano saturado, após a adição de 5,00; 15,00; 25,00; 30,00; 35,00; 39,00; 39,50; 39,60; 39,70; 39,80; 39,90; 39,95; 39,99; 40,00; 40,01; 40,05; 40,10; 40,20; 40,30; 40,40; 40,50; 41,00; 45,00; 50,00; 55,00; e 70,00 mL de AgNO3 0,1000 mol L1 a 50,00 mL de KSeCN 0,0800 mol L1. Construa uma curva de titulação e um gráfico com a primeira e segunda derivadas desses dados. (Kps para o AgSeCN 4,20 1016.)
Passo 1
Titulação de KSeCN com é uma titulação de precipitação. Temos três regiões de titulação:
Antes do ponto de equivalência
No ponto de equivalência ⇒ [] é calculado a partir de
Após o ponto de equivalência ⇒ [] é igual ao excesso de concentração de prata
Lembre-se que o potencial da célula é calculado da seguinte maneira:
Em nossa tarefa, o eletrodo de prata é o eletrodo indicador e o eletrodo de calomelano padrão é o eletrodo de referência, então podemos escrever:
Lembre-se que o potencial dos eletrodos indicadores metálicos (eletrodo de prata) pode ser calculado usando esta equação:
Portanto, para calcular o potencial do eletrodo de prata, precisamos calcular a concentração de em cada volume adicionado à solução KSeCN.
Passo 2
Antes do ponto de equivalência.
Antes do ponto de equivalência, KSeCN está em excesso, então precisamos calcular sua concentração primeiro:
Mols de KSeCN são iguais à subtração de mols iniciais de KSeCN e mols de adicionado:
Só vamos calcular a concentração de KSeCN quando 5,00 mL de é adicionado e o restante no programa de computador.
Concentração de KSeCN a 5 mL de adicionado:
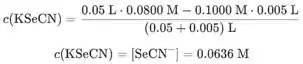
Agora podemos calcular a concentração de a 5 mL usando o produto de solubilidade do AgSeCN que é observado na tarefa:
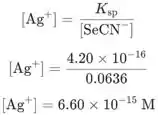
Calcule todas as concentrações até o ponto de equivalência desta forma no programa de computador.
Agora podemos usar a equação do passo 3 para calcular o potencial da célula:
Encontre os potenciais de redução padrão do eletrodo de prata e do eletrodo de calomelano padrão no Apêndice 5 e calcule E da célula:
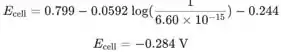
Calcule todos os outros potenciais usando esta equação no programa de computador.
No ponto de equivalência.
No ponto de equivalência, as concentrações de e são iguais, então podemos usar a equação do produto de solubilidade para calcular suas concentrações:
Concentrações de e são iguais, então podemos escrever:
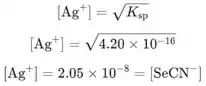
O potencial da célula no ponto de equivalência é:
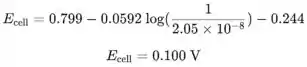
Passo 3
Após o ponto de equivalência
Por último, temos que calcular o potencial após o ponto de equivalência. Há excesso de na solução para que possamos calcular sua concentração desta forma:
Mols de são iguais à subtração de mols de adicionados e mols de KSeCN inicial:
Vamos apenas calcular a concentração de no primeiro volume após o ponto de equivalência (40,01 mL) e o restante no programa de computador.
Concentração de na adição de 40,01 mL é:
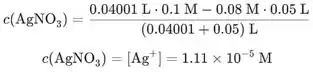
Calcule todas as outras concentrações de após o ponto de equivalência desta forma.
Agora podemos usar a equação da etapa 3 para calcular o potencial da célula em 40,01 mL de adicionado:
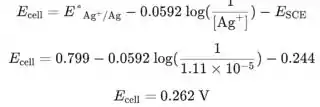
Calcule todos os outros potenciais usando esta equação no programa de computador.
As fórmulas que vamos usar para a primeira curva de titulação estão anotadas em D2, E2 e F2. As fórmulas que vamos usar para o gráfico da primeira derivada estão em G3, H3, I3 e J3. As fórmulas que vamos usar para o gráfico da segunda derivada estão em K4, L4, M4 e N4:
Os dados que vamos usar para a curva de titulação são:
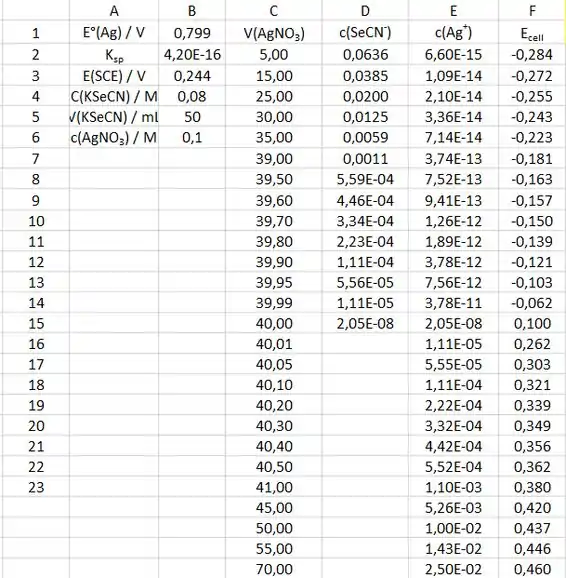
Para a primeira curva de titulação, colocaremos o volume de no eixo x e o potencial da célula no eixo y. A curva de titulação fica assim:
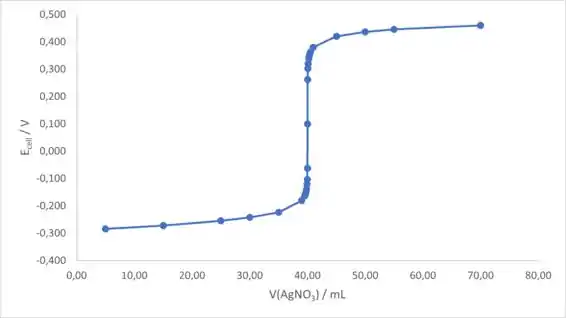
Os dados que vamos usar para o gráfico da primeira e segunda derivada são:
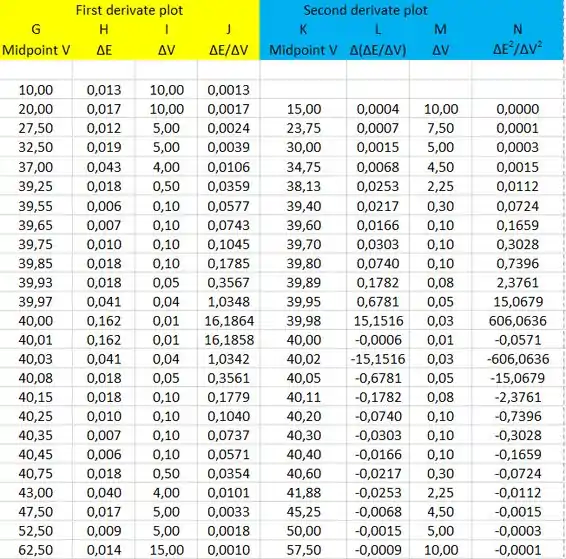
Para o gráfico da primeira derivada, colocaremos o volume de (coluna C) no eixo x e o ΔE/ΔV (coluna J) no eixo y. O gráfico da primeira derivada é:
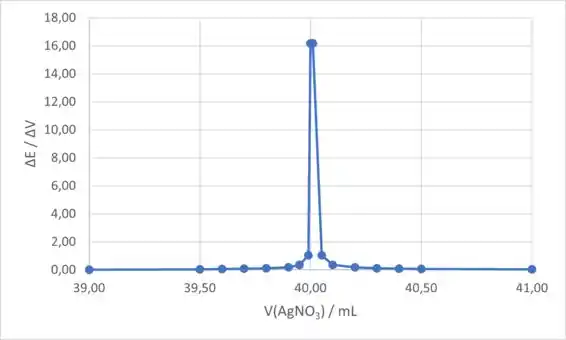
Para o gráfico da segunda derivada, colocaremos o volume de (coluna C) no eixo x e o (coluna N) no eixo y. O gráfico da segunda derivada é:
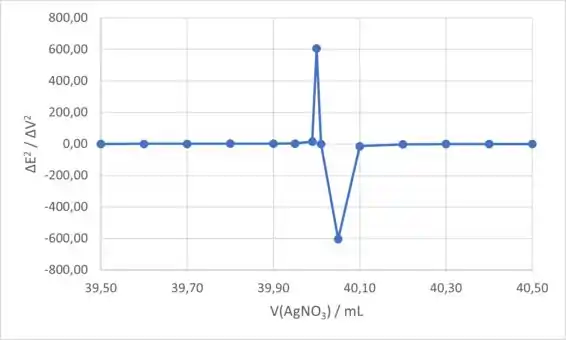
Resposta
Ver todo o desenvolvimento