Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 11.1 - Ex. 87
Calcule o pH das seguintes soluções de ácidos dipróticos, em 25°C. Ignore a segunda desprotonação somente quando a aproximação for justificada: a) 0,010 M de H2CO3 (aq); b) 0,10 M de (COOH)2 (aq); c) 0,20 M de H2S (aq).
Passo 1
Os Ka foram obtidos na Tabela 11.10 do livro.
Passo 2
Letra a)
A primeira equação de desprotonação do H2CO3 se dá:
Temos que Ka1 é:
Ka1 = 4,3x10-7
Devemos construir a Tabela de Equilíbrio e analisá-la:
Precisamos calcular x para obtermos H3O+ no equilíbrio, então:
Aplicando a fórmula de bhaskara, temos que:
Adotaremos uma faixa de 10% de desprotonação em relação à concentração inicial, ou seja, se x > 10% devemos considerar a segunda desprotonação, do contrário, não.
Nesse caso, x = 0,654%, desconsidera-se a segunda desprotonação.
Finalmente, o cálculo de pH se dá:
Passo 3
Letra b)
A primeira equação de desprotonação do (COOH)2 se dá:
Temos que Ka1 é:
Ka1 = 5,9x10-2
Devemos construir a Tabela de Equilíbrio e analisá-la:
Precisamos calcular x para obtermos H3O+ no equilíbrio, então:
Aplicando a fórmula de bhaskara, temos que:
Adotaremos uma faixa de 10% de desprotonação em relação à concentração inicial, ou seja, se x > 10% devemos considerar a segunda desprotonação, do contrário, não.
Nesse caso, x = 52,8%, não se desconsidera a segunda desprotonação.
Para a segunda desprotonação temos a seguinte equação:
Temos que Ka2 é:
Ka1 = 6,5x10-5
Devemos construir a Tabela de Equilíbrio e analisá-la:
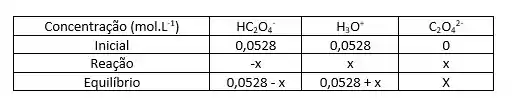
Precisamos calcular x:
Aplicando a fórmula de bhaskara, temos que:
A concentração de H3O+ se dá pela soma de suas concentrações obtidas na primeira e segunda desprotonação:
Finalmente, o cálculo de pH se dá:
Passo 4
Letra c)
A primeira equação de desprotonação do H2CO3 se dá:
Temos que Ka1 é:
Ka1 = 1,3x10-7
Devemos construir a Tabela de Equilíbrio e analisá-la:
Precisamos calcular x para obtermos H3O+ no equilíbrio, então:
Aplicando a fórmula de bhaskara, temos que:
Adotaremos uma faixa de 10% de desprotonação em relação à concentração inicial, ou seja, se x > 10% devemos considerar a segunda desprotonação, do contrário, não.
Nesse caso, x = 0,081%, desconsidera-se a segunda desprotonação.
Finalmente, o cálculo de pH se dá:
Resposta
a) 4,18;
b) 1,28;
c) 3,79.