Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 5.Questões e Problemas - Ex. 12
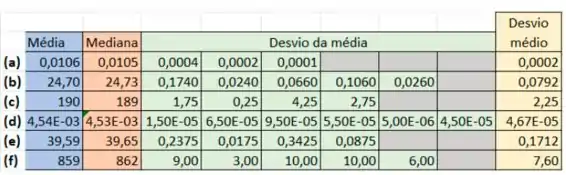
Encontre a média e a mediana para cada um dos conjuntos de dados que seguem. Determine o desvio em relação à média para cada ponto dos conjuntos e encontre o desvio médio para cada conjunto. Use uma planilha eletrônica de cálculo, se desejar.
*(a)
(b)
*(c)
(d)
*(e)
(f)
Passo 1
Fala aí! Como você sugere resolvermos isso aqui? Soma tudo na calculadora e depois divide pra encontrar a média? Pode até ser, mas já que o enunciado deu aquela sugestão de usar uma planilha, é esse caminho que vou escolher.
O software que vou usar aqui é o Excel, mas o processo é o mesmo ou parecido para os demais. O primeiro passo é escrever os números que queremos analisar.
Depois, vamos chamar a função MÉDIA, da seguinte forma:
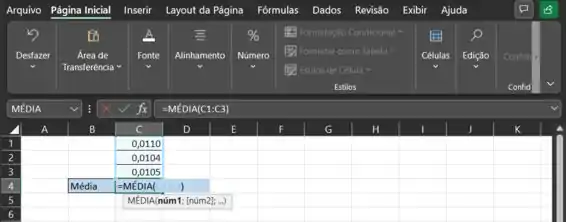
Em uma célula vazia, escrevemos “=MÉDIA(“ e clicamos no primeiro número com o botão esquerdo do mouse e arrastamos até o último, ou podemos também digitar manualmente as posições destes números. Aí é só apertar Enter para obtermos o resultado.
Passo 2
Para encontrar a mediana, usamos a função MED. Procedemos tal como fizemos anteriormente.
Então:
Passo 3
O desvio em relação à média é um pouquinho diferente. Se liga, vou colocar o desvio de cada número ao seu lado.
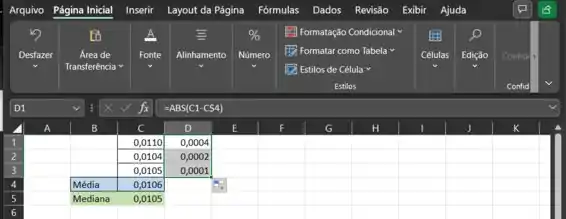
Começando pelo valor 0,0110 ali na célula C1.
Repare que utilizei a função ABS( ) do Excel, ela tem a função de retornar o valor absoluto de uma diferença. Vai ser útil aqui pra gente.
Agora, para não precisar fazer isso manualmente para os outros dados, eu posso simplesmente clicar naquele quadradinho no canto inferior direito da célula que eu preenchi ali e arrastar para baixo. Mas, antes de fazer isso, eu tenho que fixar na fórmula a célula C4, que contém a média. Para fazer isso, eu clico na célula D1 e, ali em cima onde tem a fórmula =ABS(C1-C4) eu insiro um cifrão $ entre o C e o 4. Vai ficar assim:
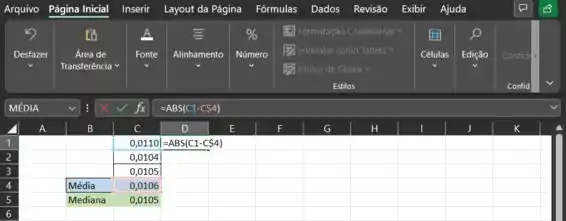
Agora sim, é só arrastar e ver a mágica acontecer.
Passo 4
Pra finalizar, vamos encontrar o desvio médio. O procedimento é igual ao que fizemos no Passo 1. Pra facilitar, podemos simplesmente clicar ali na célula C4 e arrastar para a direita, tal como fizemos no passo anterior.
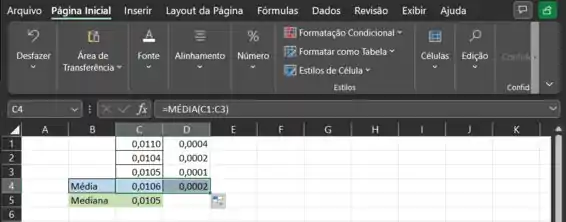
Agora é só repetir estes passos para os demais conjuntos 😉
Resposta
