Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Problemas Numéricos - Ex. 8

A energia do H 2 + com a separação internuclear R é dada pela expressão:

E = E H + e 2 4 π ϵ 0 R - V 1 + V 2 1 + S

Onde EH é a energia de um átomo isolado, V1 é a energia potencial atrativa entre o elétron centrado em um dos núcleos e a carga do outro núcleo, V2 é a atração entre a densidade de superposição e um dos núcleos, e S é a integral de superposição. Os valores são dados a seguir. Faça um gráfico da curva da energia potencial da molécula e determine a energia de dissociação da ligação (em elétrons-volt) e o comprimento da ligação no equilíbrio.

Onde E h = 27,3 e V , a 0 = 52,9   p m e E H = - 1 2 E h

Passo 1

Podemos escrever que E H = E 1 = - h c R H

Desenhando então a tabela a seguir que vamos fazer usando a seguinte equação a 0 R = e 2 4 π ϵ 0 R E h

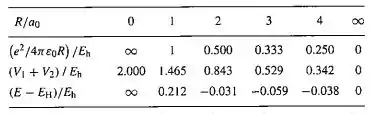
Passo 2

Podemos agora fazer nosso gráfico e determinar quando ocorrerá a menor energia, certo?

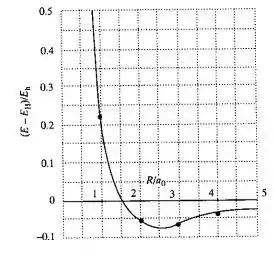
O mínimo ocorre em R = 2,5 a 0 , então R = 130   p m . No comprimento de ligação E - E H = - 0,07 E h = - 1,91 e V

Passo 3

Consequentemente, a energia de dissociação é predita em torno de 1,9 eV e o comprimento de ligação em equilíbrio é em torno de 130 pm.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Entre as moléculas N2, NO, O2, C2, F2 e CN, quais seriam estabilizadas (a) pela adição de um elétron e formação de A B - , (b) pela remoção de um elétron e formação de A B + ?
Disponha as espécies químicas O 2 + , O 2 , O 2 - e O 2 2 - na ordem crescente do comprimento da ligação.
J.G. Dojahn, E.C.M. Chen e W.E. Wentworth caracterizaram as curvas de energia potencial de moléculas diatômicas homonucleares de halogênios e de ânions moleculares do mesmo tipo. Entre as propriedades
Com as expressões dadas no Problema 11.8 e 11.9, mostre que o orbital antiligante é mais antiligante do que o orbital ligante é ligante na maioria das separações internucleares.