Exprima a constante de equilíbrio da reação em fase gasosa em termos do valor do grau de avanço no equilíbrio, , no caso de A e B estarem inicialmente na proporção estequiométrica. Ache a expressão de em função da pressão total, , da mistura reacional e esboce o gráfico dessa função.)

Teremos:

Colocando em evidência:

Temos:

Podemos reescrever como:

Se liga nesse ponto, para não se perder...................

Se a parte de baixo da nossa fração:

Podemos dizer que ela estava dentro da raiz, mas saiu para fora devido ao fato de estar ao quadrado. Então, temos:

Podemos reescrever uma divisão de frações como uma multiplicação, então:

Vamos colocar o em evidência:

Tá, mas qual raiz iremos usar?????????????

Se liga no detalhe, o número de mols não pode ser negativo, então:

E o único jeito disso acontecer é se:

Que pode ser reescrito como:

Olhando na tabela de equilíbrio temos que:

Juntando nossas condições, temos:

Analisando , pela equação precisa ser maior que , primeiro porque se for igual a temos uma divisão por zero o que matematicamente é impossível e segundo se for menor que temos uma raiz quadrada negativa também impossível de ser resolvida.

Com base nisso, teremos o seguinte gráfico:

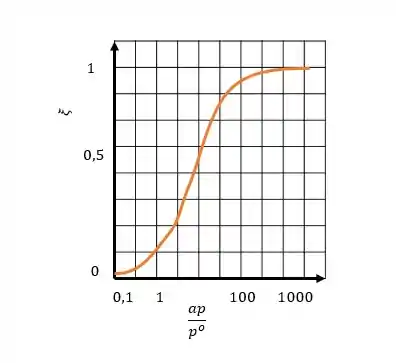
Foi divertido!!!!

Bora matar mais uma!