Enunciado
Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 15.Problemas Numéricos - Ex. 3
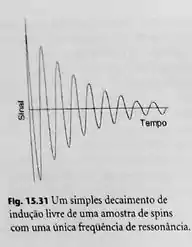
3 – Imagine que a curva FID (decaimento de indução livre) na Fig. 15.31 tenha sido registrada num espectro de 300 MHz e que entre o intervalo entre os máximos das oscilações seja de 0,10 s. Qual a frequência de Larmor dos núcleos e qual o tempo de relaxação spin-spin?
Passo 1
Vamos começar determinando a frequência de Larmor dos núcleos.
A frequência de Larmor, vL, pode ser determinada para este caso onde se tem uma curva de oscilação de FID (decaimento de indução livre) fazendo uma interpretação do comportamento da curva oscilante.
Em uma curva oscilante, o intervalo de tempo entre os pontos de máximos das oscilações da curva, no caso a curva de decaimento, correspondem a diferença de frequência entre ν0 e νL, sendo esta última a frequência de Larmor. Assim,
Assim, a frequência de Larmor é
Passo 2
Agora vamos para o tempo de relaxação spin-spin:
O tempo de relaxação spin-spin representa uma constante de tempo conhecida como o tempo de relaxação transversal, esta constante de tempo está relaciona com a intensidade do sinal pelas seguintes equações:
Onde,
-M é a intensidade no tempo t;
-M0 é a intensidade inicial, em t=0;
-vL é a frequência de Larmor;
-t é o tempo;
-T2 é o tempo de relaxação spin-spin.
Assim, sendo pelas duas equações anteriores temos que quando t = T2, a intensidade M se torna:
Onde, e é a constante de Euler
Assim, o tempo de relaxação spin-spin representa o tempo na qual a intensidade é reduzia a 1/e do valor original da intensidade, M0.
Passo 3
Então, para você determinar esse tempo T2 na qual a intensidade vale 1/e do valor original, você pode utilizar o gráfico da figura 15.31 e localizar em qual ponto de máximo da oscilação representa esse valor de 1/e do valor original, e o tempo será o tempo correspondente a esse ponto máximo, podendo determinar este tempo usando a informação de que os intervalos entre os pontos máximos, valem 0,10 s.
A intensidade em t = T2 como já foi dito vale
Ou seja, o tempo T2 será aquele tempo onde a intensidade é reduzida para cerca de 37% do valor original.
Para te mostrar como poderá ser feito, vou te apresentar o gráfico novamente, agora com mais detalhes, apresentando na curva de oscilação o ponto da intensidade equivalente a cerca de 37% do valor original, de forma aproximada, e o valor do tempo:
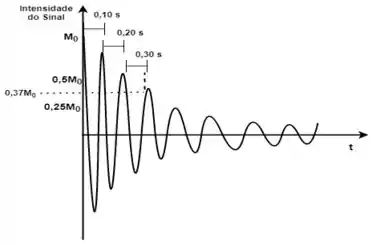
Assim, pela imagem acima da curva de oscilação, pode-se perceber que o tempo de relaxação spin-spin é equivalente a cerca de 0,29s