Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 15.Problemas Numéricos - Ex. 4

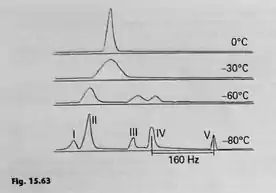
4 – Num estudo clássico de RMN para a medição de barreiras de rotação nas moléculas, P.M. Nair e J.D. Roberts [J. Am. Chem. Soc. 79, 4565(1957)] obtiveram o espectro de RMN, 40 MHz, na molécula do F2BrC-CBrCl2. A Fig. 15.63 reproduz os espectros observados. A 193 K (-80ºC), o espectro exibe cinco picos de ressonância. Os picos I e III, e também os picos IV e V, estão separados por 160 Hz. A razão entre a intensidade integrada do pico II e as intensidades integradas dos picos I, III, IV e V é aproximadamente de 10 para 1. A 273 K, os cinco picos se fundiram num só. Explique o espectro e as modificações com a temperatura. A que velocidade de interconversão as linhas do espectro se fundem numa só? Calcule a energia de ativação da barreira de rotação entre os isômeros rotacionais, admitindo que esteja diretamente relacionada com a velocidade da interconversão dos isômeros.

Passo 1

Vamos primeiro, ver como são as conformações de uma molécula de F2BrC-CBrCl2

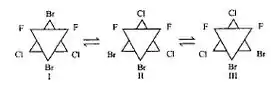
A figura acima apresenta as três conformações rotacionais da molécula de F2BrC-CBrCl2

Vamos explicar o espectro e as variações com a temperatura baseado nessas conformações rotacionais.

Passo 2

Na conformação I os dois átomos de F são equivalentes. Mas nas conformações II e III eles não são equivalentes. A baixa temperatura, o tempo de residência molecular na conformação I é maior do que das conformações II e III, pois nesta conformação há uma menor energia de repulsão para átomos de bromo do que para as conformações II e III. Nas conformações II e III os tempos de residência são iguais.

Já que o tempo de residência da conformação I é maior é esperado que a intensidade do sinal RMN seja mais forte e portanto esteja a única conformação à baixa temperatura.

Nas conformações II e III, os átomos de F, não equivalente, então pode se ocorrer o acoplamento destes a baixa temperatura.

Com o aumento da temperatura, a taxa de rotação entre as conformações II e III aumentam e os dois átomos de flúor se tornam equivalentes nestas conformações.

Passo 3

Sabendo que a velocidade é o inverso do tempo de residência, assim podemos determinar a velocidade de interconversão na qual as linhas se fundem pela seguinte expressão

k = 1 τ

Onde,

-k é velocidade de interconversão;

-τ é o tempo de residência;

Onde, para o tempo de residência, podemos calcula-lo pela seguinte relação

τ = 2 π ∆

Onde, Δ representa a frequência de separação dos picos, assim

∆ = 160   H z

Assim,

k = 1 τ = π ∆ 2 = π ( 1 6 0   s - 1 ) 2

k = 355   s - 1

Passo 4

Como foi dito que a energia de ativação da barreira de rotação entre os isômeros rotacionais está diretamente relacionada com a velocidade da interconversão dos isômeros, então para você calcular a energia de ativação, você pode usar a expressão de Arrhenius que é a seguinte

k = A exp ⁡ - E a R T

Onde,

-k é a velocidade de interconversão;

-A é uma constante intrínseca ao processo reacional;

-Ea é a energia de ativação;

-R é a constante dos gases ideais, R=8,314 J mol-1 K-1;

-T é a temperatura.

A velocidade de interconversão ocorre a -30ºC=243 K e assumindo que em uma temperatura de -60ºC=213 K a velocidade de interconversão seja 1/3 do valor da velocidade de interconversão a -30ºC, assim

A T=243 K

k = 355   s - 2

A T’=213 K

k ' = k 3 = 355   s - 1 3 = 118 , 33   s - 1

Passo 5

Para determinarmos a energia de ativação para o processo em questão, vamos atribuir as expressões de Arrhenius para as duas temperaturas:

Para T=243K

k = A exp ⁡ - E a R T

Para T’=213K

k ' = A exp ⁡ - E a R T '

Vamos dividir as duas expressões:

k ' k = A exp ⁡ - E a R T ' A exp ⁡ - E a R T = exp ⁡ - E a R T ' exp ⁡ - E a R T

Pela propriedade de exponencial:

exp ⁡ - E a R T ' exp ⁡ - E a R T = exp ⁡ - E a R T ' - - E a R T = exp ⁡ E a R T - E a R T '

Assim,

k ' k = exp ⁡ E a R 1 T - 1 T '

Passo 6

Aplicando Ln em ambos os lados da equação acima

ln ⁡ k ' k = ln ⁡ exp ⁡ E a R 1 T - 1 T '

ln ⁡ k ' k = E a R 1 T - 1 T '

Isolando Ea

E a = R ln ⁡ k ' k 1 T - 1 T ' - 1

Calculando a energia de ativação:

E a = ( 8,314   J   m o l - 1 K - 1 ) ln ⁡ 1 3 1 243 - 1 213 - 1 K

E a = 16000   J   m o l - 1 = 16   k J   m o l - 1

Resposta

k = 355   s - 1

E a = 16000   J   m o l - 1 = 16   k J   m o l - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Entre as transições seguintes, quais as permitidas no espectro de emissão normal de um átomo? (a) 5 d → 2 s , (b) 5 p → 3 s , (c) 5 p → 3 f .
O hidrogênio é o material mais abundante em todas as estrelas. Entretanto, as linhas de absorção ou de emissão devidas ao hidrogênio são de muita pouca intensidade nos espectros de estrelas com temper
23a – Dê as estruturas hiperfinas dos radicais XH2 e XD2, sendo X um núcleo com I=5/2.
22b – O espectro de EPR de um radical com dois núcleos equivalentes de um certo nuclídeo é desdobrado em cinco linhas cujas intensidades estão na razão 1:2:3:2:1. Qual o spin dos núcleos?
21b – O radical naftaleno aniônico tem g=2,0024. Em que campo deve haver ressonância num espectrômetro de EPR que opera a (a) 9,312 GHz e (b) 33,88 GHz?