Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 16.1 - Ex. 54
Quando o íon paramagnético é oxidado para , o íon se torna diamagnético. No entanto, quando o íon paramagnético é reduzido para , o íon permanece paramagnético. Explique essas observações.
Passo 1
Bora pra outra?
Antes de qualquer coisa vamos conceituar isto ai de dia e paramagnético, ok?
Uma substância com elétrons não emparelhados é dita paramagnética e é puxada para um campo magnético. Enquanto que uma substância sem elétrons desemparelhados é diamagnética e é empurrada para fora de um campo magnético.
No primeiro caso nós temos se oxidando para , o ânion será sempre , não é mesmo ?
Mas e quanto ao NOX do cobalto? Vamos olhar!
No primeiro caso,
Agora vamos distribuir estes elétrons:
[Co2+] =[Ar] 3d7
E para
Distribuindo estes elétrons:
[Co3+] =[Ar] 3d6
Como temos seis ligantes monodentados teremos número de coordenação igual a seis e geometria octaédrica.
Se sabemos a geometria também sabemos qual diagrama usar, não é assim?
Agora, olhando para os ligantes, podemos perceber que eles são de campo forte e, por isso, seus elétrons serão distribuídos primeiramente nos orbitais menos energéticos.
Para distribuímos sete elétrons:
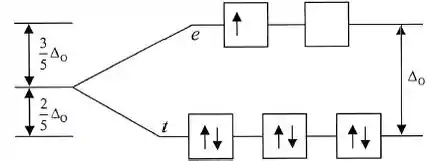
Temos aqui um elétron desemparelhado, ou seja, paramagnético.
Para distribuímos seis elétrons:
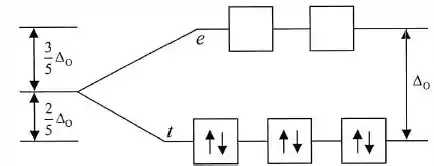
Nenhum elétron desemparelhado, não é? Molécula diamagnética então.
Faremos a mesma distribuição para os outros compostos.
Passo 2
Neste caso temos se oxidando para , aqui novamente mantemos o ânion constante, sempre , não é mesmo ?
Igual ao caso anterior, para temos o cobalto II:
[Co2+] = [Ar] 3d7
E para
[Co3+] =[Ar] 3d6
Como são três ligantes bidentados teremos número de coordenação igual a seis e geometria octaédrica.
Agora, olhando para os ligantes, podemos perceber que eles são de campo fraco e, por isso, seus elétrons serão distribuídos primeiramente nos orbitais vazios.
Para distribuímos sete elétrons:
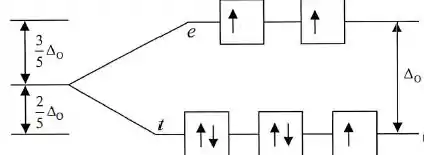
Temos aqui três elétrons desemparelhados, ou seja, paramagnético.
Para distribuímos seis elétrons:
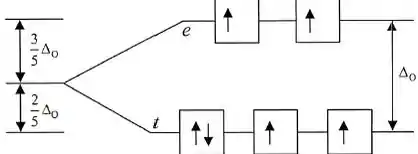
Ainda quatro elétrons desemparelhados, não é? Molécula ainda paramagnética.
A grande questão aqui foi o ligante, concordam? O fato dele ser forte permitiu com que a molécula se transformasse em diamagnética. Entretanto, quando o ligante é fraco os elétrons se encontram majoritariamente desemparelhados, dificultando esta mudança.
Tranquilinha?