Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 8.1 - Ex. 96
As populações dos estados de spin para cima e para baixo em um campo magnético B são dadas:
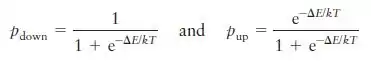
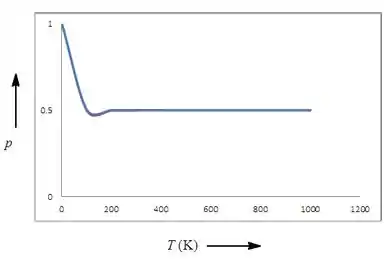
Em que é a diferença de energia entre os dois estados de spin (consulte o Exercício 8.95). Lance essas duas populações em função da temperatura para . (Ver Quadro 8.1.)
Passo 1
Essa é trabalhosa galera, então vamos com calma!
De acordo com o exercício anterior:
Então:
Para
Substituindo nas fórmulas:
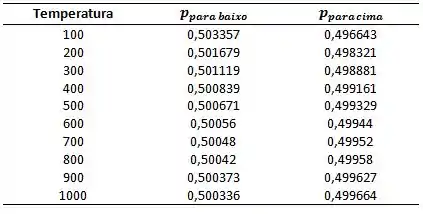
Olhando os valores de entropia com a temperatura de 100 – 1000 K:
Passo 2
Colocando ambas no gráfico:
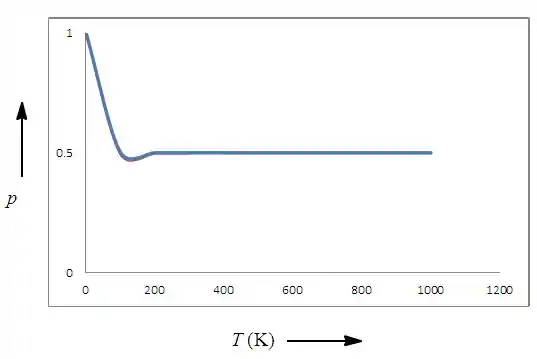
Tranquilinha?!
Resposta
Exercícios de Livros Relacionados
8.2 Um aquecedor elétrico produz 2,3 kW (1 W = 1 J/s). (a) Em que velocidade ele gera entropia em uma sala que está em 24°C? (b) Quanto de entropia ele gera por dia? (c) A entropia gerada seria maior
77. Imaginando a desordem estatística, você esperaria que um cristal da molécula octaédrica cis-MX2H4 tivesse entropia residual igual, maior ou menor do que isômero trans? Explique sua conclusão.
92. De acordo com as teorias atuais da evolução biológica, os aminoácidos e os ácidos nucleicos foram produzidos a partir de reações de ocorrecia aleatória, que envolviam compostos que, imagina-se, es
78. Existem três benzenos substituídos diferentes com formula C6H4F2.(a) Desenhe as estruturas dos três compostos.(b) Suponha que os anéis de benzeno tem empacotamento semelhante nas três redes crista
90. O ácido acético, CH3COOH(l), pode ser produzido a partir (a) da reação do metanol com monóxido de carbono;(b) da oxidação do etanol;(c) da reação do dióxido de carbono com metano. Escreva equações