Casos especiais do critério de Routh-Hurwitz
Produzido por Alexandre NunesTeoria
Introdução
Bom agora que você já consegue utilizar o critério de Routh-Hurwitz com um pé nas costas e os olhos vendados, você deve estar achando que já está preparado para tudo, que já pode sair por aí determinando estabilidade de qualquer sistema a torto e a direito e que tudo na vida são flores. Spoiler: não são.
Existem alguns casos bem específicos que vão deixar a gente numa sinuca de bico. Você vai olhar para eles e ficar assim:

Mas calma jovem, estou aqui para te ajudar.
São dois casos basicamente que vão ser uma pedra no nosso sapato: quando tivermos um zero na primeira coluna do diagrama de Routh-Hurwitz e quando tivermos uma linha inteira composta de zeros no diagrama.
Nesse tópico vamos aprender estratégias para contornar essas situações e poder determinar a estabilidade do sistema mesmo assim. Sigam-me os bons!
Um zero na primeira coluna – Método do épsilon
Um zero na primeira coluna sempre será algo que vai atrapalhar demais quando estivermos aplicando o critério de Routh-Hurwitz. Isso acontece porque os coeficientes da primeira coluna sempre são os denominadores na hora de determinar os coeficientes da linha debaixo. Se tivermos um zero na primeira coluna, na linha seguinte teremos uma divisão por zero, e nós queremos fugir de divisões por zero.
Então olha só, considere a seguinte função de transferência de uma mala fechada:
A equação característica será:
Vamos aplicar o critério de Routh-Hurwitz normalmente como aprendemos na seção anterior. Primeiramente devemos completar as duas primeiras com os coeficientes da equação característica:

Por enquanto tudo certo, nada fora do normal. Seguindo com os cálculos para a próxima linha usando as correlações que vimos no último tópico:
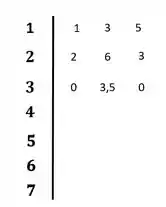
Opa, apareceu um zero ali na primeira coluna, mas vamos continuar para ver o que aconteceria.
Para calcular o primeiro coeficiente da linha , deveríamos fazer:
Como havia dito, quando temos um zero na primeira coluna, na linha seguinte em que esse zero aparece teremos uma divisão por zero. E é aqui que a gente fica encurralado sem saber para onde correr.
Como eu disse, nem tudo na vida são flores, mas também, nem tudo são espinhos. Ainda bem que algum consagrado inventou o método do épsilon.
Esse método consiste em substituir o zero na primeira coluna por um épsilon () e calcular todos os valores seguintes do diagrama em função desse épsilon.
Sendo assim:

Por fim, o que devemos fazer é considerar dois cenários: caso épsilon seja um número pequeno positivo, e caso épsilon seja um número pequeno negativo, e avaliar para cada um dos casos quais seriam os sinais dos coeficientes da primeira coluna. Então vamos lá:
Caso épsilon seja um número muito pequeno positivo o primeiro coeficiente da linha 4 seria negativo, e o primeiro coeficiente da linha 5 seria positivo. Sendo assim, haveria mudança de sinal da linha para a linha , e da linha para a linha .
Caso épsilon seja um número muito pequeno negativo. O primeiro coeficiente da linha seria negativo e o primeiro coeficiente da linha e da linha seriam positivos. Sendo assim, ocorreriam mudanças de sinal da linha para a linha e da linha para a linha .

Portanto, o sistema é instável. Para que ele fosse estável ele não poderia apresentar nenhuma mudança de sinal em ambos os casos.
Uma linha composta de zeros
Um outro caso que pode aparecer também para nos atazanar é quando temos uma linha inteira composta por zeros. Vamos ver um exemplo com a seguinte função de transferência para uma malha fechada.
A equação característica é então:
Colocando no diagrama de Routh-Hurwitz:
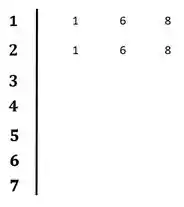
Calculando a próxima linha:
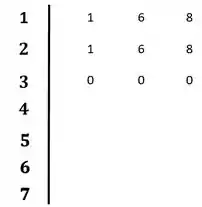
E agora, como sairemos dessa enrascada? É fácil, olha só.
É importante ressaltar que sempre que tivermos duas linhas iguais, como no exemplo, cairemos nesse caso de ter uma linha de zeros, mas nem sempre que tivermos uma linha de zeros, as duas primeiras linhas serão iguais.
Quando isso acontecer nós invocaremos um polinômio auxiliar. O polinômio auxiliar será obtido através da linha anterior à linha de zeros, nesse caso, a linha será a linha .
Cada linha do diagrama de Routh-Hurwitz tem uma potência. A primeira linha tem potência igual à ordem do polinômio da equação característica, para esse caso será , a segunda linha uma ordem a menos e assim por diante.
Para determinar nosso polinômio auxiliar, nós vamos olhar para a ordem da linha acima, como a linha acima é a segunda linha, o polinômio terá ordem . Os coeficientes desse polinômio serão os coeficientes da linha acima, e sempre pularemos uma potência, ou seja, vamos começar na potência de 4, seguir para a de 2 e terminar na 0. Sendo assim, o nosso polinômio auxiliar será:
Repare que começamos com porque a segunda linha tem ordem . Fomos pulando as potências e os coeficientes do polinômio são os coeficientes da segunda linha do diagrama.
Agora devemos derivar o nosso polinômio em relação a :
Os coeficientes desse novo polinômio serão os coeficientes que substituiremos na linha de zeros:
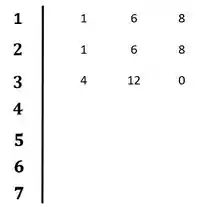
Agora é só continuar resolvendo normalmente:
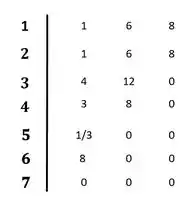
Não existe mudança de sinal entre os coeficientes da primeira coluna, o que indica que o sistema é estável.
Uma propriedade bacana é que a presença de uma linha de zeros indica que existem raízes da equação característica que são simétricas com relação à origem. O número de raízes simétricas é igual ao grau do polinômio auxiliar.
É legal perceber que depois da aparição da linha de zeros (e da determinação do polinômio auxiliar) as trocas de sinais são referentes às raízes simétricas. Ou seja, se depois da aparição da linha de zeros, não acontecer troca de sinais, significa que não existe nenhuma raiz simétrica no semiplano direito, dessa forma, a única forma das raízes serem simétricas com relação à origem é se elas estiverem sobre o eixo imaginário . Vamos explorar essa propriedade melhor nos exercícios.