Estabilidade e critério de Routh-Hurwitz
Produzido por Alexandre NunesTeoria
Introdução
Agora que nós já vimos um pouco melhor os diferentes tipos de função de transferência que nós podemos encontrar no nosso caminho, é hora de expandir um pouco nossos horizontes e olhar o nosso sistema de controle de uma forma mais ampla.
Às vezes podemos dar de cara com um cara desse tipo aqui:
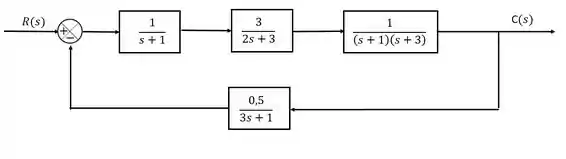
Essa malha de controle vai ter função de transferência do tipo;
E aí a gente vai esbarrar em um problema muito comum no controle de processos: essa malha é estável ou instável?
Em alguns casos, a nossa malha de controle pode ser instável, isso quer dizer que conforme o tempo passa, a resposta do processo ao invés de se aproximar de um valor determinado, vai se afastando cada vez mais desse valor. Quando isso acontece, nós falamos que o sistema é instável.
Bora aprender como a gente vê se a nossa malha é estável ou instável?
Controle feedback
Antes de a gente se aprofundar nos critérios de estabilidade, vamos dar uma relembrada em controle feedback.
O controle feedback é o mais clássico dos controles, é aquele que você tem que sacar tudo!
Nele, nós vamos ter duas variáveis principais: a variável controlada, e a variável manipulada. Basicamente a variável controlada é aquela que nós queremos manter em um determinado setpoint, enquanto a variável manipulada é a variável que nós vamos mexer para manter a variável controlada no nosso setpoint.
O diagrama de blocos simplificado do controle feedback é assim:
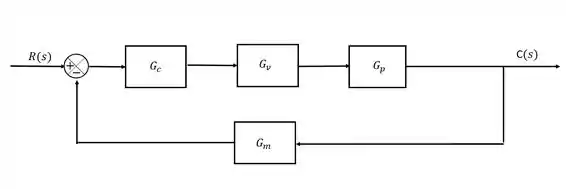
Vamos entender o que está acontecendo!
, , e são as funções de transferência do controlador, da válvula, do processo e do sensor-transmissor, respectivamente.
Presta atenção agora: após o nosso processo acontecer (em ) nós temos um valor para a nossa variável controlada , esse valor será medido por um sensor transmissor () e comparado com um valor de setpoint (), após fazer essa comparação o controlador vai interpretar essa diferença entre variável medida e setpoint e tomar uma decisão. Quando ele toma essa decisão, ele envia um sinal para a válvula () que altera a variável manipulada, fazendo que aconteça uma mudança no processo que altera o valor da variável controlada. E tudo isso acontece novamente. Incrível né?
Para o controle feedback tradicional, a função de transferência da malha fica:
Caso você não tenha entendido como chegamos a essa expressão, dá uma revisadinha na aula de álgebra de diagrama de blocos, você vai ver que não tem mistério.
Equação característica
Agora que já demos uma revisada em controle feedback, vamos começar a falar de fato de estabilidade.
Sempre que formos avaliar a estabilidade de um sistema, devemos olhar para a sua equação característica.
“AH MAS O QUE DIABOS É EQUAÇÃO CARACTERÍSTICA? ”
Calma, não precisa gritar, já te explico.
Equação característica, nada mais é do que a expressão que fica no denominador da nossa função de transferência. Então, quando a gente estiver trabalhando com controle feedback, nossa equação característica vai ser:
Para o exemplo que nós demos lá no início, ficaria assim:
Rearranjando:
Na maioria dos casos a equação característica será um polinômio de ordem . Nesse caso é um polinômio de ordem .
Esse polinômio vai conter os segredos que vai nos dizer se o nosso sistema é estável ou instável.
O primeiro critério que a gente vai poder observar logo de cara é o critério dos sinais dos coeficientes.
O critério dos coeficientes diz que uma malha só é estável se todos os coeficientes da função de transferência tiverem o mesmo sinal.
Mas fique atento, esse critério é necessário, porém não é suficiente. Isso quer dizer que se o critério não for atendido, a malha necessariamente será instável, porém, se ele for atendido, não é possível determinar nada sobre a estabilidade do sistema.
Para garantir a estabilidade de um processo então, é necessário que todas as raízes da equação característica sejam números reais negativos ou números imaginários com a parte real negativa.
Em equações de até terceira ordem, talvez seja fácil determinar essas raízes, entretanto, em equações de ordem superior a coisa complica um pouco, e por isso precisamos de ferramentas para determinar de maneira mais fácil se o sistema é estável ou não.
Critério de Routh-Hurwitz
Uma ferramenta que temos para determinar a estabilidade de uma malha é o critério de Routh-Hurwitz.
Com esse critério, nós construiremos um diagrama, e esse diagrama será o que nos dirá se o sistema é estável ou instável.
Bora colocar a mão na massa então.
Imagina que a gente tenha uma equação característica de quinta ordem:
Então, para construir nosso digrama nós colocaremos nossos coeficientes na matriz da seguinte forma:
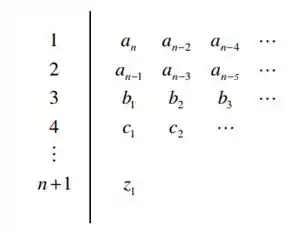
Isso quer dizer que os coeficientes das duas primeiras linhas serão preenchidos pelos coeficientes da equação característica. Para o exemplo da equação de quinta ordem:
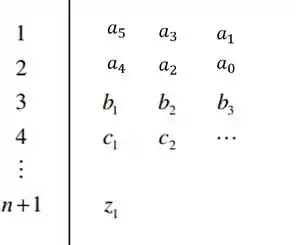
Após preencher as duas primeiras linhas com coeficientes da equação característica, devemos calcular os outros termos do diagrama até a linha . Esses termos podem ser calculados da seguinte forma:
Para a linha :
E assim sucessivamente.
Para a linha 4:
E assim sucessivamente em todas as linhas até todos os termos serem .
Após montar todo o diagrama, o critério de Routh-Hurwitz diz que o sistema é estável se todos os coeficientes da primeira coluna forem positivos.
Cada mudança de sinal na primeira coluna, indica uma raiz da equação característica no semiplano direito (parte real positiva) e isso torna o sistema instável
Juro que na prática é mais fácil do que parece, bora praticar?
Controle feedback
Equação característica
Critério de Routh-Hurwitz
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Defina a estabilidade do sistema representado pela malha feedback abaixo:
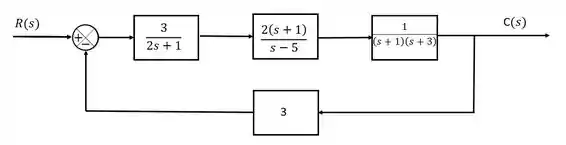
Passo 1
O primeiro passo, sempre que queremos determinar a estabilidade de uma malha, é encontrar a equação característica da malha. Para esse sistema, como estamos trabalhando com um feedback clássicozão, a função de transferência ficará assim:
Caso você tenha dúvidas em como obter essa expressão, dá uma revisadinha na aula de álgebra de diagrama de blocos.
Nós precisamos da equação característica, e ela sempre será o denominador da função de transferência. Então:
Passo 2
Vamos então deixar essa equação mais bonitinha pra gente poder pensar melhor sobre a estabilidade. Multiplicando toda a equação pelo denominador:
Fazendo as multiplicações:
Passo 3
Agora que já temos a nossa equação característica, poderíamos determinar a estabilidade dela pelo critério de Routh-Hurwitz. Entretanto, só de olhar pra carinha dela, já conseguimos ter um spoiler da nossa resposta.
O critério dos coeficientes diz que para o sistema ser estável, a sua equação característica precisa ter todos os sinais iguais.
Nesse caso, o critério não foi atendido. Portanto o sistema é instável.
Obs: só lembrando que esse critério é necessário, porém não suficiente.
Resposta
O sistema é instável de acordo com o critério dos coeficientes.
Exercício Resolvido #2
Elaboração própria
Pelo critério de Routh-Hurwitz, determine se o sistema cuja função de transferência está representada abaixo é estável:
Passo 1
A questão é bem direta: precisamos definir a estabilidade do sistema.
A nossa equação característica será:
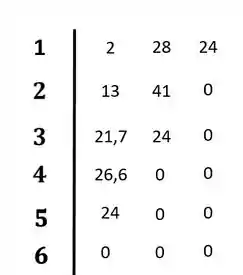
E precisamos aplicá-la no diagram de Roth-Hurwitz abaixo:
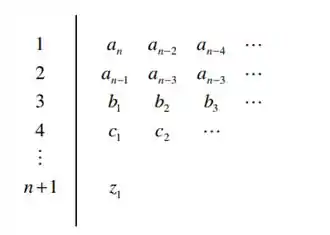
Passo 2
O primeiro passo seria então, distribuir os coeficientes nas duas primeiras linhas:
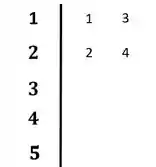
E então, podemos começr a calcular os outros termos.
Para a terceira linha:
Colocando no diagrama:
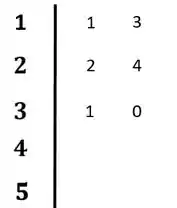
Passo 3
Calculando agora as linhas 4 e 5:
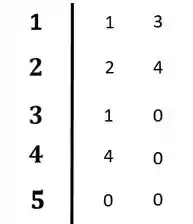
Colocando tudo no diagrama:
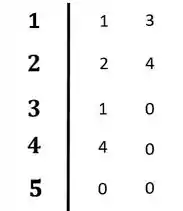
Resposta
O sistema é estável. Não ocorreu mudança de sinal na primeira coluna do diagarama.
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 6.1
Construa o diagrama de Routh para o sistema mostrado abaixo:
Passo 1
Como já temos a função de transferência da malha, nossa função é simplesmente:
Devemos então calcular o diagrama de Routh do sistema, seguindo o modelo:
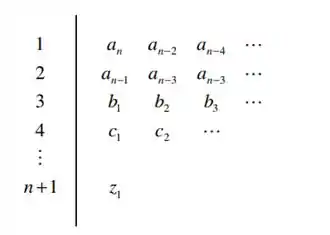
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
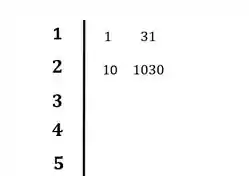
Passo 3
Em seguida, iremos calcular os valores dos coeficientes da segunda linha:
Colocando os valores no diagrama:
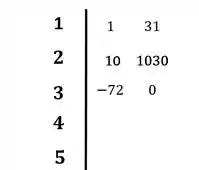
Para a linha 4:
E para a linha 5:
Colocando tudo no diagrama:

Resposta

Exercício Resolvido #4
Elaboração própria
Determine se o sistema representado pela função de transferência abaixo é estável:
Passo 1
A nossa equação característica é:
E devemos montar nosso diagrama de Routh, seguindo o modelo para equação com 5 termos:
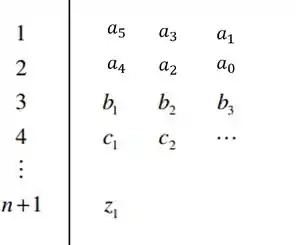
Passo 2
Primeiramente, vamos colocar os coeficientes da equação característica nas duas primeiras linhas:
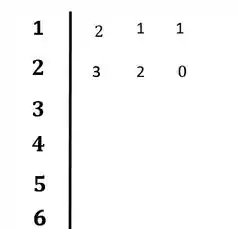
Passo 3
Vamos então calcular os faores da linha 3:
Colocando no diagrama:
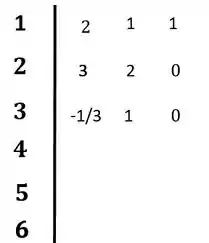
Passo 4
Calculando os fatores da quarta linha:
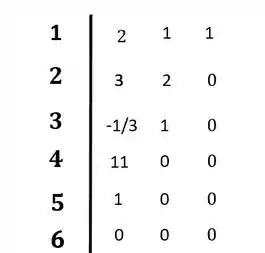
E os termos da quinta e sexta linha:
Colocando no diagrama:
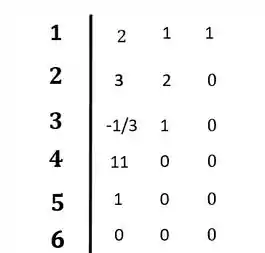
O sistema não é estável pois ocorreu mudança de sinal na primeira coluna do diagrama de Routh-Hurwitz.
Resposta
Sistema instável.
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 6.2
Determine a estabilidade da função de transferência em malha fechada:
Passo 1
O primeiro passo será determinar a nossa equação característica, como a função de transferência dada já é a da malha, a equação característica é:
Em seguida devemos utilizar o diagrama e Routh-Hurwitz para determinar a estabilidade do sistema:

Passo 2
Vamos então dispor os coeficientes da equação característica nas duas primeiras linhas do diagrama de Routh-Hurwitz:

Passo 3
Em seguida, calculamos os coeficientes da linha 3:
Substtituindo os valores encontrados no diagrama:

Passo 4
Seguindo os cálculos agora, vamos para a linha 4:
Não precisamos calcular os próximos termos dessa linha, pois eles serão .
Colocando no diagrama:

Passo 5
Calculando as últimas linhas agora:
No diagrama:
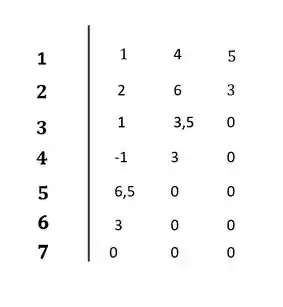
Sendo assim, o sistema é instável, pois apresenta duas mudanças de sinal na primeira coluna do diagrama, indicando a presença de duas raízes no semi-plano direito (parte real positiva).
Resposta
Sistema instável.
Exercício Resolvido #6
Elaboração própria
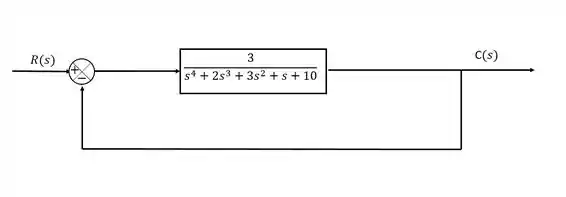
Determine se a malha abaixo é estável:
Passo 1
Primeiramente devemos definir nossa equação característica. Para isso, precisamos da função de transferência da malha:
Com sendo a função de transferência do bloco.
A nossa equação característica será então:
Rearranjando:
Agora que já temos nossa equação característica, precisamos aplicá-la no modelo abaixo para conseguir determinar a estabilidade da malha:
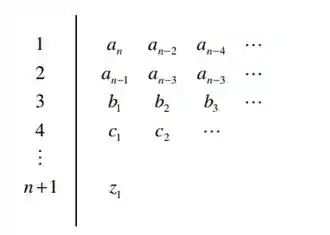
Passo 2
Vamos então, dispor os coeficientes da equação característica nas duas primeiras linhas:
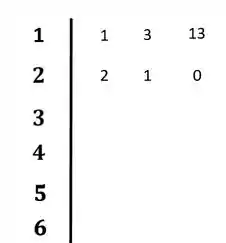
Vamos calcular agora os elementos da linha 3:
Colocando no diagram:
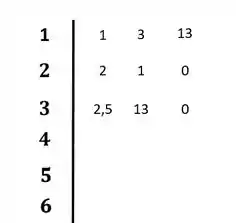
Passo 3
Calculando agora os elementos da terceira linha:
Passando para o diagrama:
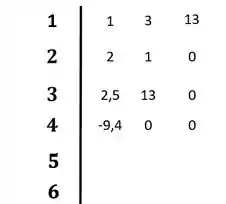
Passo 4
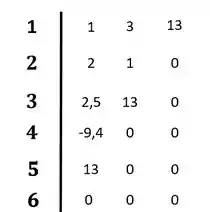
Agora para as duas últimas linhas:
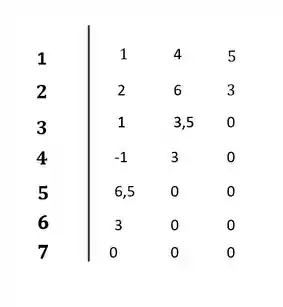
Completando o diagrama:
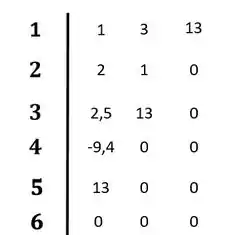
Resposta
O sistema é instável pois ocorre mudança de sinais na primeira coluna do diagrama de Routh-Hurwitz.
Exercício Resolvido #7
Elaboração própria
Determine se o sistema abaixo é estável: 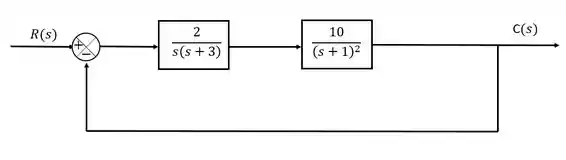
Passo 1
Primeiro precisamos definir nossa equação característica. Já vimos que para o feedback unitário, a equação característica fica da seguinte forma:
Onde e são os blocos do diagarama. Então:
Rearranjando:
Com a nossa equação característica em mãos, só precisamos aplicar o critério de Routh-Hurwitz para definir a estabilidade:
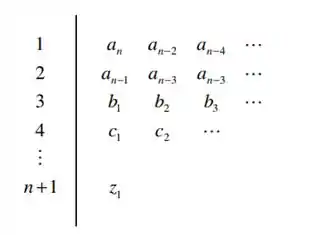
Passo 2
Vamos substituir os termos no diagrama então:
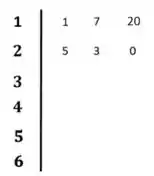
E vamos calcular os termos da terceira linha conforme as fórmulas:
Vamos colocar esses termos no diagrama:
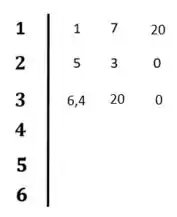
Passo 3
Vamos passar então para a quarta linha:
Então:

Passo 4
Para finalizar. Calculamos os coeficientes das duas últimas linhas:
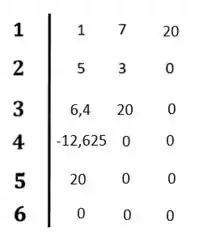
Completando nosso diagrama:
Resposta
O sistema é instável porque existe mudança de sinal na primeira coluna do diagrama de Routh-Hurwitz.
Exercício Resolvido #8
Elaboração própria
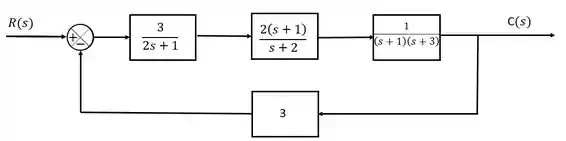
Caracterize a malha abaixo quanto à sua estabilidade:
Passo 1
Primeiramente, vamos definir a função de transferência equivalente da malha, para que possamos encontrar a nossa equação característica.
Como esse é aquele diagrama feedback mais comum, a função de transferência será:
Caso você tenha dúvidas em como obter essa expressão, dá uma revisadinha na aula de álgebra de diagrama de blocos.
Como a equação característica é sempre o denominador da função de transferência, nossa equação característica será:
Vamos então rearranjar essa equação para conseguir usar o critério de Routh-Hurwitz. Multiplicando toda a equação pelo denominador:
Fazendo as multiplicações:
Por fim, devemos substituir os termos no diagrama de Routh-Hurwitz, conforme o modelo:
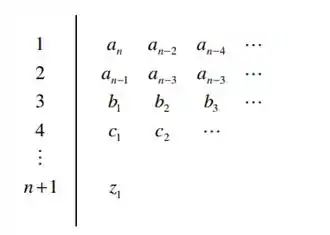
Passo 2
Substituindo os termos nas duas primeiras linhas:
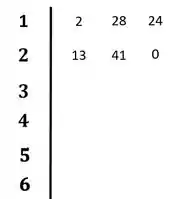
E vamos calcular os termos da terceira linha conforme as fórmulas:
Colocando esses resultados no diagrama:

Passo 3
Vamos passar então para a quarta linha:
Então:
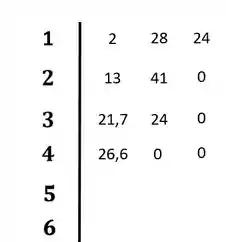
Passo 4
Para finalizar. Calculamos os coeficientes das duas últimas linhas:
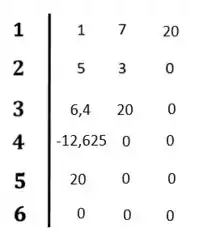
Completando nosso diagrama:
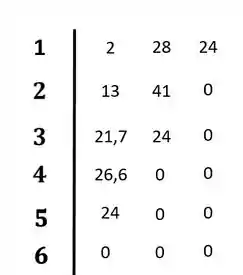
Resposta
O sistema é estável porque não existe mudança de sinal na primeira coluna do diagrama de Routh-Hurwitz.