Erro em regime permanente e sensibilidade à perturbação
Teoria
Introdução
O erro no regime permanente é um dos principais fatores que caracterizam o quão bom um sistema de controle é. Por isso é muito importante saber determinar esse erro e conhecer todas as implicações e tudo que envolve esse tópico tão importante no estudo de controle.
O erro em regime permanente, é a diferença entre entrada e saída quando . Esse erro pode ser , pode ser um constante, ou pode ser infinito. Veremos daqui a pouco como calcularemos isso.
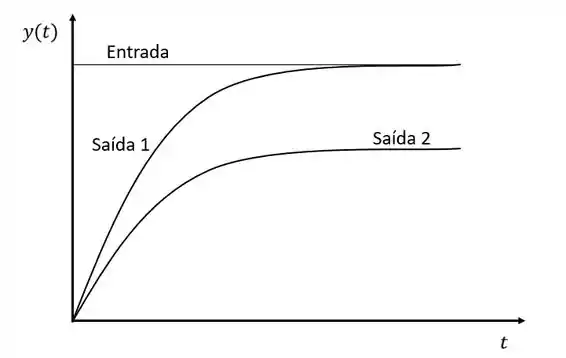
Na figura acima, o gráfico representa três curvas: uma entrada degrau, e duas respostas de saída à essa mesma entrada.
Podemos perceber que a quando , a saída 1 tende ao mesmo valor do degrau da entrada, enquanto que a saída 2 fica constante em um valor abaixo do valor da entrada. Sendo assim dizemos que:
Ok, mas como a gente calcula esse erro? E como eu sei quando o erro é , quando não é e quando é infinito? Bora descobrir?
Tipos de função de transferência
Antes da gente pular de cabeça no tema dos erros, vamos abrir um parênteses aqui rapidinho para a gente definir algumas coisas bem rápidas.
Uma coisa que pode nos ajuda muito a saber que tipo de erro nosso sistema vai ter, é saber o tipo de função de transferência do nosso processo quanto à quantidade de polos na origem, isto é, a quantidade de termos no denominador.
- Uma função de transferência é do tipo 0, quando não tem nenhum polo na origem.
- Uma função de transferência é do tipo 1, quando tem um polo na origem:
- Uma função de transferência é do tipo 2, quando tem dois polos na origem:
- É preciso que exista pelo menos uma função do tipo 1 ou superior, à esquerda da perturbação, se ela for do tipo degrau;
- É preciso que exista pelo menos uma função do tipo 2 ou superior, à esquerda da perturbação, se ela for do tipo rampa;
- É preciso que exista pelo menos uma função do tipo 3 ou superior, à esquerda da perturbação, se ela for do tipo parábola.
E assim, sucessivamente. Mole, né?
Erro em regime permanente
Beleza, agora vamos começar a calcular nossos erros de fato. Considere o seguinte diagrama de blocos:
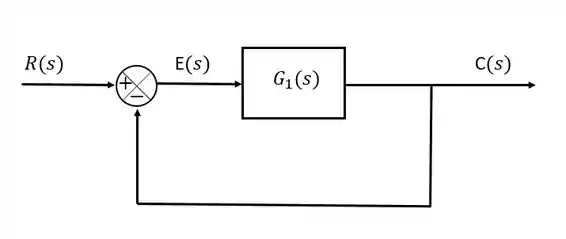
Esse diagrama de blocos é chamado de feedback (ou retroalimentação) unitário. Isso porque a linha de retroalimentação não tem nenhum bloco.
Para calcular nosso erro , vamos nos utilizar das equações que podemos tirar do diagrama de blocos:
Além disso:
Substituindo a de baixo na de cima:
Essa é a expressão do erro para uma malha de feedback unitário. Como nós queremos encontrar o erro do estado estacionário, devemos usar o teorema do valor final.
Para usar o teorema do valor final, basta multiplicar a expressão por e fazer o limite de :
Erros para diferentes tipos de sistema
Como vimos, para um sistema de feedback unitário, o erro pode ser calculado como:
Vamos supor que seja uma entrada degrau:
Ou seja, caso seja o erro do sistema será , caso contrário, o sistema carregará um erro no estado estacionário.
Repare que só será se ele tiver pelo menos um polo na origem. Então, podemos concluir que para a entrada degrau, o erro será uma constante se a função for do tipo 0, e será 0 se a função for do tipo 1 ou superior.
Agora, imaginemos que a entrada seja do tipo rampa:
Portanto, o erro no estado estacionário será , se for , para que isso aconteça, a função tem que ser pelo menos do tipo 2. Se ela for do tipo 1 o erro será uma constante, e se ela for do tipo 0 o erro será infinito.
De maneira geral:
Para uma entrada degrau (), o erro será uma constante caso seja do tipo 0, e será , caso seja do tipo 1 ou superior;
Para uma entrada rampa (), o erro será infinito caso seja do tipo 0, será uma constante com do tipo 1, e será 0 se for do tipo 2 ou superior;
Para uma entrada do tipo parábola (), o erro será infinito caso seja do tipo 1 ou 0, será uma constante com do tipo 2, e será 0 se for do tipo 3 ou superior;
E assim o padrão se repete para entradas de ordem superior.
Erro causado por perturbações
Além da entrada, também podemos calcular nosso erro para uma perturbação, olha só:
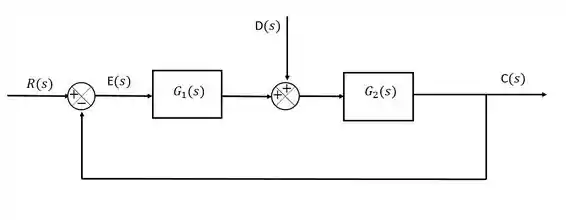
Nós temos que:
Substituindo a segunda na primeira e resolvendo para :
Esse erro pode ser dividido em duas parcelas:
Onde é o erro referente à entrada que nós já vimos, e é o erro referente ao distúrbio:
Para encontrar o erro do estado estacionário causado pelo distúrbio:
Se assumirmos que é uma perturbação degrau, teremos:
Dividindo o numerador e o denominador por :
Podemos perceber que o erro causado pelo distúrbio aumenta com o aumento de e com a diminuição de .
Rejeição à perturbação
Para nós, sempre será interessante que o erro causado por distúrbios seja no estado estacionário. Entretanto, nem sempre isso será possível.
Vamos continuar analisando nosso exemplo anterior.
A equação para o erro causado por uma perturbação degrau unitário pode ser descrita como:
Como concluímos há pouco, quanto maior for o limite para de menor será o erro no estado estacionário, portanto, quando tende a infinito, o erro tende a , então dizemos que o sistema rejeita assintoticamente a perturbação. Para que isso aconteça, a função precisa ser pelo menos do tipo 1.
Repare que se a função for do tipo 1 ou superior, nada poderá ser concluído sobre o erro. Repare também que a função se encontra após a introdução do distúrbio na malha (à direita), enquanto a função se encontra antes da introdução do distúrbio (à esquerda).
A conclusão que tiramos disso é que para um sistema rejeitar assintoticamente uma perturbação do tipo degrau, ele precisa ter pelo menos uma função do tipo 1 ou superior à esquerda da introdução da perturbação.
Caso o distúrbio for do tipo rampa, o erro em estado estacionário poderá ser calculado assim:
Portanto, para que o , a função precisa ser do tipo 2 ou superior, já para a função , não existe nenhuma conclusão que se possa chegar.
É possível então perceber uma tendência. Para o sistema rejeitar assintoticamente uma perturbação:
Tipos de função de transferência
Erro em regime permanente
Erros para diferentes tipos de sistema
Erro causado por perturbações
Rejeição à perturbação
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 7.1. Adaptado
Determine o erro em regime permanente para o sistema da figura abaixo. Sabendo que:
E que é um degrau unitário.
Passo 1
Pelo diagrama temos que:
E:
Substituindo a primeira na segunda:
Portanto:
Passo 2
Substituindo o valor de que foi dado no enunciado e a entrada degrau, encontraremos a expressão do erro do sistema:
Rearranjando:
Passo 3
Para calcular o erro no estado estacionário, devemos aplicar o teorema do valor final na expressão do erro do sistema:
Cortando o :
Resposta
Exercício Resolvido #2
Professor Lizandro Sousa, UFF, Lista 5 – 2019.2. Exercício 3. Adaptado
Um diagaram de blocos simplificado de um sistema de controle de malha fechada (de restroalimentação negativa) é mostrado na figura seguinte:
Sabendo-se que:
Obtenha a expressão do erro em estado estacionário para uma entrada degrau unitário.
Passo 1
Pelo diagrama temos que:
E:
Substituindo a primeira na segunda:
Portanto:
Passo 2
Substituindo as expressões das funções de transferência e a entrada degrau unitário:
Rearranjando:
Passo 3
Para encontrar a expressão para o erro em estado estacionário, devemos utilizar o teorema do valor final:
Resposta
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 7.1. Adaptado
Determine o erro em regime permanente para entradas de , e para o sistema mostrado abaixo. Sabendo que:
E que é o degrau unitário.
Passo 1
Pelo diagrama temos que:
E:
Substituindo a primeira na segunda:
Portanto:
Passo 2
Fazendo primeiramente para a entrada .
Substituindo o valor de que foi dado no enunciado e a entrada degrau, encontraremos a expressão do erro do sistema:
Rearranjando:
Aplicando o teorema do valor final:
Passo 3
Para a entrada :
Substituindo na expressão do erro:
Rearranjando:
E aplicando o teorema do valor final:
Passo 4
Por fim, para a entrada :
Então, a expressão de fica assim:
Rearranjando:
E aplicando o teorema do valor final:
Resposta
Para:
Esses resultados são coerentes visto que a função de transferência é do tipo 1.
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 7.1. Adaptado
Determine o erro em regime permanente para entradas de , e para o sistema mostrado abaixo. Sabendo que:
E que é o degrau unitário.
Passo 1
Primeiramente vamos relembrar como obter a expressão para o erro .
Pelo diagrama temos que:
E:
Substituindo a primeira na segunda:
Portanto:
Passo 2
Fazendo primeiramente para a entrada .
Substituindo o valor de que foi dado no enunciado e a entrada degrau, encontraremos a expressão do erro do sistema:
Rearranjando:
Aplicando o teorema do valor final:
Passo 3
Para a entrada :
Substituindo na expressão do erro:
Rearranjando:
E aplicando o teorema do valor final:
Passo 4
Por fim, para a entrada :
Então, a expressão de fica assim:
Rearranjando:
E aplicando o teorema do valor final:
Resposta
Para:
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 7.3
Um sistema com realimentação unitária possui a seguinte função de transferência:
Determine o valor de para resultar em um erro de em regime permanente. Considere uma entrada degrau unitário
Passo 1
A expressão para o erro para um feedback nós já encontramos:
Essa expressão foi deduzida na aula de erro em regime permanenre, caso você não lembre como chegamos nela, dá uma conferida lá e depois continua aqui.
Para esse caso amos considerar uma entrada defrau unitário, ou seja:
Nesse caso o enunciado nos disse claramente que a entrada era do tipo degrau, mas caso ele não falasse, nós poderíamos deduzir isso visto que a função de transferência é do tipo 0 e o erro no estado estacionário que desejamos é uma constante, Logo se a entrada fosse uma rampa, ou uma parábola o erro seria infinito, e se fosse um impulso, o erro seria 0.
Passo 2
Substituindo as funções de transferência na expressão do erro:
Para calcular o erro, aplicamos o teorema do valor final:
Passo 3
Como para aplicar o teorema do valor final, devemos levar a :
Resposta
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 7.4
Calcule o erro em regime permanente devido a uma perturbação degrau unitário para o sistema
Passo 1
Como vimos na aula de erros em regime permanente. O erro causado pelo distúrbio em uma malha do tipo da figura abaixo é sempre:
Ou ainda, dividindo numerador e denominador pela função :
Basicamente, o erro será inversamente proporcional às funções que estão à esquerda da entrada do distúrbio na malha, e diretamente proporcional às funções que estão à direita.
Passo 2
Substituindo os valores das funções:
Resposta
Exercício Resolvido #7
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 7.5. Adaptado
Determine o erro em regime permanente para uma entrada degrau unitário dado o sistema com realimentação não unitária da figura abaixo. Repita para uma entrada rampa.
Passo 1
Como a malha não é de realimentação unitária, não podemos usar a expressão que deduzimos para o erro para malha de realimentação unitária na aula sobre erros.
Então, vamos tentar chegar a expressão para o erro dessa malha do zero.
Para isso, vamos adicionar mais uma variável ao nosso diagrama de blocos, e vamos chamar nossos blocos genericamente de e :
Pelo diagrama de blocos temos que:
Multiplicando as duas expressões temos:
Passo 2
Além disso, também sabemos que:
Então, substituindo a expressão de :
Prontinho, já temos a expressão do erro para esse caso.
Passo 3
Substituindo os valores das funções de transferência e considerando degra unitário:
Aplicando o teorema do valor final:
Passo 4
Para a rampa:
Aplicando o teorema do valor final:
Resposta
Para:
Exercício Resolvido #8
Elaboração própria
Calcule o erro para uma perturbação do tipo degrau unitária na malha abaixo:
Primeiramente considere:
E depois considere:
Passo 1
Como já vimos na aula sobre erros em regime estacionário. O erro causado por um distúrbio numa malha desse tipo é igual a:
Rearranjando:
Então agora, só precisamos substituir as nossas funções de transferência e calcular os erros
Passo 2
Considerando :
Passo 3
Considerando :
Resposta
Para: