O efeito da adição de zeros e polos na função de transferência
Produzido por Alexandre NunesTeoria
Introdução
Agora que nós já vimos como se comportam e como são as respostas dos sistemas de primeira e segunda ordem, vamos continuar nossa jornada e tentar entender os sistemas de ordem superior.
Uma função de transferência normal pode ser descrita como:
Onde .
Nós já vimos as funções de primeira ordem, onde e , as de segunda ordem, com e . Nessa seção vamos analisar mais alguns casos além desses e ver como poderemos simplificá-los.
Só uma coisinha antes de começar: as raízes do polinômio do numerador são chamadas de zeros, enquanto as raízes do polinômio do denominador são chamadas de polos.
Sendo assim, as funções de transferência de primeira ordem têm um polo e nenhum zero, as funções de transferência de segunda ordem têm dois polos e nenhum zero.
Nosso objetivo aqui então vai ser entender qual será o efeito da adição de polos e zeros na nossa função de transferência. Tentaremos entender como eles impactam a resposta do processo e vamos tentar procurar casos para poder simplificar essas funções desconsiderando polos ou zeros.
Bora entrar nessa viagem?

Adição de um polo
Vamos considerar uma função de transferência de terceira ordem do tipo:
Considerando que os polos da função de transferência serão:
E
Ou seja, teremos dois polos imaginários referentes à equação do segundo grau do tipo subamortecida e um polo real .
Quando tivermos mais de dois polos, como é o caso aqui, será interessante para nós procurar por polos dominantes.
“Mas o que raios são polos dominantes?”
Calma, já te explico, mas antes vamos continuar analisando a nossa função de transferência.
Considerando uma entrada degrau unitário, teremos:
A inversa dessa função, no domínio tempo, será algo do tipo:
Os coeficientes , , e são resultantes da separação em frações parciais.
Não se assuste, você não precisa saber como fazer essa inversa, coloquei ela aqui só para a gente poder analisar o efeito dos polos na resposta final.
Vamos pensar juntos então. A adição do terceiro polo resultou na nossa resposta na adição de um termo . Esse por sua vez é um termo exponencial negativo, ou seja, quanto maior for o valor do expoente , menor será o valor do termo, e menos ele impactará na resposta final.
Sendo assim, quando o polo é muito maior do que os outros dois polos, nós podemos desconsiderar o polo que está mais afastado, reduzindo a função de transferência em uma função de transferência normal de segunda ordem. Os outros dois polos, então, são os polos dominantes que eu havia falado agora há pouco.
Essa aproximação é muito boa, pois quando podemos fazê-la, nós conseguimos calcular todos os parâmetros como overshoot, tempo de subida, tempo de sedimentação da mesma forma que calculamos para uma função de segunda ordem comum.
”Ok, mas como eu vou saber que um polo é suficientemente grande para poder desconsiderar”
Boa pergunta!
Bom, isso vai depender do seu grau de exigência, se você precisa de uma aproximação mais exata, você vai precisar que esse polo seja muito grande para poder desconsiderá-lo, agora se seu grau de exigência não é muito grande, polos um pouco maiores que os outros já serão suficientes.
De modo geral, um valor seguro para fazer a aproximação é quando o maior polo for cinco vezes maior que os outros polos. Nesses casos a aproximação pode ser feita sem medo, visto que uma diferença de cinco vezes é bastante coisa. Mas como eu disse, se o seu grau de exigência for menor, a aproximação pode ser feita para valores menores.
Só para exemplificar melhor, a figura abaixo apresenta três respostas. representa a resposta de uma função de transferência com apenas dois polos. representa uma função com os mesmos dois polos de e um terceiro polo muito maior que os outros dois. Por fim, a curva representa uma função com os dois polos de e um terceiro polo bem próximo dos outros dois.
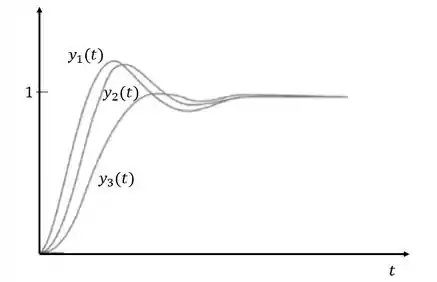
Repare que como o terceiro polo de é muito maior que os outros dois, a resposta é bem parecida com . O mesmo não acontece com cujo terceiro polo tem valor bem próximo dos outros dois.
Efeito do zero
Além da adição de polos à nossa função de transferência, também podemos ter casos em que são adicionados zeros. Por exemplo:
Os zeros, quando são adicionados em um sistema, afetam a amplitude, ou o overshoot, da resposta, mas não interferem em nada no tipo de resposta.
Portanto, se um sistema de segunda ordem é subamortecido sem nenhum zero, ao se adicionar um zero nesse sistema, ele continuará subamortecido.
Os zeros funcionam de maneira parecida com os polos. Quanto mais próximo for o zero dos polos, maior será o efeito sentido na resposta.
Quando os zeros se distanciam muito dos polos, seu efeito praticamente não é sentido e a função de transferência pode ser simplificada como uma função de transferência de segunda ordem comum.
Dessa forma, quando temos um zero próximo dos polos, a resposta transitória é levemente alterada, principalmente na amplitude e excesso (overshoot). Quando o zero se afasta muito dos polos, a resposta transitória é basicamente a mesma da função de transferência original, porém em uma versão em escala. Nesse caso, dizemos que o zero funciona como um fator de ganho.
Por exemplo, imagine uma função de segunda ordem.
Se adicionarmos um zero a essa função:
Se o zero for muito maior que os polos, ou seja, se for muito grande, a função de transferência pode ser simplificada como:
Portanto, quando o zero está muito longe dos polos, ele funciona como um termo multiplicativo da função de segunda ordem com dois polos, por isso que dizemos que ele funciona como um fator de ganho.
Existe ainda um outro caso em que é negativo, ou seja, o zero é positivo.
Quando isso acontece, a resposta transitória tende a desviar valor final no início antes de se aproximar dele. O gráfico abaixo mostra esse comportamento:
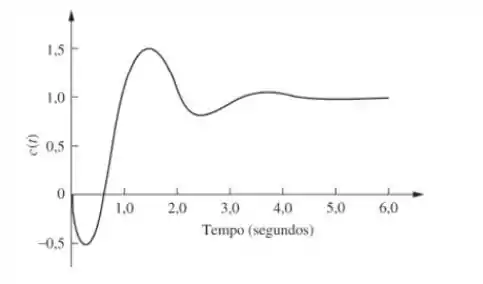
Na engenharia elétrica esse tipo de sistema é chamado de sistema de fase não mínima. Os sistemas de fase não mínima sempre começam agindo contrário ao desejado antes de começarem a corrigir a variável controlada. Sendo assim, se um avião funcionasse como um sistema de fase não mínima, e você comandasse que ele virasse para a esquerda, primeiramente ele viraria para a direita antes de virar para a esquerda.
Cancelamento de polos com zeros
Além dos casos onde existe um polo ou um zero muito longe da origem, uma outra forma de fazer aproximações em uma função de transferência com múltiplos polos e zeros é cancelando um polo com um zero.
Esse cancelamento pode ser feito quando existe um zero bem próximo de um polo. Para avaliar se o cancelamento pode ser feito, devemos fazer o seguinte procedimento.
Vamos usar como exemplo a função de transferência hipotética abaixo:
Vamos supor que a gente considera que o zero em é bem próximo do polo em , e por isso queremos saber se é possível fazer o cancelamento. Para isso, devemos expandir a função de transferência em suas frações parciais:
Onde , e são os coeficientes encontrados no processo de expansão em frações parciais. Para saber se o polo em pode ser cancelado com o zero em devemos avaliar o coeficiente referente a esse polo, ou seja, o coeficiente .
Portanto, para cancelar o polo com o zero, o coeficiente deve ser muito menor perto dos outros coeficientes ( e ). Se isso for verdade, podemos efetuar a simplificação e obteremos a função de transferência simplificada abaixo:
Adição de um polo
Efeito do zero
Cancelamento de polos com zeros
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 4.6a
Determine a validade de uma aproximação de segunda ordem para a função de transferência abaixo:
Passo 1
Para saber se podemos aproximar a função acima a uma função de transferência de segunda ordem, precisamos determinar o polos delas e ver se existe um que seja muito maior que os outros dois.
Um dos polos, é fácil de encontrar:
Passo 2
Vamos agora lembrar da nossa professora da oitava série e fazer Báskara para determinar os outrso dois polos:
Passo 3
Temos então um polo em e dois polos em . Para saber se podemos desconsiderar um desses polos, precisamos comparar a parte real desses polos.
Sendo assim, o polo em é mais de sete vezes maior que os outros dois polos (em módulo), o que faz com que esse polo possa ser desconsiderado.
Portanto, a aproximação é válida.
Resposta
Aproximação válida.
Exercício Resolvido #2
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 4.6b
Determine a validade de uma aproximação de segunda ordem para a função de transferência abaixo:
Passo 1
Vamos determinar os polos da função acima para saber se podemos aproximar ela de uma função de segunda ordem.
O polo de ordem 1 é fácil determinar:
Passo 2
Agora, vamos pegar o polo de segunda ordem e aplicar Báscara para determinar os outros dois polos da função de transferência.
Passo 3
Os nosso três polos são portanto:
Para saber se podemos aproximar precisamos ver quantas vezes o polo maior em módulo é maior que os outrs. Lembrando que para fazer essa comparação usamos sempre a parte real dos polos.
Sendo assim, podemos ver que o polo em é apenas quatro vezes maior que os outros dois polos, o que não produz uma aproximação muito boa para um modelo de segunda ordem.
Portanto, a aproximação não é válida.
Resposta
Aproximação não é válida.
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 4.10a. Adaptado
Para a função de transferência dada abaixo, determine se há cancelamento entre o zero e o polo mais próximo.
Passo 1
Vamo conferir se podemos cortar o zero em com o polo em (polo mais próximo do zero).
Para isso devemos fazer a expansão em frações parciais da função de transferência:
Passo 2
Vamos determinar os coeficientes , , e .
Se você não lembra da aula de cáluclo, vamos relembrar como fazemos isso. Para determinar um coeficiente a gente faz o limite da função antes da expansão sem o polo em questão tendendo ao valor do polo que foi retirado.
Assim ó:
Ou seja, para determinar o , a gente tirou o polo dele da função de transferência original, e fizemos que fosse igual a esse polo.
Para os outros coeficientes:
Passo 3
Sendo assim, a expansão em frações parciais será:
Para avaliar se podemos cancelar o polo em precisamos ver o seu coeficiente nas frações parciais, ou seja, o coeficiente .
Nos nossos cálculos o coeficiente deu , o que é bem próximo dos outros coeficientes (precisamos avaliar o valor absoluto), portanto, o polo em não pode ser cacelado.
Resposta
Aproximação não é válida.
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 4.10b. Adaptado
Para a função de transferência dada abaixo, determine se há cancelamento entre o zero e o polo mais próximo.
Passo 1
O polo mais próximo do zero em é o polo em . Vamos fazer a expansão em frações parciais da função de transferência para avaliar se o cancelamento pode ser feito ou não.
Passo 2
Vamos determinar os coeficientes , , e .
Para determinar esses coeficientes, a gente pega a função de transferência e retira dela o polo que a gente deseja determinar o coeficiente. Então, basta fazer a variável tender ao valor do polo que foi retirado.
Ou seja, para determinar o , a gente tirou o polo dele da função de transferência original, e fizemos que fosse igual a esse polo.
Para os outros coeficientes:
Passo 3
Sendo assim, a expansão em frações parciais será:
Repara que o coeficiente do polo foi muito pequeno, , que é menos de 5% do segundo menor coeficiente e por isso podemos fazer o cancelamento desse polo com o zero da função de transferência.
Sendo assim, a função de transferência aproximada seria:
Resposta
Aproximação é válida.
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 4.7a
Determine a validade de uma aproximação de respost ao degrau de segunda ordem para a função de transferência abaixo:
Passo 1
Para avaliar se podemos aproximar a função de transferência acima a uma de segunda ordem comum, precisamos verificar se o polo mais próximo do zero em poderá ou não ser cortado.
Para isso, vamos fazer a expansão em frações parciais:
Passo 2
Vamos determinar os coeficientes , e .
Usando o método de cacular os coeficientes da expansão em frações parciais:
Passo 3
Sendo assim, a expansão em frações parciais será:
Como podemos ver, o coeficiente do polo em , que é o polo mais próximo do zero, é cerca de 10% do valor dos outros polos. Apesar de ele ser bem pequeno, a aproximação para uma função de transferência ainda não é recoemendada.
Portanto, a aproximação não é válida.
Resposta
Aproximação não é válida.
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 4.7b
Determine a validade de uma aproximação de respost ao degrau de segunda ordem para a função de transferência abaixo:
Passo 1
O polo mais próximo do zero aqui é o polo em , então precisamos decidir se ele é próximo o suficiente para fazer o cancelamento.
Para isso, vamos fazer a expansão em frações parciais:
Passo 2
Vamos determinar os coeficientes , e .
Usando o método de cacular os coeficientes da expansão em frações parciais:
Passo 3
Sendo assim, a expansão em frações parciais será:
A expansão em frações parciais nos mostrou que o coeficiente do polo mais próximo do zero, o polo em , é muito pequeno perto dos outros dois coeficientes, portanto, é possível fazer o cancelamento do polo com o zero.
Portanto, a aproximação é válida.
Resposta
Aproximação é válida.
Exercício Resolvido #7
Elaboração própria
Avalie se é possível aproximar a função de transferência abaixo a uma função de transferência de segunda ordem. Se for possível, determine o overshoot e o tempo de assentamento (estabilização) para uma faixa de .
Passo 1
Primeiramente precisamos checar se é possível ou não fazer a aproximação. Como temos três polos, precisamos que um dos polos esteja muito mais afastado da origem que os outros dois. Os três polos são:
Como podemos ver o polo em está muito mais afastado que os outros dois. Ele é mais de seiscentas vezes maior que a parte real dos outros dois polos, o que faz com que ele seja uma ótima opção de cancelamento.
Sendo assim, a proximação é válida, e a função aproximada será:
Passo 2
Precisamos então calcular o overshoot e o tempo de assentamento. Para isso precisamos determinar a constante de tempo, , e o fator de amortecimento, da função de segunda ordem aproximada.
Precisamos comparar essa função de transferência com a função de transferência padrão de segunda ordem:
Sendo assim:
Passo 3
O cálculo do overshoot é dado pela fórmula abaixo:
Usando teremos:
E tempo de assentamento para uma faixa de pode ser calculado pela fórmula abaixo:
Com e :
Resposta
Aproximação é válida.
Exercício Resolvido #8
Elaboração própria
Avalie se é possível aproximar a função de transferência abaixo a uma função de transferência de segunda ordem. Se for possível, determine tipo de amortecimento e o tempo de assentamento (estabilização) para uma faixa de para a função de segunda ordem aproximada.
Passo 1
Primeiramente precisamos checar se é possível ou não fazer a aproximação. Nesse casos temos um polo muito perto do nosso zero, então vamos expandir a função de transferência em suas frações parciais:
Usando o método de cálculo dos coeficientes das frações parciais:
Podemos ver que o coeficiente , que é relativo ao polo mais perto do zero, , é muito menor que os outros dois coeficientes. Portanto, a aproximação de cancelamento polo-zero pode ser feita.
Sendo assim, a proximação é válida, e a função aproximada será:
Passo 2
Precisamos determinar o tipo de amortecimento e o tempo de assentamento da resposta aproximada. Para isso precisamos do tempo de amortecimento, , e contstante de tempo, . Para isso, vamos primeiro expandir a nossa função de transferência:
Precisamos comparar essa função de transferência com a função de transferência padrão de segunda ordem:
Então precisamos fazer umas manipulações:
Sendo assim:
Passo 3
Para determinar o tipo de assentamento, podemos usar o valor de e a figura abaixo:

Como o nosso fator de amortecimento está entre 0 e 1, a nossa resposta será subamorticida.
O tempo de assentamento para uma faixa de pode ser calculado pela fórmula abaixo:
Com e :
Resposta
Aproximação é válida.
Resposta subamortecida.