Sistemas de segunda ordem
Produzido por Alexandre NunesTeoria
Introdução
Agora que já matamos no peito e dominamos os processos caracterizados por funções de transferência de primeira ordem, vamos nos aprofundar e partir para os sistemas de segunda ordem.
Assim como as funções de transferência de primeira ordem eram originárias de equações diferenciais de primeira ordem, as funções de transferência de segunda ordem também serão originadas a partir de equações diferenciais de segunda ordem.
Então, seja a EDO de segunda ordem:
Aplicando a transformada de Laplace:
Colocando em evidência:
Para a função de transferência de segunda ordem, também teremos uma expressão padrão que será muito útil e que retornaremos nela muitas vezes:
Se nós compararmos o nosso exemplo genérico com a função de transferência padrão de segunda ordem, teremos:
Repare que dividimos tanto o numerador quando o denominador da função de transferência por para que conseguíssemos comparar a expressão da função de transferência com a expressão padrão.
Os parâmetros , e , assim como nos sistemas de primeira ordem, representam o ganho e a constante de tempo do processo. O parâmetro , é o fator de amortecimento do sistema e vamos nos aprofundar nele já já.
Tipos de respostas do sistema de segunda ordem
Os sistemas de segunda ordem, diferentemente dos sistemas de primeira ordem, podem apresentar diferentes tipos de respostas de acordo com as raízes do denominador da função de transferências.
Essas raízes, determinarão a razão de amortecimento do sistema.
Caso as raízes da equação quadrática do denominador sejam dois números reais diferentes, nós chamamos a resposta de superamortecida.
Se as raízes forem dois números reais iguais, nós chamaremos a resposta de criticamente amortecida.
Se as raízes forem dois números imaginários, a resposta será subamortecida.
Além disso, se as raízes forem dois números imaginários puros (parte real nula), a resposta é do tipo não-amortecida.
Obs: em todos os casos estamos considerando raízes reais negativas, ou imaginárias com partes reais negativas. Caso contrário, essa classificação não se aplica, e entenderemos mais para frente o porquê.
O fator de amortecimento, ,está diretamente relacionado com o tipo de resposta do sistema:

Resposta superamortecidas
Os sistemas superamortecidos são aqueles em que as raízes do polinômio do denominador da função de transferência são dois números reais negativos diferentes. Por exemplo:
Nesse exemplo, as raízes da expressão do denominador são e , logo, esse é um sistema superamortecido.
Os sistemas superamortecidos apresentam sempre . A gente pode comprovar isso no nosso exemplo expandindo a multiplicação do denominador e verificando o valor de
Comparando com a expressão padrão que vimos a cima, obtemos:
Então já vimos que os sistemas superamortecidos apresentam duas raízes reais negativas diferentes no polinômio do denominador, e que o seu fator de amortecimento, , sempre será maior que . Essas características fazem com que a resposta de um sistema de segunda ordem superamortecido seja sempre monótona (não-oscilatória).
Para uma entrada degrau, a expressão para a resposta fica:
Abrindo em frações parciais e calculando a inversa:
O desenvolvimento do cálculo da inversa aqui não é interessante, caso você não se lembre e tenha interesse em relembrar como fazer, a aula de Transformadas de Laplace explica bem esse cálculo.
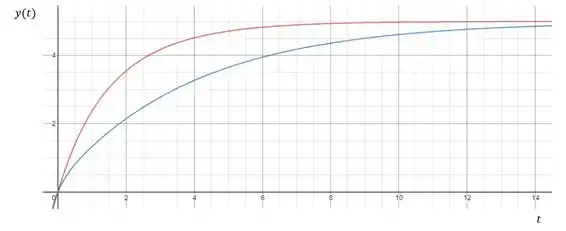
Esse é o gráfico para uma entrada degrau de uma função superamortecida. Como você pode notar, ela é monótona (não-oscilatória), e em , a resposta tende a estabilizar em um valor que é igual a (ganho vezes amplitude do degrau).
A linha azul e a linha vermelha representam dois processos superamortecidos com o mesmo ganho, , a mesma constante de tempo, , e a mesma amplitude de degrau, . O que difere os dois é o fator de amortecimento, . O processo da linha vermelha tem o fator de amortecimento igual a , enquanto o processo da linha azul tem fator de amortecimento igual a . Isso nos mostra que quanto maior o fator de amortecimento, maior vai ser a tendência da resposta se comportar como uma linha reta em vez de se comportar como uma exponencial. Ou seja, quanto maior o fator de amortecimento, , mais amortecido será a resposta.
Resposta subamortecidas
Os sistemas subamortecidos são os casos em que as raízes do polinômio do denominador da função de transferência são dois números imaginários com parte real negativa. Por exemplo:
Nesse caso, as raízes do polinômio são:
Como as raízes são dois números imaginários com parte real negativa, o sistema é subamortecido. Os sistemas subamortecidos tem fator de amortecimento, , entre e . Podemos verificar o fator de amortecimento do exemplo acima para comprovar isso:
A principal característica dos sistemas subamortecidos, é que devido às suas raízes imaginárias, as suas respostas são do tipo oscilatória.
Quanto menor for o fator de amortecimento do processo mais oscilatória será a resposta.
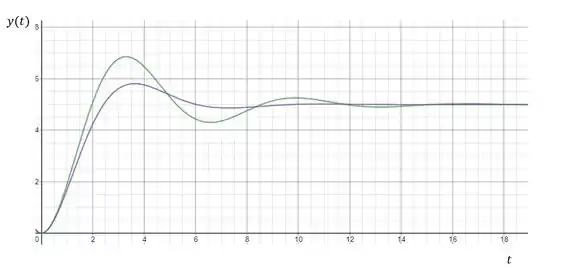
A figura mostra dois processo subamortecidos que possuem o mesmo ganho, , a mesma constante de tempo, , e submetidos a mesma variação degrau na entrada. Entretanto, o sistema da linha verde tem fator de amortecimento, , igual a , enquanto o da linha azul é igual a .
Pela imagem, percebemos que quanto menor o fator de amortecimento, maiores são as oscilações da resposta.
Para os sistemas subamortecidos, alguns parâmetros podem ser definidos:
- O overshoot pode ser definido como a razão entre o valor que o primeiro pico excede o valor do estado estacionário e a variação do estado estacionário. Ele pode ser aproximado como:
- A razão de declínio é a razão entre os valores de dois picos consecutivos, ela pode ser aproximada como o overshoot ao quadrado:
- O Período () é o tempo entre dois picos consecutivos ou dois vales consecutivos;
- O tempo de subida (), pode ser definido como o tempo que a resposta leva para ir de até da resposta final pela primeira vez, ou como o tempo que a resposta leva para atingir o valor do estado estacionário pela primeira vez. Pode ser aproximado como:
- O tempo de estabilização (), pode ser definido como o tempo que a resposta leva para ficar numa faixa de da resposta final. Ele pode ser aproximado como:
- O tempo até o primeiro pico ) pode ser aproximado como:
Casos intermediários
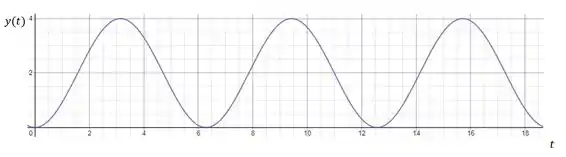
Existem alguns casos em que não é possível classificar um sistema como amortecido ou subamortecido. Esses casos são aquele onde =1 ou .
Quando , dizemos que o sistema é criticamente amortecido. Ou seja, ele tá no limite entre superamortecido e subamortecido. Se mexermos um cabelímetro na nossa função de transfeência ele se torna um dos dois casos. Os sistemas criticamente amortecidos são aqueles em que as raízes do denominador são dois números reais negativos iguais, Por exemplo:
O gráfico para a resposta dos sistemas criticamente amortecidos tem a seguinte forma:
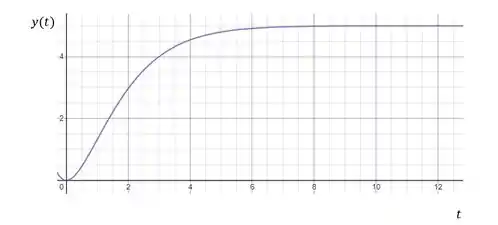
Eles são muito parecidos com os superamortecidos, mas se o fator de amortecimento deles diminuir um pouquinho, eles já começam a oscilar, mesmo que bem pouco.
Outro caso intermediário é quando o fator de amortecimento, , é igual a . Esse caso acontece quando a parte real das raízes imaginárias do polinômio do denominador é nula. Por exemplo:
Nesses casos, as oscilações da resposta não diminuem: