Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformada de Laplace e Função de Transferência

Ver Todos os Exercícios

Teoria

Transformada de Laplace

Seria bom aprender ferramentas para facilitar a resolução de equações diferenciais né?

Em controle clássico, utilizamos com frequência uma dessas ferramentas, a Transformada de Laplace. Ela consegue transformar equações diferenciais desse tipo:

y ¨ + 2 ζ ω n y ˙ + ω n 2 y = 0

Com soluções difíceis e podendo ter essa cara:

y t = ω n 1 - ζ 2 e - ζ ω n t sen ⁡ ω n ( 1 - ζ 2 t )   ,   s e n d o   ζ < 1

Em uma divisão de polinômios, mais fácil de resolver:

Y s = ω n 2 s 2 + 2 ζ ω n s + ω n 2

Ok, e como isso corre?

Através desse teorema que relaciona uma função no domínio da frequência com outra no domínio do tempo.

L f t = F s = ∫ 0 - ∞ f t e - s t d t   ,   s e n d o   s = σ + j ω

Assim ela não parece que facilita nossa vida, rs.

Na prática, por exemplo, verificamos o seguinte ao realizarmos uma Transformada de Laplace de uma função exponencial.

f t = e - a t

Que no domínio da frequência é:

F s = 1 s + a

Ou seja, uma divisão de polinômios com um polinômio de grau zero em cima e um de grau um embaixo. Essa agora vai ser nossa realidade, trocar funções exponenciais e periódicas por uma função com divisão de polinômios.

f t = sen ⁡ ω t     ⟷     F s = ω s 2 + ω 2

f t = cos ⁡ ω t     ⟷     F s = s s 2 + ω 2

Mas relaxe, nem sempre vamos precisar usar a definição para encontrar uma transformada de Laplace, muitas vezes vamos poder usar uma tabela como essa aqui:

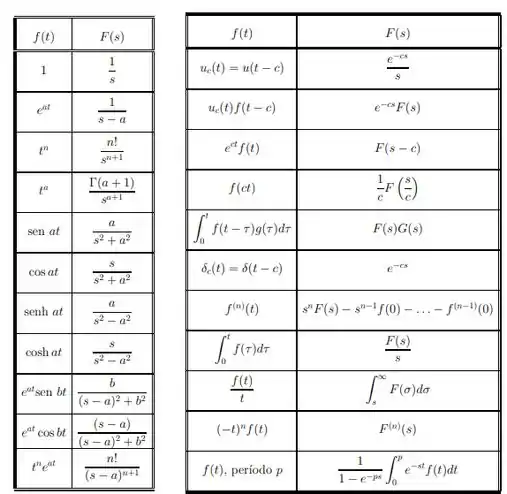
Propriedades Transformada de Laplace

Para que essa mágica ocorra, é importante estarmos familiarizados com as propriedades das Transformadas de Laplace. As principais estão abaixo:

Para começarmos a nos entrosar com as propriedades, vamos utilizar o sistema de segunda ordem do início da teoria com ω n = 4 e ζ = 0,5 e com uma força externa F t = 10

y ¨ + 2.0,5.4 y ˙ + 4 2 y = F ( t )  

y ¨ + 4 y ˙ + 16 y = 10

Passando do domínio do tempo para frequência e com isso utilizando as propriedades 4, 3 e 1

s 2 Y s - s y 0 + - y ˙ 0 + ⏟ P r o p r i e d a d e   4 + 4 [ s Y s - y 0 + ] ⏟ P r o p r i e d a d e   3 + 16 Y ( s ) ⏟ P r o p r i e d a d e   1 =   10 ⏟ P r o p r i e d a d e   1

Nesse caso considerando condições iniciais nulas, y ˙ 0 + = y 0 + = 0 .

s 2 Y s + 4 s Y s + 16 Y s = 10

Colocando o Y s em evidência.

Y s . s 2 + 4 s + 16 = 10

Passando o polinômio para o outro lado da igualdade.

Y s = 10 s 2 + 4 s + 16

Chegamos assim, na resposta do sistema no domínio da frequência.

O passo a passo para vitória quando utilizar a transformada de Laplace é:

  1. Obter as equações diferenciais linearizadas.
  2. Obter a transformada de Laplace das equações diferenciais.
  3. Resolver a equação algébrica resultante para a transformada de variável de interesse.

Transformada Inversa de Laplace

Como nosso mundo ocorre no domínio do tempo, a transformada de Laplace nos facilita resolver as equações diferenciais, mas depois de conseguirmos a solução, muitas vezes precisamos expressar a solução no domínio do tempo.

Para que isso ocorra, utilizamos a transformada inversa de Laplace:

L - 1 F s = f t = 1 2 π j ∫ c - j ∞ c + j ∞ F s e s t d s   ,   p a r a   t > 0

Esse susto nós já tomamos hoje, kkkkkk.

Para utilizar a transformada inversa de Laplace, o que vamos fazer é utilizar o velho conhecido método das frações parciais na função Y ( s ) e depois olharmos em tabelas de transformada de Laplace, qual a equivalente dos termos em destaque no domínio do tempo.

Sendo:

Y s = s + 3 s + 1 s + 2

Ao realizarmos o método das frações parciais, resulta:

Y s = k 1 s + 1 + k 2 s + 2

Em que k 1 e k 2 são conhecidos como resíduos. Para calcular eles, fazemos o seguinte:

k 1 = s - s 1 p s q s s = s 1

e

k 2 =   s - s 2 p s q s s = s 2

Em que s 1 é a raiz do denominador do primeiro termo s + 1   e s 2 é a raiz do denominador do segundo termo ( s + 2 ) e p ( s ) o polinômio do numerador de Y ( s ) e q ( s ) o polinômio do denominador de Y ( s ) .

Atribuindo os respectivos valores para k 1 e k 2 .

k 1 = s + 1 ( s + 3 ) ( s + 1 ) ( s + 2 ) s = - 1 = 2

    k 2 = s + 2 ( s + 3 ) ( s + 1 ) ( s + 2 ) s = - 2 = - 1

Com os valores de k 1 e k 2 e substituindo em Y ( s ) .

Y s = 2 s + 1 + - 1 s + 2

Olhando em qualquer tabela de pares de Transformada de Laplace, verificamos que:

y t = e - a t   ⇒                         L a p l a c e                       Y s = 1 s + a

y t = e - a t   ⇐ I n v e r s a   d e   L a p l a c e Y s = 1 s + a

Então, L - 1 Y s = L - 1 2 s + 1 + L - 1 - 1 s + 2

Como as propriedades da Transformada de Laplace funcionam de forma semelhante para a Transformada Inversa de Laplace.

L - 1 Y s = 2 L - 1 1 s + 1 - 1 L - 1 1 s + 2

L - 1 Y s = y t = 2 e - t - 1 e - 2 t

Com isso, conseguimos nosso resultado em função do tempo.

Função de Transferência

Um sistema com a seguinte equação do movimento:

10 θ ¨ + 5 θ ˙ = f t       ,       c o m   θ ˙ 0 + = θ 0 + = f 0 + = 0

Pode ser representado no domínio da frequência como:

10 s 2 Θ s - s θ 0 + - θ ˙ 0 + + 5 s Θ s - θ 0 + = F ( s )

10 s 2 Θ s + 5 s Θ s = F ( S )

Θ s F s = 1 10 s 2 + 5 s = H ( s )

A função de transferência de um sistema linear, H s ,   é a relação entre a transformada de Laplace do sinal de saída pela transformada de Laplace da variável de entrada, com todas as condições iniciais nulas.

Ela é uma forma de representar a dinâmica do sistema. E só pode ser definida em um sistema linear e invariante no tempo. Lembre-se dessa condição, costuma cair com frequência em provas.

Outro detalhe importante sobre a função de transferência é que a ordem do polinômio do numerador deve ser menor ou igual ao do polinômio do denominador.

H s = Y s X s = b 0 s m + b 1 s m - 1 + … + b m - 1 s + b m a 0 s n + a 1 s n - 1 + … + a n - 1 s + a n         ,   s e n d o   q u e   n ≥ m

Agora é praticar!

Propriedades Transformada de Laplace

Transformada Inversa de Laplace

Função de Transferência

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Seja a função f t = e - 2 t sen ⁡ 4 t , encontre a Transformada de Laplace de f ( t ) .

Passo 1

E aí galera, em questões de ter que encontrar a Transformada de Laplace, já partimos verificar quais propriedades podem deixar a questão mais clara.

Nesse caso verificaríamos a propriedade

L e - α t f t = F s + a

Após encontrar a propriedade com semelhança a estrutura que temos, verificamos qual dos pares de transformada de Laplace correspondem ao f ( t ) .

Nesse caso, f t = sen ⁡ ω t e F s = ω s 2 + ω 2 .

Com essas correlações em mão, só substituir e ser feliz.

Passo 2

Com a propriedade correspondente a f ( t ) verificada, substituímos os valores.

L e - α t f t = F s + a

L e - 2 t f t = F s + 2

Depois, como conseguimos verificar nas tabelas de pares de transformadas que

  L sen ⁡ ω t = ω s 2 + ω 2

Então,

L e - 2 t sen ⁡ 4 t = 4 s + 2 2 + 4 2

F s = 4 s + 2 2 + 4 2

Resposta

F s = 4 s + 2 2 + 4 2

Exercício Resolvido #2

Elaboração própria

Seja a função F ( s ) = 1 s s + 3 qual é o lim t → ∞ ⁡ f ( t ) ?

Passo 1

Qualquer questão que falar de tempo no infinito já vamos testar o Teorema do Valor Final (TVF).

Importante sempre que aplicarmos o TVF fazer isso, é verificar se o lim t → ∞ ⁡ f ( t )   existe.

Passo 2

Aplicando o TVF verificamos que:

lim t → ∞ ⁡ f ( t ) = lim s → 0 ⁡ s F ( s )

Então,

lim s → 0 ⁡ s F ( s ) = lim s → 0 ⁡ s 1 s s + 3 = lim s → 0 ⁡ 1 s + 3 = 1 3

Verificando se o lim t → ∞ ⁡ f t existe, verificamos se a raiz de s + 3 é um número real negativo.

s + 3 = 0

s = - 3

Logo, o lim t → ∞ ⁡ f ( t ) existe.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, Exemplo 2-1.3

Obtenha a transformada de Laplace da seguinte função:

c t = u t - 3 1 - e - t - 3 4  

Passo 1

Para resolver essa questão, vamos usar e abusar das propriedades das transformadas de Laplace, mas antes disso, vamos fazer uma mudança de variáveis.

Vamos falar que:

c t = f ( t - 3 )

Sendo assim, a nossa função f t será:

f t = u t 1 - e - t 4

f t = u t - u t e - t 4

Então, primeiro vamos achar a transformada de f ( t ) e depois achamos a transformada de f ( t - 3 ) .

Passo 2

Bora achar a transformada de f ( t ) então:

F s = L u t - u t e - t 4

Usando a propriedade da linearidade, podemos dizer que:

F s = L u t - L u t e - t 4

A primeira parcela da transformada, é a função degrau, que tem transformada conhecida e igual a 1 s :

F s = 1 s - L u t e - t 4

Para a segunda parcela, vamos usar essa propriedade aqui:

L f t e a t = F ( s - a )

Como a transformada de u ( t ) é 1 s , e nesse caso a constante a é - 1 4 , teremos:

F s = 1 s - 1 s + 1 4

Rearranjando:

F s = 1 s 4 s + 1

Passo 3

Agora, precisamos encontrar a transformada de f ( t - 3 ) , para isso, vamos usar a seguinte propriedade:

L f t - 3 = e - 3 s F ( s )

Como F s = 1 s 4 s + 1 :

L f t - 3 = e - 3 s s 4 s + 1

Passo 4

E como definimos lá no início que:

c t = f ( t - 3 )

L c ( t ) = L f t - 3

Portanto:

C s = e - 3 s s 4 s + 1

Resposta

C s = e - 3 s s 4 s + 1

Exercício Resolvido #4

USP – P1.2016 – Q.2 - Prof. Hélio Mitio Morishita

Obter o valor de lim t → ∞ ⁡ y ( t ) , se houver, para as funções abaixo, justificando a resposta. Em todos os casos a   ∈   R e impor as condições necessárias sobre o parâmetro da equação quando for o caso.

a) Y s = 1 s + a s - a . 1 s  

b) Y s = s - a s + a . 1 s

c) Y s = 1 s + a . ω s 2 + ω 2

Passo 1

Falou de valor de lim t → ∞ ⁡ y ( t ) , já podemos abrir o sorriso. Pois poderemos utilizar o TVF.

lim t → ∞ ⁡ f ( t ) = lim s → 0 ⁡ s F ( s )

Contudo, devemos lembrar que para aplicar o Teorema do Valor Final (TVF) e o lim t → ∞ ⁡ f t exista, precisamos verificar duas condições:

1) As raízes do denominador do lim s → 0 ⁡ s F ( s ) , devem ter parte real negativa.

2) O sinal de excitação deve ser limitado.

Agora vamos lá verificar essas condições.

Passo 2

a) Aplicando o TVF:

lim s → 0 ⁡ s F ( s ) = lim s → 0 ⁡ s 1 s + a s - a . 1 s   = lim s → 0 ⁡ 1 s + a s - a = - 1 a 2

Contudo ao verificar as condições para que o lim t → ∞ ⁡ f t exista, verificamos as raízes do polinômio s + a s - a são:

s 1 = + a   ,   s 2 = - a

Como existe raízes do polinômio do denominador com raízes positivas, o lim t → ∞ ⁡ f t não existe.

Passo 3

b) Aplicando o TVF:

lim s → 0 ⁡ s F ( s ) = lim s → 0 ⁡ s s - a s + a . 1 s   = lim s → 0 ⁡ s - a s + a = - 1

Verificando as condições para que o lim t → ∞ ⁡ f t exista:

1) A raiz do polinômio s + a é s 1 = - a , logo sendo parte real negativa, essa condição está satisfeita.

2)O sinal de excitação nesse contexto é o termo:

X s = 1 s

Que está multiplicado ao termo:

H s = s - a s + a

Como X ( s ) é o sinal de excitação degrau unitário, um sinal limitado, essa condição também está satisfeita.

Logo, lim t → ∞ ⁡ f t =   - 1

Passo 4

c) Aplicando o TVF:

lim s → 0 ⁡ s F ( s ) = lim s → 0 ⁡ s 1 s + a . ω s 2 + ω 2   = lim s → 0 ⁡ s s + a . ω s 2 + ω 2 = 0

Verificando as condições para que o lim t → ∞ ⁡ f t exista:

1) A raiz do polinômio s + a ( s 2 + ω 2 ) é s 1 = - a , s 2 , s 3 =   ± i ω , como s 2 , s 3 não tem parte real negativa, esta condição não está satisfeita.

2)O sinal de excitação nesse contexto é o termo:

X s = ω s 2 + ω 2

Que está multiplicado ao termo:

H s = 1 s + a

Como X ( s ) é o sinal de excitação harmônico, um sinal não limitado, essa condição também não está satisfeita.

Então, o lim t → ∞ ⁡ f t não existe.

Resposta

a )   lim t → ∞ ⁡ f t não existe.

b) lim t → ∞ ⁡ f t =   - 1 .

c)     lim t → ∞ ⁡ f t não existe.

Exercício Resolvido #5

Elaboração própria

Ache a inversa de Laplace da seguinte equação:

Y s = 1 s s + 1 3

Passo 1

E aí pessoal, tudo tranquilo?

Nessa questão para resolvermos a inversa de Laplace precisamos abrir em frações parciais e nesse caso ocorrerá uma equação com raízes múltiplas.

Após achar os coeficientes de cada termo da expansão em frações parciais precisamos verificar qual seu equivalente no domínio do tempo e ai fim do jogo! 😊

Passo 2

Abrindo Y s em frações parciais teremos a seguinte relação:

Y s = 1 s s + 1 3 = A s + B s + 1 + C s + 1 2 + D s + 1 3

As raízes do polinômio no denominador são: s 1 = 0 e s 2 , s 3 , s 4 = - 1 .

Para resolvermos para os coeficientes A e D é a forma usual, mas para B e C é um jeito um pouco diferente.

Vamos começar por A e D que já conhecemos.

Logo, multiplicamos todos os termos pela respectiva equação do denominador do coeficiente que queremos descobrir o valor e depois fazemos o limite tender para a raiz dessa equação.

Para determinar A:

Multiplicamos todos os termos pela respectiva equação do seu denominador.

s Y s = s . 1 s s + 1 3 = s A s + s B s + 1 + s C s + 1 2 + s D s + 1 3

Agora fazemos o limite para o valor de sua raiz.

lim s → 0 ⁡ s Y ( s ) = lim s → 0 ⁡ 1 s + 1 3 = lim s → 0 ⁡ A + s B s + 1 + s C s + 1 2 + s D s + 1 3

Logo,

A = 1

Para determinar D:

Multiplicamos todos os termos pela respectiva equação do seu denominador.

s + 1 3 Y s = s + 1 3 . 1 s s + 1 3 = s + 1 3 A s + s + 1 3 B s + 1 + s + 1 3 C s + 1 2 + s + 1 3 D s + 1 3

Agora fazemos o limite para o valor de sua raiz.

lim s → - 1 ⁡ s + 1 3 Y ( s ) = lim s → - 1 ⁡ 1 s = lim s → - 1 ⁡ s + 1 3 A s + s + 1 3 B s + 1 + s + 1 3 C s + 1 2 + D

Portanto,

D = - 1

Passo 3

Agora, para acharmos os coeficientes B e C, fazemos a seguinte receita de bolo:

1) Pegamos a função s + 1 3 Y ( s ) e derivamos ela uma vez para encontrar C e duas vezes para encontrar B.

2)Aplicamos o limite tendendo para a raiz s = - 1 .

Passo 4

Determinando C:

1)

d d s s + 1 3 Y s = d d s s + 1 3 A s + s + 1 3 B s + 1 + s + 1 3 C s + 1 2 + D

d d s s + 1 3 . 1 s s + 1 3 = d d s s + 1 3 A s + s + 1 2 B + s + 1 1 C + D

- 1 s 2 = 3 s + 1 2 A s - s + 1 3 A s 2 + 2 s + 1 B + C

2)

lim s → - 1 ⁡ - 1 s 2 = lim s → - 1 ⁡ 3 s + 1 2 A s - s + 1 3 A s 2 + 2 s + 1 B + C

Assim,

C = - 1

Passo 5

Determinando D:

1)

d 2 d s 2 s + 1 3 Y s = d 2 d s 2 s + 1 3 A s + s + 1 3 B s + 1 + s + 1 3 C s + 1 2 + D

d 2 d s 2 s + 1 3 . 1 s s + 1 3 = d 2 d s 2 s + 1 3 A s + s + 1 2 B + s + 1 1 C + D

2 s 3 = d d s 3 s + 1 2 A s - s + 1 3 A s 2 + 2 B

Como o termo ( s + 1 ) vai continuar existindo depois de efetuar a derivada:

d d s 3 s + 1 2 A s - s + 1 3 A s 2

Não é necessário efetuar essa operação.

2)

lim s → - 1 ⁡ 2 s 3 = lim s → - 1 ⁡ d d s 3 s + 1 2 A s - s + 1 3 A s 2 + 2 B

Assim,

2 - 1 3 = 2 B

B =   - 1

Passo 6

Agora que temos nossos coeficientes definidos.

Y s = 1 s - 1 s + 1 - 1 s + 1 2 - 1 s + 1 3

Só aplicar a transformada inversa de Laplace:

L - 1 Y s = L - 1 1 s - L - 1 1 s + 1 - L - 1 1 s + 1 2 - L - 1 1 s + 1 3

Verificando em qualquer tabela de transformadas, verificamos que:

y t = 1 - e - t - t e - t - t 2 e - t 2

Que pode ser rescrita como:

y t = 1 - e - t 1 + t + t 2 2

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #6

Elaboração própria

Ache a inversa de Laplace da seguinte equação:

Y s = 2 s ( s 2 + 2 s + 2 )

Passo 1

Falaaa... beleza???? Vamos fazer essa inversa aqui juntos?? Então bora...

A primeira coisa que vamos fazer é dividir em frações parciais, que vai ficar assim: (repara bem quando o polinômio embaixo é de segundo grau, em cima vai ter um do primeiro grau...)

2 s s 2 + 2 s + 2 = A s + B s + C s 2 + 2 s + 2

E vamos usar a tabela de transformadas:

E vamos fazer uma pré seleção das que parecem mais com as do nosso problema:

f t = 1 → F s = 1 s

f t = e a t sin ⁡ b t → F s = b s - a 2 + b 2

f t = e a t cos ⁡ b t → F s = s - a s - a 2 + b 2

Passo 2

Vamos achar os A , B   e   C , então:

2 = A s 2 + 2 s + 2 + B s + C s

2 = A s 2 + 2 A s + 2 A + B s 2 + C s

2 = A + B s 2 + 2 A + C s + 2 A

E ficamos com o sisteminha: (igualando o que ta na frente do s 2 de um lado e do outro, do s e os que não têm s )

A + B = 0 2 A + C = 0 2 A = 2

E achamos:

2 A = 2

A = 1

A + B = 0

1 + B = 0

B = - 1

2 A + C = 0

2 1 + C = 0

C = - 2

Então ficamos com:

2 s s 2 + 2 s + 2 = A s + B s + C s 2 + 2 s + 2

2 s s 2 + 2 s + 2 = 1 s - s + 2 s 2 + 2 s + 2

A gente vai precisar achar a inversa de 1 s e de s + 2 s 2 + 2 s + 2 .

Pra 1 s é só ver:

f t = 1 → F s = 1 s

Então:

L - 1 1 s = 1

Passo 3

E pra outra vamos precisar fazer algumas manipulaçõezinhas...

Primeiro a gente quer deixar parecido com:

f t = e a t cos ⁡ b t → F s = s - a s - a 2 + b 2

(a gente sempre começa com o “s”, que a do cosseno, porque depois é só ir adicinando alguma coisa e vai dar a do seno)

s + 2 s 2 + 2 s + 2 = ?

A gente pode reescrever assim, oh:

s + 2 s 2 + 2 s + 2 = s + 1 + 1 s + 1 2 + 1

E dá pra dividir em duas, ainda:

s + 2 s 2 + 2 s + 2 = s + 1 s + 1 2 + 1 + 1 s + 1 2 + 1

Passo 4

Vamos pegar a primeira parcela da soma: s + 1 s + 1 2 + 1

Repara que temos o caso a = - 1 e b = 1 , então vamos ter:

L - 1 s + 1 s + 1 2 + 1 = e - 1 t cos ⁡ 1 t

L - 1 s + 1 s + 1 2 + 1 = e - t cos ⁡ t

Já pra segunda parcela: 1 s + 1 2 + 1

Agora vamos relacionar com o seno:

L - 1 1 s + 1 2 + 1 = e - t sin ⁡ t

Entãããooo agora é só somar tudo (ou diminuir porque tem um sinal de menos... só ter atenção):

L - 1 2 s s 2 + 2 s + 2 = L - 1 1 s - L - 1 s + 1 s + 1 2 + 1 + L - 1 1 s + 1 2 + 1

L - 1 2 s s 2 + 2 s + 2 = 1 - e - t cos ⁡ t + sin ⁡ t

E acabamos... dá um trabalhinho, mas a gente chega, viu?

Resposta

L - 1 2 s s 2 + 2 s + 2 = 1 - e - t cos ⁡ t + sin ⁡ t

Exercício Resolvido #7

UFF – Lista 1 – 2015.2 – Profa. Ninoska Bojorge

Resolva a equação diferencial ordinária abaixo pelo método da transformada de Laplace:

y ¨ + y = 4 δ t - 2 π com y 0 = 1 e y ˙ 0 = 0

Passo 1

Show, vamos resolver essa equação diferencial ordinária (EDO) de boas!

Quando temos que resolver EDO como essa de cima, começamos rescrevendo a EDO colocando todos os termos semelhantes de um mesmo lado, caso seja possível.

Depois aplicamos a transformada de Laplace e utilizamos suas propriedades para arrumarmos a equação e encontrarmos a solução de   Y ( s ) . Após termos encontrado a solução de Y ( s ) , no domínio da frequência, aplicamos a transformada inversa de Laplace para conseguirmos a resposta no domínio do tempo.

Passo 2

Temos então a seguinte EDO: y ¨ + y = 4 δ t - 2 π com y 0 = 1 e y ˙ 0 = 0

Lembrando que δ ( t ) é a função impulso, que tem como L δ t = 1 .

Nessa questão também iremos utilizar a propriedade:

L e - α t f t = F s + a

Aplicando a transformada de Laplace temos:

s 2 Y s - s y 0 + - y ˙ 0 + + Y s = 4 e - 2 π s

Como y 0 = 1 e y ˙ 0 = 0

s 2 Y s - s 1 - 0 + Y s = 4 e - 2 π s

Y s s 2 + 1 = s + 4 e - 2 π s

Y s = s s 2 + 1 + 4 e - 2 π s s 2 + 1

Y s = s s 2 + 1 + 4 1 s 2 + 1 e - 2 π s

Passo 3

Aplicando a transformada inversa de Laplace, temos:

L - 1 Y s = L - 1 s s 2 + 1 + 4 L - 1 1 s 2 + 1 e - 2 π s

Observando a propriedade da transformada de Laplace:

L f t - α μ - 1 ( t - a ) = e - α t F s

E as seguintes transformadas de Laplace:

L [ sen ⁡ ω t ] = 1 s 2 + ω 2

L [ cos ⁡ ω t ] = ω s 2 + ω 2

Para o primeiro termo temos:

L - 1 s s 2 + 1 = cos ⁡ 1 . t

E para o segundo termo:

4 L - 1 1 s 2 + 1 e - 2 π s ⏟ P r o p r i e d a d e = 4 sen ⁡ t - 2 π

Substituindo os resultados em y ( t ) .

y t = cos ⁡ t + 4 sen ⁡ t - 2 π . u - 1 ( t - 2 π )

Sendo a função u - 1 t - 2 π a função degrau unitário definida como

u - 1 t - 2 π = 0 ,     0 ≤ t < 2 π 1 ,     t ≥ 2 π

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

USP – P1.2017 – Prof. Hélio Mitio Morishita

Considere a seguinte função de transferência:

Y s R ( s ) = s + a s + b s + c   c o m   a ∈ R ,   b   e   c ∈   R +

Pede-se:

  1. Exprimir a equação diferencial correspondente;
  2. A transformada inversa de Laplace para obter y ( t ) considera a parte homogênea da equação diferencial? Se sim, indique quais são estes termos, admitindo que R ( s ) seja uma função degrau unitário.

Passo 1

Então galera, para fazer essa questão precisamos lembrar que toda equação diferencial tem em sua resposta um termo relacionado ao regime transitório e outro relacionado ao regime permanente.

y t = y h o m o g ê n e a t + y p a r t i c u l a r ( t )

Nesse caso o termo relacionado ao regime transitório é o y h o m o g ê n e a ( t ) é o termo relacionado ao regime permanente é y p a r t i c u l a r ( t ) .

E que a função de transferência é a relação entre a equação diferencial de saída pela excitação.

Y s = H s . X ( s )

Agora vamos ver como isso se encaixa com as questões do enunciado.

Passo 2

a) Sendo,

Y s R s = s + a ( s + b ) ( s + c )

Rearrumando:

Y s . s 2 + b c s + b c = R ( s ) ( s + a )

Separando as variáveis.

Y s s 2 + Y s s b + c + Y s b c = R s s + R s a

Como pela definição de função de transferência, as condições iniciais são consideradas nulas.

y ˙ 0 + = 0 ,   y 0 + = 0

Conseguimos fazer aparecer a estrutura abaixo:

Y s s 2 - s 0 - 0 + b + c Y s s - s 0 + Y s b c = [ R s s - 0 ] + R s a

[ Y s s 2 - s y 0 + - y ˙ ( 0 + ) + ( b + c ) [ Y s s - s y 0 + ] + Y s b c = [ R s s - r ( 0 + ] ) + R s a

Que pela inversa da transformada de Laplace conseguimos:

y ¨ t + y ˙ t b + c + y t b c = r ˙ t + a r ( t )

Passo 3

b) A transformada inversa de Laplace para obter y ( t ) considera a parte homogênea da equação diferencial? Se sim, indique quais são estes termos, admitindo que R ( s ) seja uma função degrau unitário.

Então, para conseguirmos saber o que responder, olhamos para nossa função de transferência H ( s ) .

Y s = H s . X ( s )

Como,

H s = s + a ( s + b ) ( s + c )

Ao excitarmos o sistema com um degrau unitário, o que é nossa primeira tentativa normalmente quando vamos analisar a resposta de um sistema a uma excitação.

X s = 1 s

Y s = s + a s + b s + c . 1 s

Ao expandir em frações parciais:

s + a s + b s + c . 1 s = A s + b + B s + c + C s

Igualando os denominadores resulta em:

s + a s + b s + c . 1 s = A s + c s s + c s + b s + B s + b s s s + c s + b + C ( s + b ) ( s + c ) s s + c s + b

s + a = A s + c s + B s + b s + C ( s + b ) ( s + c )

Para s = - b :

- b + a = A - b + c ( - b ) + B - b + b ( - b ) + C ( - b + b ) ( - b + c )

- b + a = A - b + c ( - b )

A = - b + a - b + c - b

Para s = - c :

- c + a = A - c + c ( - c ) + B - c + b ( - c ) + C ( - c + b ) ( - c + c )

- c + a = B - c + b ( - c )

B = - c + a - c + b - c

Para s = 0 :

0 + a = A 0 + c ( 0 ) + B 0 + b ( 0 ) + C ( 0 + b ) ( 0 + c )

a = C b ( c )

C = a b c

Substituindo o valor das variáveis A , B   e   C em Y ( s ) .

Y s = - b + a - b + c - b 1 s + b + - c + a - c + b - c 1 s + c + a b c 1 s

Fazendo a transformada inversa de Laplace de Y ( s ) .

L - 1 Y s = - b + a - b + c - b . e - b t + - c + a - c + b - c . e - c t + a b c

Os termos que contêm a exponencial elevado a um valor negativo, são os termos associados a resposta homogênea e o termo constante é o associado a resposta particular.

Resposta

Ei, a resposta está no passo a passo :)