Amostragem
Teoria
Introdução
Tudo que estudamos de controle até aqui, nós estudamos sob a ótica do controle analógico. O controle analógico funciona sempre com sistemas contínuos no tempo.
Se desejarmos usar um controlador digital na nossa planta, precisamos converter o sinal analógico para um sinal digital fazendo uso de um conversor A/D, que é formado por um amostrador e por um retentor.
Dessa forma, precisamos, por exemplo fazer com que um sinal seja transformado de contínuo para discreto. Esse procedimento é chamado de amostragem.
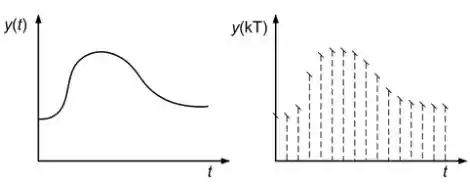
Para realizar a amostragem, utiliza-se um equipamento que chamamos de amostrador, no diagrama de blocos esse instrumento será representado da seguinte forma:
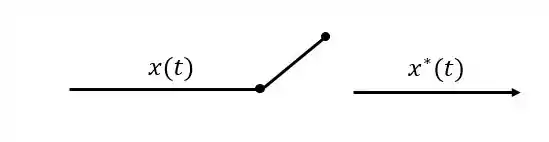
O amostrador funciona da seguinte forma: a chave fechará a intervalos constantes de tempo (). Quando a chave fecha, o sinal naquele momento da função é transmitido para o restante do sistema, como se o amostrador tirasse uma foto do sinal a intervalo regulares de tempo. Quando a chave está aberta, esse sinal é . Dessa forma, é possível fazer com que um sinal contínuo seja discretizado.
Para facilitar o nosso lado, vamos sempre considerar que o amostrador que estamos usando é ideal. Isso quer dizer que o nosso amostrador fica fechado por um tempo muito curto, um infinitésimo de segundo. Dessa forma, é como se quando a chave do amostrador fechasse, ele “tirasse uma foto” do sinal contínuo naquele momento. Deu pra pegar a ideia?
Vamos ver agora, matematicamente, como a amostragem de uma função contínua é feita, mas antes, precisamos lembrar de uma funçãozinha específica muito importante.
Função impulso
Provavelmente em algum momento da sua sofrida vida na faculdade você já viu em algum lugar a função impulso, também conhecida como Delta de Dirac. Se você não lembra (sem julgamentos, porque eu também não lembrava), vou refrescar a sua memória. A função Delta de Dirac, é definida da seguinte forma:
Ou seja, a função tem valor nulo para todos os valores de menos para onde ela assume o valor infinito.
Vamos imaginar uma função parecida, só que em vez de , em a função assumirá um valor unitário:
Dessa forma, ela teria a seguinte cara:
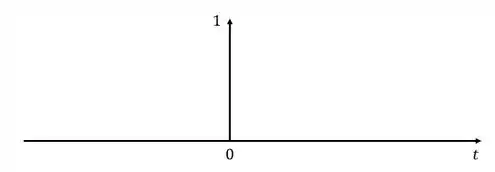
Vamos continuar brincando com esse conceito, se a gente deslocar esse impulso um pouco para a direita, teremos a seguinte função:
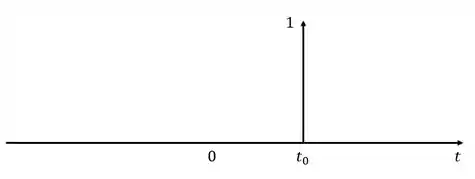
Lembra disso de cálculo? Quando a gente desloca uma função para a direita, nós subtraímos a quantidade deslocada do argumento da função.
Por último, vamos imaginar que a gente tem VÁRIOS impulsos afastados a uma quantidade de tempo contínua um do outro:
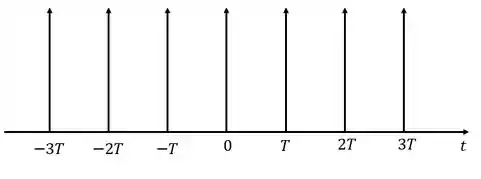
Se a gente fosse escrever essa função matematicamente, precisaríamos de um somatório, já que nela temos infinitas funções impulso juntas, sendo assim:
Repara que quando , teremos a função impulso em , quando teremos o impulso em , e assim por diante.
Essa última função, é chamada de trem de impulsos (hehe, esse nome é engraçado). Conseguiu entender como chegamos até ela? Vamos guardar essas conclusões na nossa manga rapidinho e daqui a pouco voltamos nela.
Amostragem
Beleza, vamos voltar agora para o nosso objetivo principal, que é fazer a amostragem de um sistema contínuo.
Vamos imaginar um sinal de entrada com a seguinte cara:
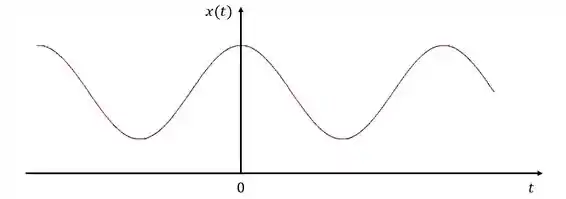
O que aconteceria se a gente multiplicasse essa função , pela função impulso?
Pensa comigo, a função impulso acima é para qualquer valor de , menos em onde é . Sendo assim, o produto das duas funções seria:
Da mesma forma, se eu multiplicasse a função pela função , eu obteria:
Ou seja, para conseguir o valor de uma função em um ponto específico, eu preciso multiplicar a minha função em tempo contínuo pelo impulso deslocado no tempo que eu preciso.
Se eu precisar de uma sequência de valores, ou, uma amostragem, basta que eu multiplique a minha função em tempo contínuo pela função trem de impulso. Como a função trem de impulso são vários impulsos afastados por um período (), o resultado dessa multiplicação, será a discretização da função , que chamaremos de :
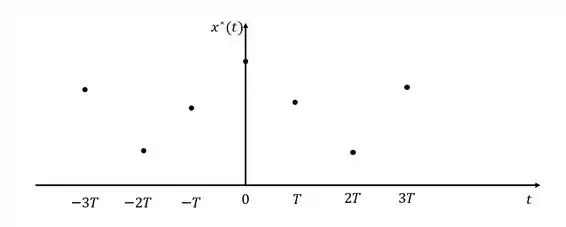
Ou seja, a função discretizada é a soma dos produtos entre a função no ponto e a função impulso deslocado para aquele ponto.
Retentor
Lá em cima, eu disse que para um controle digital funcionar é preciso converter um sinal analógico para um digital.
Quem faz essa conversão são os conversores A/D. Esses conversores são compostos geralmente por duas partes, o amostrador e o retentor (também chamado de hold).
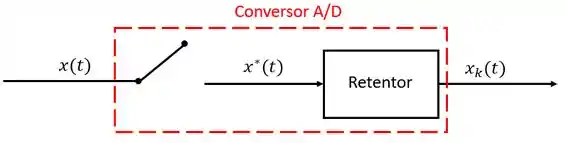
A função do amostrador, como já vimos, é fazer a discretização do sinal. Já o retentor, por sua vez, fará com que o sinal discretizado pelo amostrador seja mantido durante todo o período, , até que um novo sinal seja enviado quando a chave do amostrador fechar novamente.
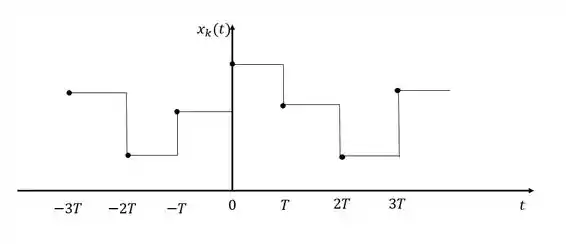
Depois que o sinal passa pelo retentor, dizemos que ele fica quantizado. Esse sinal discretizado e quantizado é o sinal que chamamos que chamamos de sinal digital.
A equação do retentor no domínio da frequência é dada abaixo:
O que essa função faz basicamente é segurar o valor que foi “fotografado” pelo amostrador por um tempo até que outra foto seja tirada e outro valor tenha que ser retido por um tempo .
Teorema da amostragem
Como acabamos de ver, para ser discretizado um sinal precisa ser “multiplicado” por um trem de impulso que tem um certo período de amostragem .
Esse período de amostragem também pode ser escrito na forma de frequência de amostragem, :
Para que a amostragem seja feita de maneira fiel ao sinal contínuo é necessário que a frequência de amostragem seja pelo menos duas vezes maior que a maior frequência presente no sinal contínuo no tempo.
Caso a frequência da amostragem seja menor que o dobro da frequência máxima contida no sinal contínuo, informações sobre o sinal serão perdidas e a reconstrução para o tempo contínuo não poderá ser feita com fidelidade e ocorre uma distorção no sinal chamado de efeito de aliasing.
Esse teorema é chamado de Teorema de Nyquist-Shannon ou simplesmente de Teorema da Abaixo, está representado um exemplo de uma amostragem que foi feita a uma frequência menor o dobro da frequência do sinal original.
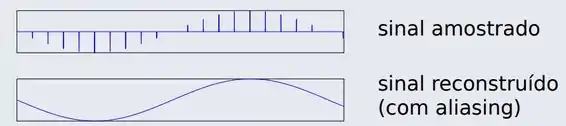
Repare que o sinal reconstruído é muito diferente do sinal original, essa distorção é o que chamamos de aliasing.
Se conhecemos a frequência máxima contida em um sinal, teremos a frequência mínima de amostragem para que não ocorra aliasing essa frequência é chamada de taxa de nyquist.
Caso a gente conheça a taxa de amostragem, conseguiremos identificar a frequência máxima que um sinal deve ter para que não ocorra aliasing, essa frequência é a frequência de nyquist.
Função impulso
Amostragem
Retentor
Teorema da amostragem
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Deseja-se montar um sistema de controle para controlar a temperatura de saída de uma corrente que sai de um aquecedor. Esse aquecedor é um trocador de calor que usa vapor de água para aquecer a corrente fria. Para efetuar esse controle serão usador um transmissor/sensor de temperatura e uma válvula que irá controlar a vazão de vapor de água que entra no trocador. Deseja-se realizar esse controle utilizando um controlador digital. Explique e represente no diagarama de blocos quais modificações deverão ser feitas na malha de controle para comportar o controlador digital. Explique como funciona as estruturas introduzidas para realizar a adaptação.
Passo 1
Em vez de ir direto ao ponto, vamos primeiro pensar como seria essa malha de controle caso o controlador fosse um analógico clássico.
Esse é aquele esquema clássico de controle feedback né. A temperatura de saída do trocador de calor é medida, no diagrama ela foi representada com , essa temperatura é então comparada com um valor de referência, , e gera o erro, . O controlador Recebe esse erro e decide o que fazer, mandando um sinal para a válvula que altera a variável controlada alterando o processo.
Passo 2
Entretanto, o nosso controlador que iremos usar é digital. Se você olhar o nosso diagrama de blocos, o controlador tá recebendo um sinal contínuo no tempo, ou seja, analógico. Sendo assim, precisaremos colocar uma estrutura de conversão de sinal no nosso diagrama de blocos para que o controlador digital possa funcionar.
Entretanto, apenas o controlador é digital, todos os outros instrumentos são analógicos, então após o controlador será preciso reconverter o sinal para o sinal analógico.
Vamos representar essas estruturas no diagrama de blocos então.
Sendo assim, acrescentamos um conversor analógico-digital antes do controlador e um conversor digital –analógico para voltar o sinal para o modo analógico após o controlador.
Passo 3
O conversor analógico-digital é formado por duas estruturas, uma que faz a amostragem do sinal, que é chamada de amostrador, e outra que quantiza esse sinal amostrado, ou seja, dá uma “segurada” no sinal até que uma nova amostra seja medida, que se chama retentor.
Sendo asism, o bloco do conversor A/D no diagrama de blocos poderia ser substituído por dois elementos:
A chavezinha do amostrador fecha em intervalos periódicos de tempo gerando o sinal amostrado enquanto o retentor tem segura o valor amostrado até que a chaveinha feche de novo.
Resposta
Exercício Resolvido #2
Elaboração própria.
Dado o sinal abaixo:
Represente esse sinal caso sofra uma amostragem com:
- O que pode-se concluir com os três resultados?
Passo 1
Caso o período seja iual a nós teremos um ponto da função discreta a cada unidades de tempo. Para o exemplo da questão, isso seria:
Passo 2
Agora vamos ver o que acontece quando reduzimos o período para 0,25 unidade de tempo:
Passo 3
E agora com o período de :
Passo 4
Com esse exemplo pode-se notar que quanto menor for o período de amostragem, mais o sinal discreto será parecido com o sinal contínuo
No priemeior caso, onde o período era todos os pontos tinham a mesma magnitude, dando a falsa impressão de que o sinal se tratava de uma constante.
Conforme fomos diminuindo o sinal, foi ficando cada vez mais fácil de reconhecer a função senoidal que de fato respresenta melhor o sinal contínuo.
Resposta
- Quanto menor o período de amostragem, melhor definido será o sinal discreto,
Exercício Resolvido #3
Elaboração própria.
Um dado sinal é composto por três tons senoidais de frequências , e . Determine a taxa de Nyquist.
Passo 1
A taxa de Nyquist é a menor taxa de amostragem possível para que não ocorra aliasing. Essa taxa é igual ao dobro da frequência máxima contida em um sinal:
Qunado isso acontece, nenhuma informação do sinal é perdida e ele poderá ser reconstituído posteriormente.
Passo 2
Sendo assim, para identificar a taxa de Nyquist devemos nos guiar pela maior frequência contida no sinal, que neste caso é . Portanto a taxa de Nyquist será:
Ou seja, precisaremos de uma taxa de amostragem de no mínimo para que não ocorra aliasing.
Resposta
Exercício Resolvido #4
Elaboração própria.
Um amostrador funciona com uma taxa de amostragem de . Dados os sinais abaixo, identifique aqueles que apresentarão aliasing quando amostrados por esse equipamento:
Passo 1
Vamos descobrir qual a frequência de Nyquist para esse amostrador. A frequência de Nyquist é metade da taxa de amostragem do amostrador. Portanto:
Passo 2
A frequência de Nyquist representa a maior frequência que um sinal deve ter para que não ocorra aliasing.
Sendo assim, nos itens a) e b) a frequência do sinal é menor que a frequência de Nyquist, portanto, o sinal não apresentará aliasing. Diferentemente do item c) onde a frequência é maior que a frequência de Nyquist e ocorrerá aliasing.
Resposta
- Não ocorrerá aliasing.
- Não ocorrerá aliasing.
- Ocorrerá aliasing.
Exercício Resolvido #5
Elaboração própria.
Dado o sinal abaixo:
Calcule a taxa de Nyquist.
Passo 1
Para calcular a taxa de Nyquist, precisamos saber a frequência do sinal. Para a função seno, a frequência é dada pelo argumento da função. Ou seja:
A frequência da função, em é igual a .
Para o nosso exercício teremos:
Passo 2
Como estamos em busca da taxa de Nyquist, essa medida é mais comumente dada em (amostras por segundo). Para fazer a mudança de unidade usaremos:
Onde é a frequência em e é a frequência em .
Vamos então encontrar a frequência do nosso sinal em :
Passo 3
Agora só falta encontrar a taxa de Nyquist.
A taxa de Nyquist é igual ao dobro da frequência máxima de um sinal. Como aqui só temos uma frequência, a taxa de Nyquist será:
Resposta
Exercício Resolvido #6
Elaboração própria.
Dado o sinal abaixo, calcule a taxa de Nyquist:
Passo 1
Para calcular a taxa de Nyquist devemos encontrar a maior frequência presente em um sinal. Como temos a soma de três parcelas, basta encontrar aquela que tem a maior frequência para determinar a taxa de Nyquist.
Como é uma constante, sua frequência é . Para as duas funções trigonométricas, basta ver aquela que tem o maior argumento que é a parcela .
Lembrando que a constante que multiplica as funções não interfere na frequência.
Passo 2
Vamos então encontrar a frequência de para conseguir determinar a taxa de Nyquist. Para a função cosseno, assim como para a função seno, a frequência é dada pelo argumento da função. Ou seja:
A frequência da função, em é igual a .
Para essa parcela teremos então:
Passo 3
Como estamos em busca da taxa de Nyquist, essa medida é mais comumente dada em (amostras por segundo). Para fazer a mudança de unidade usaremos:
Onde é a frequência em e é a frequência em .
Vamos então encontrar a frequência máxima do nosso sinal em :
Passo 4
Agora só falta encontrar a taxa de Nyquist.
A taxa de Nyquist é igual ao dobro da frequência máxima de um sinal. Como a frequência máxima foi a que encontramos anteriormente, teremos:
Resposta
Exercício Resolvido #7
Elaboração própria.
Calcule a taxa de Nyquist para os sinais abaixo:
Passo 1
Para calcular a taxa de Nyquist, precisamos saber a frequência do sinal. Para a função cosseno, assim como para a função seno, a frequência é dada pelo argumento da função. Ou seja:
A frequência da função, em é igual a .
Para a letra a) teremos então:
Passo 2
Como estamos em busca da taxa de Nyquist, essa medida é mais comumente dada em (amostras por segundo). Para fazer a mudança de unidade usaremos:
Onde é a frequência em e é a frequência em .
Vamos então encontrar a frequência do nosso sinal em :
Passo 3
Agora só falta encontrar a taxa de Nyquist.
A taxa de Nyquist é igual ao dobro da frequência máxima de um sinal. Como aqui só temos uma frequência, a taxa de Nyquist para a letra a) será:
Passo 4
Para o item b), podemos perceber que se trata da mesma função, porém multiplicado por uma constante.
A função cosseno quando multiplicada por uma constante não terá sua frequência alterada, apenas a sua magnitude. Os gráficos abaixo demonstram isso:
Os gráficos mostram os sinais da letra a) e b) respectivamente. Perceba que devido à multiplicação pela constante, a amplitude do sinal (tamanho dos picos e vales) dobrou, mas a frequência (quantidade de ciclos) num mesmo intervalo se manteve a mesma.
Portanto, a frequência do sinal não mudou e portanto a taxa de Nyquist para esse sinal também não mudará:
Passo 5
Para a letra c) teremos novamente o mesmo sinal, porém dessa vez, elevado ao quadrado.
Quando elevamos a função cosseno ao quadrado, toda a parte negativa dessa função será refletida para o eixo positivo:
Podemos perceber que quando comparamos o gráfico do sinal do item c) com o do item a) a frequência foi dobrada (dobrou a quantidade de ciclos), portantoa taxa de Nyquist também será dobrada:
Resposta
Exercício Resolvido #8
Elaboração própria.
Dado o sinal abaixo, qual seria a frequência do sinal discreto caso o sinal seja amostrado a uma taxa de .
Passo 1
Para resolver essa questão, vamos usar o gráfico do sinal para facilitar a visualização:
Perceba que o tempo que o sinal demora para completar um ciclo completo é de , fazendo com que a frequência seja de :
Esse valor é condizente com o valor que encontraríamos pela expressão do sina pois:
Passo 2
O sinal será amostrado a uma taxa de . O que quer dizer que a cada segundo, amostras serão colhidas.
Vamos determinar quanto tempo leva para colher cada amostra:
Ou seja, a cada segundos, uma amostra é feita.
Passo 3
Vamos fazer a amostragem usando o gráfico da função acima e uma amostra a cada segundos:
Passo 4
Repara que o ciclo começa em só se conclui em . Podemos calcular a frequência do sinal amostrado então:
Que é uma frequência oito vezes menor do que a frequência do sinal contínuo. Isso aconteceu porque a amostragem foi feita numa taxa menor que a taxa de Nyquist. Para esse caso a taxa de Nyquist seria:
Ou seja, qualquer amostragem que fosse feita a uma taxa superior a a frequência do sinal amostrado seria igual à do sinal contínuo. Como a taxa de amostragem foi menor, a frequência não foi a mesma. Isso é o que chamamos de aliasing.