Filtros digitais
Produzido por Alexandre NunesTeoria
Introdução
É muito comum em controle de processos, quando a gente recebe um sinal ser necessário selecionar especificamente a frequência que desejamos. Por exemplo, quando o médico está fazendo a ultrassonografia, ele deseja escutar o coração do bebê batendo para poder tranquilizar a futura mamãe de que está tudo bem com o bebê dela. Entretanto, o equipamento do médico capta um monte de ruído diferente que poderia atrapalhar o médico a ouvir o coração do bebê batendo. Nesse caso, o filtro tem a função de selecionar apenas o ruído com a frequência na faixa do ruído causado pelo batimento cardíaco do bebê, e amplifica-lo para que o médico possa ouvir com clareza.
Portanto, os filtros, como o próprio nome já diz, têm a função de filtrar um sinal fazendo com que as frequências desejadas passem e sejam amplificadas, e as frequências não desejadas sejam atenuadas. A faixa de frequência que o filtro deixa passar é chamada de banda de passagem enquanto a faixa de frequência que é barrada é chamada de banda de corte. A faixa intermediária entre essas duas bandas é chamada de banda de transição.
Existem uma série de filtros, dentre eles temos os filtros passa-baixa, onde as frequências mais baixas passam e as mais altas são atenuadas, os filtros passa-alta, onde as frequências altas passam e as frequências mais baixas são atenuadas. Os filtros passa-faixa aceitam apenas os sinais de uma faixa limitada de frequência, e os filtros rejeita-faixa rejeitam os sinais de uma faixa limitada de frequência.
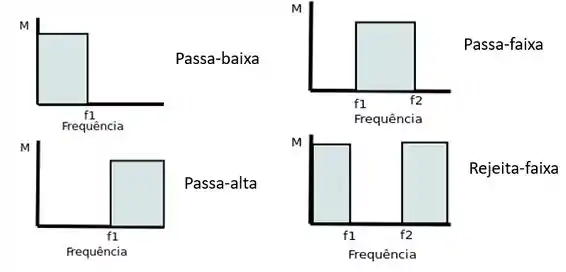
Os filtros na imagem acima são do tipo ideal. Isso significa que no valor exato da frequência de cote ocorre a mudança completa da banda de passagem para a banda de corte ou vice-versa. Um filtro real não se comporta dessa maneira, na realidade em valores próximos a frequência de corte começa a acontecer a transição entre as duas faixas criando-se assim uma banda de transição. A imagem abaixo representa um filtro real, nela é possível ver uma banda de passagem no inpicio, seguida de uma banda de transição e por última uma banda de rejeição.
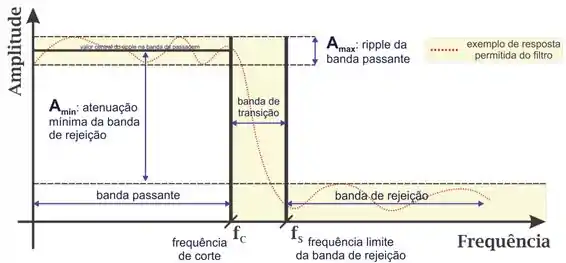
Perceba que o filtro do exemplo acima é um passa baixa, isso quer dizer que um sinal que passa por esse filtro terá a amplitude das baixas frequências grande (baixas frequências são amplificadas) e a amplitude das atas frequência serão pequenas (altas frequências são atenuadas). O ripple é a oscilação da banda de passagem, que no caso de cima, é a faixa de amplitude da banda de passagem.
Existem ainda alguns filtros, que tem a função de reduzir o ruído de um sinal, como é o caso dos filtros Butterworth e média móvel.
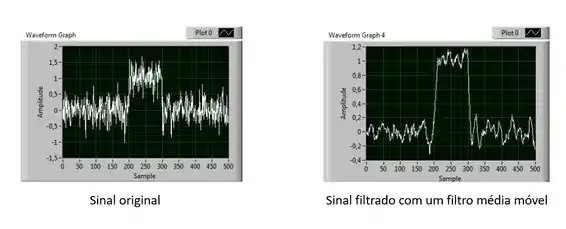
O sinal antes de passar pelo filtro era cheio de ruído todo estranho, depois que passa pelo filtro o ruído é reduzido, e o sinal fica mais “liso” digamos assim.
Filtros digitais
Um filtro digital opera um sinal matemático amostrado e quantizado, ao contrário do filtro analógico que opera um sinal contínuo no tempo.
Apesar de ser mais caro a implementação do filtro digital, ele é muito melhor em performance quando comparado com o filtro analógico.
Os filtros digitais são programáveis via software, são menos suscetíveis a variações no ambiente externo, tem melhor custo/benefício e não sofrem variação com o tempo. Todas essas são características que mostram a superioridade dos filtros digitais em relação aos filtros analógicos.
Os filtros digitais podem ser representados de três formas: resposta ao impulso, resposta ao degrau e resposta em frequência.
Essas três formas representam completamente as características de um filtro de forma independente, e, a partir de uma, é possível chegar às outras.
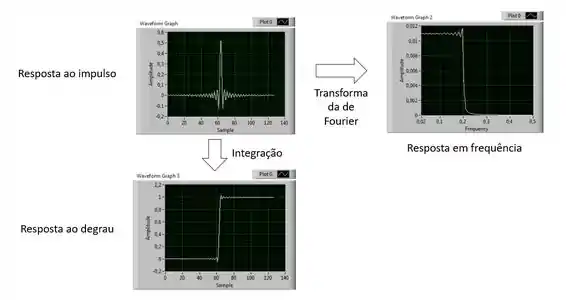
Através da integração da resposta ao impulso é possível chegar à resposta ao degrau. Aplicando transformada de Fourier na resposta ao impulso, é possível chegar à resposta em frequência.
A resposta em frequência também pode ser representada em decibéis igual a gente fazia quando trabalhava com diagrama de Bode, lembra? Para fazer a transição da escala linear para decibeis, basta aplicar em toda a transformada de Fourier. Essa mudança de escala é muito utilizada pois facilita a visualização do gráfico da resposta em frequência que geralmente apresenta grandes variações em curtos intervalos de frequência.
Os filtros digitais, podem ser implementados de duas formas: por convolução ou por recursão.
Os filtros por convolução, também são chamados de FIR (filtro de resposta finita ao impulso). Esses filtros são implementados por convolução da resposta de impulso. Geralmente eles têm ótima performance, mas podem ser bem lentos. O filtro de média móvel é um clássico exemplo de filtro FIR. Os filtros FIR são sempre estáveis, isto acontece porque eles não usam realimentação, isto é, não precisam da sua própria saída como entrada.
Já os filtros IIR (filtro de resposta ao impulso infinito) são implementados de forma recursiva, o que implica que a saída do filtro em um certo momento, depende de saídas anteriores. Eles geralmente têm um desempenho levemente inferior aos filtros FIR, mas são mais rápidos. Diferentemente dos filtros FIR, os filtros IIR podem se tornar instáveis.
Transformação de filtros analógicos em filtros digitais
Os filtros analógicos são relacionados aos filtros digitais IIR, pois ambos apresentam características recursivas. Sendo assim, é possível transformar um filtro analógico passa-baixa bem conhecido em um filtro digital IIR.
Antes de falar sobre a técnica da transformação em si, vamos fazer uma diferenciação entre dois tipos de frequência que usaremos daqui para frente.
é a frequência em tempo discreto, enquanto é a frequência em tempo contínuo. Ou seja, quando estivermos trabalhando com filtros analógicos, usaremos , e com filtros digitais .
Beleza, dito isso, vamos voltar para o nosso objetivo que é transformar um filtro analógico passa-baixa em um filtro digital e para isso, uma das técnicas que pode ser usada é a técnica da transformação bilinear.
Essa técnica consiste em mapear a função de transferência de um filtro passa-baixa bem conhecida entre o plano e o plano .
Esse mapeamento é feito através da seguinte transformação:
Essa equação é a chamada transformação bilinear e ela mapeia o semiplano esquerdo dentro de um círculo de raio unitário no plano , o eixo é mapeado como o raio desse círculo e o semiplano direito é mapeado no exterior do círculo de raio 1 no plano .
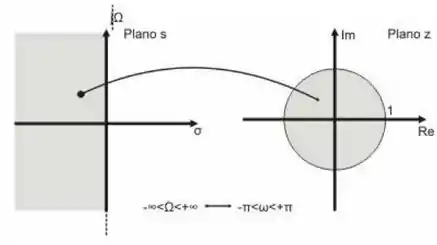
Através dessa transformação, as frequências em tempo discreto e em tempo contínuo passam a ter a seguinte relação:
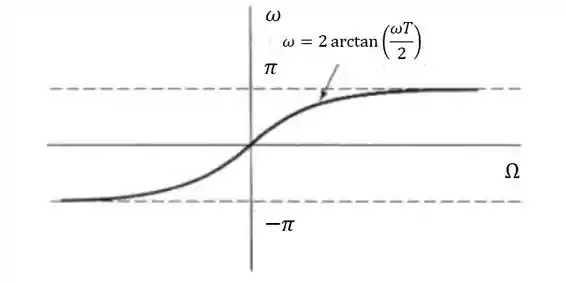
Através do gráfico podemos perceber que quando variamos a frequência no tempo contínuo de até a frequência em tempo discreto varia de a . Isso acontece porque como na transformação bilinear o eixo dos reais é mapeado como a circunferência de raio unitário, tanto quanto são mapeado em , cujo ângulo de fase é ou dependendo do sentido em que se olha.
Sendo assim, se tivermos o filtro analógico:
E quiséssemos transformar ele em um filtro digital com período de amostragem , faríamos a seguinte mudança de variáveis:
Multiplicando por em cima e embaixo:
Filtros digitais
Transformação de filtros analógicos em filtros digitais
Exercícios Resolvidos
Exercício Resolvido #1
COMPERVE – 2011 – UFRN – Físico. Adaptado.
Considere as afirmativas acerca de filtros digitais:
- Um filtro FIR utiliza apenas o sinal de entrada.
- Um filtro IIR utiliza tanto o sinal de entrada quanto o sinal de saída
- Um filtro IIR são sepre estáveis, enquanto os filtros FIR podem ser instáveis.
Estão corretas as afirmativas:
- Apenas II e III
- Apenas I e II
- Apenas I e III
- I, II e III
Passo 1
A primeira afirmativa diz que os filtros FIR utilizam apenas o sinal de entrada.
Esse tipo de filtro é implementado através de convolução da resposta ao impulso e não utilizam o sinal de saída como entrada, sendo assim, a afirmativa está correta.
Passo 2
Os filtros IIR por sua vez sempre utilizarão o sinal se saída como entrada, por isso dizemos que eles são implementados de forma recursiva. Portanto a segunda afirmativa tabém é verdadeira.
Passo 3
A última afirmativa diz que os fitros IIR são sempre estáveis enquanto os FIR podem ser instáveis.
Na verdade, é justamente o contrário, como os filtros FIR não usam a própria saída como entrada, eles são sempre estáveis enquanto os filtros IIR podem ser instáveis. Em compensação, os filtros IIR são mais rápidos.
Portanto, a terceira afirmativa é falsa.
Resposta
- Apenas I e II
Exercício Resolvido #2
CESPE - 2013 - INPI - Analista de Planejamento - Engenharia Elétrica
A equação abaixo corresponde a um filtro FIR ou IIR?
Passo 1
A pergunta da questão é bem direta, mas antes de responde-la vamos relembrar os conceitos de filtro FIR e IIR.
Os filtros FIR (finite impulse response) são implementados por convolução ao impulso e jamais utilizam a própria saída como entrada. Já os filtros IIR (infinite impulse response) são implementados de forma recursiva, ou seja, eles necessitam da saída do filtro em momentos anteriores para funcionar. Os fitros IIR geralmente são mais rápidos, entretanto, os filtros FIR têm um desempenho melhor e jamais se tornam instáveis.
Passo 2
Sendo assim, a principal coisa que devemos obeservar aqui é se o filtro depende ou não da sua própria saída.
Nesse caso, a saída depende apenas do sinal de entrada, , e do sinal de entrada em momentos anteriores, e .
Portanto, a saída não depende da própria saída, e o filtro portanto é do tipo FIR.
Resposta
Filtro FIR.
Exercício Resolvido #3
Engenharia Elétrica - Processamento Digital de Sinais - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2012 - INPI - Analista de Gestão
Considere que as entradas de filtros digitais sejam representadas por x[n] e que as saídas sejam representadas por y[n]. Com base nessas informações e nos conceitos relacionados a filtros digitais, julge a afirmativa abaixo.
A equação
Corresponde a um filtro digital do tipo IIR.
Passo 1
A pergunta da questão é bem direta, mas antes de responde-la vamos relembrar os conceitos de filtro FIR e IIR.
Os filtros FIR (finite impulse response) são implementados por convolução ao impulso e jamais utilizam a própria saída como entrada. Já os filtros IIR (infinite impulse response) são implementados de forma recursiva, ou seja, eles necessitam da saída do filtro em momentos anteriores para funcionar. Os fitros IIR geralmente são mais rápidos, entretanto, os filtros FIR têm um desempenho melhor e jamais se tornam instáveis.
Passo 2
Portanto, para a equação respresentar um filtro IIR, a saída precisa estar e função da própria saída. Vamos isolar para ficar mais fácil de ver:
Pela equação podemos ver que o sinal de saída além das entradas, , e também depende do próprio sinal de saída em momentos anteriores e . Por isso, dizemos que o filtro é um filtro implementado de forma recursiva, e portanto, um filtro IIR.
Resposta
A afirmativa está correta, o fitro é do tipo IIR.
Exercício Resolvido #4
Engenharia Elétrica - Processamento Digital de Sinais - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2014 - TJSE/SE - Analista Judiciário
Acerca de processamento de sinais, julgue os itens que se seguem. No processo de aquisição de um sinal analógico, o filtro anti-aliasing é ajustado para a seletividade de frequência do tipo passa-baixa. Avalie se a afirmação está correta ou errada.
Passo 1
Para responder essa questão nós precisamos entender dois conceitos: aliasing e filtros passa-baixa.
Vamos então relembrar o que é aliasing.
Aliasing é um efeito que pode distorcer um sinal durante o processo de reconstituição de um sinal analógico após ele ser amostradado. O aliaising acontece quando o sinal é amostrado a uma taxa muito baixa. Para garantir que o aliasing não aconteça é necessário que a taxa de amostragem seja pelo menos o dobro da maior frequência contida no sinal. Essa taxa é chamada de taxa de Nyquist, enquanto a frequência que é igual à metade da taxa de Nyquist é chamada de frequência de Nyquist.
Passo 2
Os filtros passa-baixa são os filtros que permitem a passagem de frequências baixas e impedem que frequências altas passem.
Sendo assim, ele terá uma certa frequência de corte, se ele for um filtro ideal, qualquer frequência acima da frequência de corte será anulada e só passarão sinais com frequência menor que a frequência de corte.
Passo 3
Sendo assim, uma consequência que acontece quando usamos um filtro passa-baixa é que ele diminui a frequência máxima presente no sina. Como ele “corta” frequências muito altas, a maior frequência presente no sinal será a frequência de corte, fazendo com que a taxa de Nyquist diminua e tornando mais fácil impedir o aliasing.
Portanto, a afirmativa é verdadeira.
Resposta
A afirmativa está correta.
Exercício Resolvido #5
Elaboração própria
Um dos diagramas abaixo representa a estrutura de um filtro do tipo IIR e outro de um filtro FIR. Diga qual é cada um e justifique sua resposta.
Passo 1
Para responder essa questão, precisaremos lembrar da principal distinção de um filtro FIR para um IIR.
Os filtros FIR não dependem do sinal de saída, enquanto os filtros IIR dependem.
Sendo assim, se olharmos ao primeiro diagrama veremos que a saída depende apenas de sinais de entrada , seja no presente ou no passado. Em nenhum momento é adicionado ao sistema um sinal de saída . Sendo assim, se fôssemos escrever agebricamente esse sinal. Seria algo como:
Portanto, o primeiro diagrama é do tipo FIR.
Passo 2
Já no segundo diagrama, o sinal de saída depende dos sinais de saída anteriores, apresentand portanto uma característica recursiva.
Poderíamos escrever ele como:
Os fitros que apresentam carcaterística recursiva são os filros IIR.
Resposta
- Fitro FIR
- Filtro IIR
Exercício Resolvido #6
Elaboração própria
Dado o filtro analógico passa-baixa Butterworth de primeira ordem com frequência de corte mostrado abaixo:
Encontre a função de transferência dos filtros digitais passa-baixas com frequência de corte .
Passo 1
O exercício quer que a gente pegue a função de transferência do filtro passa-baixa analógico com frequência de corte e o transforme em um filtro digital com frequência de corte .
Isso quer dizer que no mundo digital o nosso filtro começa a cortar, isto é, atenuar o sinal, a partir da frequência , enquanto no mundo digital, nosso objetivo é que ele faça isso a partir da frequência .
Passo 2
Para mudar a frequência de corte, nós precisaremos de um período de amostragem específico para fazer essa transformação.
Para encontrar esse período de amostragem, utilizaremos a seguinte fórmula:
Se isolarmos o período de amostragem, teremos:
Como temos:
O período será:
Passo 3
Agora que temos o período de amostragem, só precisamos aplicar a transformação bilinear para conseguir o filtro digital.
A transformação bilinear que usaremos é:
Como:
Teremos:
Substituindo na função de transferência, teremos:
Rearranjando:
Resposta
Exercício Resolvido #7
Elaboração própria
Dado o filtro analógico passa-baixa Butterworth de segunda ordem com frequência de corte mostrado abaixo:
Encontre a função de transferência do filtro digitais passa-baixa com frequência de corte .
Passo 1
O exercício quer que a gente pegue a função de transferência do filtro passa-baixa analógico com frequência de corte e o transforme em um filtro digital com frequência de corte .
Isso quer dizer que no mundo digital o nosso filtro começa a cortar, isto é, atenuar o sinal, a partir da frequência , enquanto no mundo digital, nosso objetivo é que ele faça isso a partir da frequência .
Passo 2
Para mudar a frequência de corte, nós precisaremos de um período de amostragem específico para fazer essa transformação.
Para encontrar esse período de amostragem, utilizaremos a seguinte fórmula:
Se isolarmos o período de amostragem, teremos:
Como temos:
O período será:
Passo 3
Agora que temos o período de amostragem, só precisamos aplicar a transformação bilinear para conseguir o filtro digital.
A transformação bilinear que usaremos é:
Como:
Teremos:
Substituindo na função de transferência, teremos:
Multiplicando em cima e embaixo por , teremos:
Essa última forma já é suficiente como resposta.
Resposta
Exercício Resolvido #8
Vinkay K. Ingle, Digital Signal Processing Using Matlab, Exemplo 8.15
Transforme em um filtro digital usando a transformação bilinear. Escolha .
Passo 1
Como já foi dado a função de transferência e o período desejado, nossa missão aqui é razoavelmente simples.
Precisamos aplicar a transformação abaixo:
Com:
Na função de transferência:
Obtendo assim, .
Passo 2
Como , a transformação sera:
Substituindo em , teremos:
Para simplificar, vamos multiplicar por em cima e embaixo:
Por fim: