Sistemas discretos no tempo
Produzido por Alexandre NunesTeoria
Sistemas contínuos vs Sistemas discretos
Até aqui, viemos estudando o controle de processos utilizando sistemas contínuos no tempo.
Sistemas contínuos no tempo são aqueles sistemas que dada uma entrada contínua obtemos uma saída também contínua.
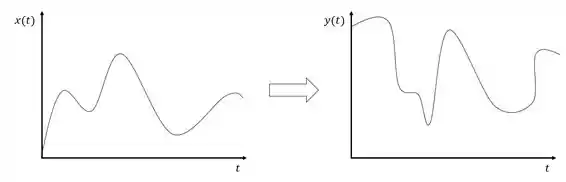
Ou seja, dada uma função de entrada contínua , o sistema resultada uma função de saída contínua .
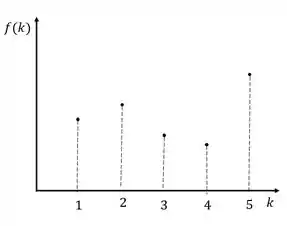
Um sistema é discreto quanto transforma entradas em tempo discreto em saídas de tempo discreto. Uma entrada em tempo discreto são entradas pontuais. A função abaixo é um exemplo de função discreta no tempo.
Um circuito é um exemplo de um sistema contínuo no tempo.
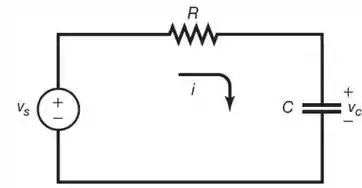
Para esse circuito, a modelagem em tempo contínuo nos dá:
Vamos agora tentar pensar num exemplo de sistema discreto.
Imagina que você dá aulas particulares e todo mês recebe uma quantidade de dinheiro diferente. Desse dinheiro que você recebe você sempre separa metade para investir em cursos para sua formação e para pagar a Netflix. O restante você guarda porque você quer comprar um computador novo porque o seu já tá no bico do urubu. Vamos tentar montar uma equação que nos dê o quanto você tem a cada mês.
é um mês qualquer;
é o quanto você recebeu em um mês k;
é o dinheiro que você tem no mês .
Sendo assim, a nossa equação ficará:
Ou seja, a quantidade de dinheiro que você tem em um mês é igual ao que você tinha guardado do mês anterior mais o seu salário do mês atual descontado o que você separa para sua formação e para Netflix.
Esse sistema é discreto porque as entradas não são contínuas, elas são pontuais a cada mês e produz saídas pontuais.
Os sistemas discretos, assim como os sistemas contínuos, podem ser classificados de diversas maneiras, e são essas classificações que veremos abaixo.
Sistemas com e sem memória
Os sistemas discretos podem ser do tipo com memória ou sem memória.
Um sistema com memória é um sistema cuja saída em um dado instante depende de saídas anteriores. O sistema do exemplo anterior é um sistema com memória
Nesse sistema, a quantidade de dinheiro que você tem no mês depende da quantidade de dinheiro que você tinha no mês anterior (), e por isso esse sistema é classificado como “com memória”.
Outro exemplo de sistema “com memória” é a sequência de Fibonacci. Na sequência de Fibonacci, cada termo é igual à soma dos dois termos anteriores. Sendo assim:
Um sistema sem memória, por sua vez, independe de qualquer valor anterior só importando os valores de entradas e saídas do instante atual. Por exemplo, o lucro líquido de uma empresa em um determinado mês :
O lucro no mês , , é igual à receita nesse mês, , menos os gastos nesse mês, .
Sistemas invertíveis
Um sistema é chamado de invertível quando para cada entrada diferente, obtém-se uma saída diferente.
Basicamente, um sistema pode ser considerado invertível se existir algum sistema inverso que você pode aplicar à resposta do seu sistema original e obter a mesma entrada.

Um exemplo prático seria com o sistema acumulador. O sistema acumulador é um sistema que soma todos os termos de entrada anteriores:
O sistema acumulador, também pode ser escrito da seguinte maneira:
Como o valor anterior da variável compreende a soma de todas as entradas até , para obter o valor de basta somar com a entrada atual, .
Sendo assim, o inverso desse sistema é dado pela expressão abaixo:
Os sistemas não-invertíveis são aqueles onde não existem sistemas que conseguem reverter todas as saídas de volta à suas entradas originais. Exemplo:
Esse sistema não é invertível pois para valores diferentes de são encontradas o mesmo valor de .
Causalidade
A gente diz que um sistema é causal quando a saída em qualquer instante depende apenas das entradas presentes ou das anteriores.
Qualquer sistema que tenha algum termo antecipativo é um sistema não-causal.
Esse sistema é não-causal. O termo adiciona um aspecto antecipativo ao sistema eliminando sua causalidade.
Invariância e linearidade
Para um sistema ser invariante, um deslocamento de tempo na entrada faz com que a saída sofra o mesmo deslocamento de tempo.
Imagine que a saída, , seja uma função da entrada :
Para um sistema ser invariante no tempo é preciso que:
Para um sistema ser considerado linear ele deve atender ao critério da homogeneidade:
O critério da homogeneidade diz que se uma dada entrada resulta em uma saída , se multiplicarmos essa entrada por uma constante, a saída deverá ser multiplicada pela mesma constate.
Ele também deve atender ao critério da aditividade:
Ou seja, se uma entrada gera uma saída , e uma entrada gera uma saída , uma entrada que seja a soma dessas duas entradas produzirá uma saída que será a soma das duas saídas anteriores.
Escrevendo o matematiquês de outra forma:
Se o sistema for linear, nós podemos escrever a saída como a soma das funções das duas entradas separadamente.
Além disso, poderemos também dizer que a função de uma constante vezes a entrada é igual à constante vezes a função da entrada, ou seja, podemos colocar a constante de multiplica a entrada para fora.
Estabilidade
Para terminar a última propriedade que veremos dos sistemas discretos no tempo é a propriedade da estabilidade.
Para que um sistema seja considerado estável é preciso que ele gere respostas limitadas para entradas limitados.
É o que chamamos de critério BIBO (Bound Input, Bound Output), que significa exatamente isso: entrada limitada, saída limitada.
Em resumo, para um sistema ser estável ele deve produzir uma resposta que não tenda ao infinito para qualquer entrada que não seja infinito.
Ou seja, se a entrada de um sistema for uma constante (ex: , , ) para ele ser estável a saída do sistema não pode tender ao infinito.
Se, o único momento que um sistema tende ao infinito é quando sua entrada tende ao infinito, o sistema é considerado então estável