Estabilidade de sistemas discretos
Produzido por Alexandre NunesTeoria
Introdução
A estabilidade é um tópico muito importante no estudo de controle de processos. Quando estávamos estudando o controle analógico nós vimos várias técnicas para determinar a estabilidade de um sistema.
No controle analógico, o critério de estabilidade dizia que para o sistema ser estável, todos os polos da função de transferência em malha fechada deveriam se encontrar no semiplano esquerdo do plano .
Por exemplo, para o diagrama de blocos feedback mostrado abaixo:
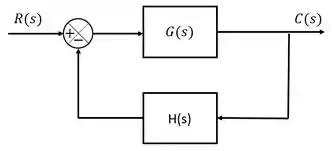
A função de transferência será:
Sendo assim, para determinar a estabilidade dessa malha, precisaríamos analisar a equação característica, que é o denominador da função de transferência:
As raízes dessa equação característica devem ter a parte real negativa para que o sistema seja estável.
Entretanto, quando estamos trabalhando com sistemas discretizados como o mostrado abaixo teremos que considerar um outro fator.
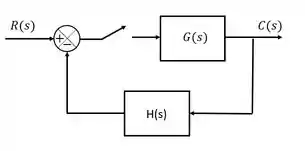
O amostrador inclui um outro parâmetro no nosso sistema que é o tempo de amostragem. O tempo de amostragem impacta diretamente a estabilidade do sistema discreto e se estiver fora de uma faixa estipulada pode leva-lo à instabilidade.
Vamos ver então como fazer a análise de estabilidade em sistemas digitais e quais critérios usaremos.
Critério de estabilidade no plano z
Para analisar a estabilidade de sistemas digitais, também precisaremos analisar as raízes da equação característica do sistema, porém dessa vez, estaremos trabalhando no plano z e o critério será um pouquinho diferente.
Pela definição da variável , temos que:
Se fizermos teremos:
Podemos aplicar a identidade de Euler na equação acima:
A partir dessa equação é possível mapear todo o plano no plano .
Quando esse mapeamento é feito percebemos um resultado bastante interessante que pode ser visto na figura abaixo.
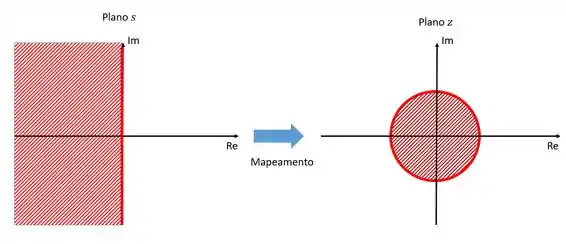
Todo o semiplano esquerdo do plano é mapeado para o interior de uma cisrcunferência de raio no plano . O eixo imaginário, , no plano se torna pontos no plano com módulo , ou seja, a extremidade da circunferência. Qualquer ponto no semiplano direito do plano acaba sendo mapeado no exterior da circunferência de raio no plano .
Dessa forma, precisamos adaptar nosso critério de estabilidade. Se quando estávamos trabalhando com sistemas contínuos (domínio ), o sistema era estável se todas as raízes de sua equação característica se encontrassem no semiplano esquerdo do plano , quando estivermos trabalhando com sistemas discretos (domínio ), o sistema será estável somente se todas as raízes de sua equação característica se encontrar no interior da circunferência de raio unitário e centro na origem.
Ou seja, retomando o exemplo da introdução:
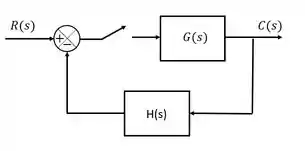
A função de transferência no domínio será:
Ou seja, a equação característica será:
Para o sistema ser estável, é preciso que todas as raízes dessa equação se encontrem no interior do semicírculo de raio unitário e centro na origem, ou seja, as raízes devem ter módulo menor que .
Trabalhando no plano s
Quando a gente estava trabalhando com sistemas de tempo contínuo e a equação característica da função de transferência era de ordem muito elevada, nós tínhamos ferramentas a mãos para conseguir driblar esse problema. O critério de Routh-Hurwitz era uma dessas ferramentas.
Com esse critério, era possível determinar quantas raízes se encontravam no semiplano direito sem saber exatamente quais eram as raízes.
Com sistemas de tempo discreto, essa ferramenta não é mais útil, uma vez que o critério é outro completamente diferente. Então como faremos quando o grau da nossa equação característica for muito grande?

Bom, quando isso acontecer, a gente pode usar um truquezinho para voltar a função de transferência para o domínio e então aplicar os métodos que a gente já estudou para sistemas contínuos para determinar a estabilidade do sistema discreto.
Esse truquezinho atende pelo nome de transformação bilinear. Basicamente o que faremos será aplicar a transformação abaixo na nossa equação característica que se encontra no domínio :
Quando fizermos essa substituição, a equação característica do sistema discreto que antes estava no domínio passará para o domínio . Após fazermos isso, só precisamos aplicar o critério de Routh-Hurwitz e ver se a equação possui ou não raízes no semiplano direito.
Obs: Se você não lembra desse critério seria legal dar uma revisada nas aulas de estabilidade e de critério de Routh- Hurwitz.
Critério de estabilidade no plano z
Trabalhando no plano s
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 13.6
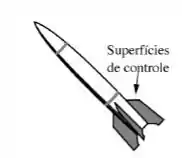
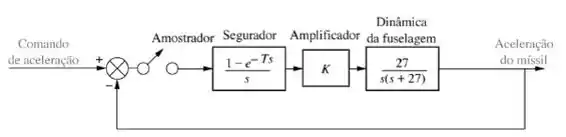
O míssil mostrado na figura abaixo pode ser controlado aerodinamicamente através de torques gerados pela deflexão de superfícies de controle no corpo do míssil. Os comandos para defletir essas superfícies de controle vêm de um computador que utiliza dados de rastreamento em conjunto com equações de guiamento programadas paradeterminar se o míssil segue a trajetória. As informações provenientes das equações de guiamento são utilizadas para desenvolver comandos de controle de voo para o míssil. Um modelo simplificado é mostrado abaixo. Nesse caso o computador executa a função de controlador utilizandoas informações de rastreamento para desenvolver comandos de entrada para o míssil. Um acelerômetro no míssil detecta a aceleração real, a qual é realimentada para o computador. Obtenha a função de transferência digital em malha fechada para esse sistema e determine se o sistema é estável para período de amostragem .
Passo 1
Para determinar a estabilidade do sistema digital primeiro devemos encontrar a função de transferência em malha fechada dele no plano . Para isso, não podemos encontrar a função de transferência no plano e depois aplicar a transformada .
A abordagem correta na verdade é encontrar a função de transferência em malha aberta no plano , aplicar a transformada , encontrando a função de transferência em malha aberta no plano e com ela encontrar a função de transferência em malha dechada no plano .
Então vamos lá, primeiro de tudo vamos achara a função de transferência em malha aberta no plano :
Passo 2
Agora aplicamos a transformada para encontrar :
O ganho como é uma constante pode vir pra fora da transformada:
Manipulando um pouco temos:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 3
Para fazer a transformada vamos aplicar a divisão em frações parciais:
Olhando uma tabela de transformada teremos:
Portanto:
Simplificando:
Faznedo o MMC e juntando tudo:
Botando em evidência na segunda parte:
Substituindo:
Passo 4
Com a função de transferência em malha abreta podemos encontrar a função de transferência em malha fechada, :
Portanto:
Multplicando em cima e embaixo por teremos:
Passo 5
Agora que finalmente temos a função de transferência em malha fechada e no domínio , podemos determinar a estabilidade. Para isso precisamos olhar para a equação característica da função de transferência, isto é, o polinômio do denominador:
Expandindo a equação característica:
Para que o sistema seja estável, as raízes dessa equação devem pertencer ao ciclo unitário, ou seja, (ter módulo menor que 1).
Como é um polinômio de segunda ordem, vamos aplicar Bhaskara:
Para saber se essas raízes estão dentro do círculo unitário, basta extrair o módulo delas:
Como o módulo é menor que , as raízes se encontrar dentro do círculo de raio unitário e o sistema é estável.
Resposta
Sistema estável.
Exercício Resolvido #2
Elaboração própria
Determine se o sistema discreto abaixo é estável:
Passo 1
Para que um sistema discreto seja estável, as raízes de sua equação característica no domínio devem estar dentro do círculo de raio unitário e com centro na origem. Em outras pealavras, o módulo das raízes deve ser menor que .
A equação característica nada mias é do que o denominador da função de transferência em malha fechada, como o exercício já nos deu a expressaõ da função de transferência em malha fechada, a equação característica será:
Passo 2
Aplicando Bhaskara para encontrar as raízes da equação:
Para saber se essa raíz se encontra ou não dentro do cícrculo de raio unitário com centro na origem, vamos calcular seu módulo:
Como o módulo das raízes é menor que , elas se encontram dentro do círculo, e portanto, o sistema é estável.
Resposta
Sistema estável.
Exercício Resolvido #3
Elaboração própria
Dado o sistema abaixo, encontra a faixa para o tempo de amostragem que torna o sistema estável:
Passo 1
Para que um sistema discreto seja estável, as raízes de sua equação característica no domínio devem estar dentro do círculo de raio unitário e com centro na origem. Em outras pealavras, o módulo das raízes deve ser menor que .
A equação característica nada mias é do que o denominador da função de transferência em malha fechada, como o exercício já nos deu a expressaõ da função de transferência em malha fechada, a equação característica será:
Passo 2
Como a equação característica é uma equação do segundo grau, ela terá duas raízes. Uma delas é:
E como:
Essa raíz satisfaz ao critério de estabilida, pois está dentro do círculo de raio unitário.
Passo 3
A segunda raíz será:
Para que o sistema seja estável essa raíz também deve atender ao critério de estabilidade, ou seja:
Sendo assim, vamos encontrar os valores de que fazem com que a raíz seja igual a e para determinar a faixa de .
Passo 4
Primeiro vamos achar o valor de que torna a raíz igual a :
Aplicando logaritmo em ambos os lados:
Passo 5
Agora vamos encontrar o valor de que faz com que a raíz seja :
Aplicando logaritmo em ambos os lados:
Portanto a faixa aceitável para o período de amostragem é:
Resposta
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 13.7
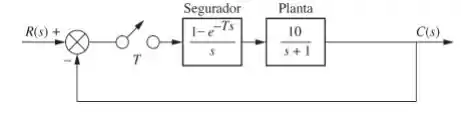
Determine a faixa de período de amostragem, , que tornará o sistema mostrado abaixo estável, e a faixa que o tornará instável.
Passo 1
Para determinar a estabilidade do sistema digital primeiro devemos encontrar a função de transferência em malha fechada dele no plano . Para isso, não podemos encontrar a função de transferência no plano e depois aplicar a transformada .
A abordagem correta na verdade é encontrar a função de transferência em malha aberta no plano , aplicar a transformada , encontrando a função de transferência em malha aberta no plano e com ela encontrar a função de transferência em malha dechada no plano .
Então vamos lá, primeiro de tudo vamos achara a função de transferência em malha aberta no plano :
Passo 2
Agora aplicamos a transformada para encontrar :
Manipulando um pouco temos:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 3
Para fazer a transformada vamos aplicar a divisão em frações parciais:
Olhando uma tabela de transformada teremos:
Portanto:
Simplificando:
Fazendo o MMC e juntando tudo:
Passo 4
Com a função de transferência em malha abreta podemos encontrar a função de transferência em malha fechada, :
Portanto:
Multplicando em cima e embaixo por teremos:
Passo 5
Para que o sistema seja estável, as raízes da equação característica devem estar dentro da circunferência de raio unitário com centro na origem. A equação característica para o sistema é o denominador da função de transferência, portanto:
Como é um polinômio de primeira ordem, terá apenas uma raiz, que será:
Ou seja, para que o sistema seja estável é necessário que:
Passo 6
Vamos primeiro encontrar o valor de que torna a raíz :
Aplicando logaritmo em ambos os lados:
E agora, vamos ber qual valor de faz com que a raíz seja :
Aplicando logaritmo em ambos os lados:
Resposta
Portanto o sistemas é estável em e instável em .
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 13.5
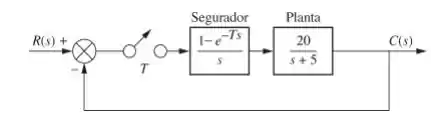
Determine a faixa de período de amostragem, , que tornará o sistema mostrado abaixo estável.
Passo 1
Para determinar a estabilidade do sistema digital primeiro devemos encontrar a função de transferência em malha fechada dele no plano . Para isso, não podemos encontrar a função de transferência no plano e depois aplicar a transformada .
A abordagem correta na verdade é encontrar a função de transferência em malha aberta no plano , aplicar a transformada , encontrando a função de transferência em malha aberta no plano e com ela encontrar a função de transferência em malha dechada no plano .
Então vamos lá, primeiro de tudo vamos achara a função de transferência em malha aberta no plano :
Passo 2
Agora aplicamos a transformada para encontrar :
Manipulando um pouco temos:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 3
Para fazer a transformada vamos aplicar a divisão em frações parciais:
Olhando uma tabela de transformada teremos:
Portanto:
Simplificando:
Fazendo o MMC e juntando tudo:
Passo 4
Com a função de transferência em malha abreta podemos encontrar a função de transferência em malha fechada, :
Portanto:
Multplicando em cima e embaixo por teremos:
Passo 5
Para que o sistema seja estável, as raízes da equação característica devem estar dentro da circunferência de raio unitário com centro na origem. A equação característica para o sistema é o denominador da função de transferência, portanto:
Como é um polinômio de primeira ordem, terá apenas uma raiz, que será:
Ou seja, para que o sistema seja estável é necessário que:
Passo 6
Vamos primeiro encontrar o valor de que torna a raíz :
Aplicando logaritmo em ambos os lados:
E agora, vamos ber qual valor de faz com que a raíz seja :
Aplicando logaritmo em ambos os lados:
Resposta
Portanto o sistemas é estável em e instável em .
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 13.14. Adaptado
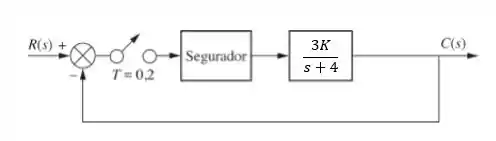
Determine a faixa de ganho, , para tornar o sistema mostrado na figura abaixo estável.
Passo 1
Para determinar a estabilidade do sistema digital primeiro devemos encontrar a função de transferência em malha fechada dele no plano . Para isso, não podemos encontrar a função de transferência no plano e depois aplicar a transformada .
A abordagem correta na verdade é encontrar a função de transferência em malha aberta no plano , aplicar a transformada , encontrando a função de transferência em malha aberta no plano e com ela encontrar a função de transferência em malha dechada no plano .
Então vamos lá, primeiro de tudo vamos achara a função de transferência em malha aberta no plano :
Onde é a função de transferência do segurador.
Passo 2
Agora aplicamos a transformada para encontrar :
Manipulando um pouco temos:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 3
Para fazer a transformada vamos aplicar a divisão em frações parciais:
Olhando uma tabela de transformada teremos:
Portanto:
Simplificando:
Fazendo o MMC e juntando tudo:
Sunstituindo :
Passo 4
Com a função de transferência em malha abreta podemos encontrar a função de transferência em malha fechada, :
Portanto:
Multplicando em cima e embaixo por teremos:
Passo 5
Para que o sistema seja estável, as raízes da equação característica devem estar dentro da circunferência de raio unitário com centro na origem. A equação característica para o sistema é o denominador da função de transferência, portanto:
Como o nosso polinômio é de primeira ordem, nós teremos apenas uma raíz. Para o sistema ser estável, é necessário que essa raíz esteja compreendida entre e .
A razíz será então:
Passo 6
Vamos primeiro encontrar o valor de K que torna a raíz :
E agora, vamos ber qual valor de faz com que a raíz seja :
Sendo assim, a faixa do ganho para o processo ser estável será:
Na maioria das vezes, vamos tentar evitar ganhos negativos, portanto:
Resposta
Exercício Resolvido #7
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 13.8
Dado , em que utilize o critério de Routh-Hurtwitz para determinar o número de polos de dentro, fora e sobre o círculo unitário. O sistema é estável?
Passo 1
Esse exercício jpa começa nos dando logo de cara a equação característica do sistema, que é:
É da equação característica que podemos tirar as informações sobre estabilidade do sistema. Só que a gente vai usar o método de Royht-Hurwitz para fazer isso, e esse método foi desenvolvido e funciona apenas no plano .
Então precisamos fazer uma adaptação, e para isso, usaremos a transformação bilinear. A transformação bilinear faz uma troca de variáveis, entre e conforme a expressão abaixo:
Vamos aplicar a transformação bilinear na nossa equação característica então:
Passo 2
Multiplicando toda a expressão por :
Expandindo os termos exponenciais:
Efetuando as multiplicações e juntando os termos iguais:
Passo 3
Agora que já temos a equação característica no plano , podemos aplicar o Critério de Routh.
O diagrama de Routh para essa equação será:

Caso você não se lembre como construir um diagrama de Routh seria legal dar uma revisada na aula de Critério de estabilidade de Routh-Hurwitz.
O critério diz que a cada mudança de sinal na primeira coluna, existe uma raíz instável. Como houve uma mudança de sinal na primeira coluna apenas da primeira para a segunda linha, existe uma raíz instável, isto é, uma raiz com parte real positiva no plano , ou uma raiz dentro do circulo unitário com centro na origem no plano .
Como não tivemos uma linha de zeros, é impossível que haja raízes sobre o eixo dos imaginários no plano ou sobre a linha do cícrculo unitário no plano . Portanto, as outras duas raízes se encontram no semiplano esquerdo ou dentro do círculo unitário no plano .
Portanto o sistema é instável.
Resposta
Sistema instável. Duas raízes dentro do círculo unitário com centro na origem e uma fora.
Exercício Resolvido #8
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 13.6
Dado , em que utilize o critério de Routh-Hurtwitz para determinar o número de polos de dentro, fora e sobre o círculo unitário. O sistema é estável?
Passo 1
Esse exercício jpa começa nos dando logo de cara a equação característica do sistema, que é:
É da equação característica que podemos tirar as informações sobre estabilidade do sistema. Só que a gente vai usar o método de Royht-Hurwitz para fazer isso, e esse método foi desenvolvido e funciona apenas no plano .
Então precisamos fazer uma adaptação, e para isso, usaremos a transformação bilinear. A transformação bilinear faz uma troca de variáveis, entre e conforme a expressão abaixo:
Vamos aplicar a transformação bilinear na nossa equação característica então:
Passo 2
Multiplicando toda a expressão por :
Expandindo os termos exponenciais:
Efetuando as multiplicações e juntando os termos iguais:
Passo 3
Agora que já temos a equação característica no plano , podemos aplicar o Critério de Routh.
O diagrama de Routh para essa equação será:

Caso você não se lembre como construir um diagrama de Routh seria legal dar uma revisada na aula de Critério de estabilidade de Routh-Hurwitz.
O critério diz que a cada mudança de sinal na primeira coluna, existe uma raíz instável. Como houve uma mudança de sinal na primeira coluna apenas da primeira para a segunda linha, existe uma raíz instável, isto é, uma raiz com parte real positiva no plano , ou uma raiz dentro do circulo unitário com centro na origem no plano .
Como não tivemos uma linha de zeros, é impossível que haja raízes sobre o eixo dos imaginários no plano ou sobre a linha do cícrculo unitário no plano . Portanto, as outras duas raízes se encontram no semiplano esquerdo ou dentro do círculo unitário no plano .
Portanto o sistema é instável.
Resposta
Sistema instável. Duas raízes dentro do círculo unitário com centro na origem e uma fora.