Projeto de controlador cascata
Teoria
Introdução
O controle cascata é aquela técnica de controle quase perfeita que corrige os distúrbios do sistema de forma rápida e eficiente.
Nele, temos uma variável primária e uma variável secundária que juntas promovem o controle da variável controlada de maneira extremamente eficiente.
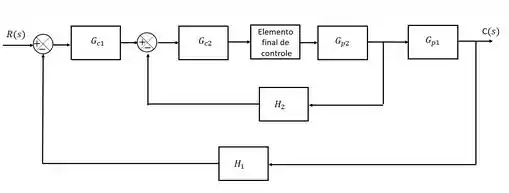
No controle cascata nós temos duas variáveis medidas, e consequentemente, temos também dois controladores. O controlador primário, também chamado de mestre, e o controlador secundário, também chamado de escravo. O controlador primário é quem define o setpoint do controlador secundário.
E se temos dois controladores, nós precisamos sintonizar esses dois controladores, isto é, acertar os valores de seus parâmetros (ganho, constante de tempo integral e constante de tempo derivativo) de modo que o funcionamento do sistema de controle seja o mais otimizado possível.
Entretanto, como a malha primária e a malha secundária estão intricadas uma na outra, a tarefa de sintonizar esses dois controladores não é muito simples.
A verdade é que não existe um método certo e eficaz de se sintonizar controladores em cascata. Hoje vamos ver um método que, apesar de limitado, é consideravelmente bom na sintonização desses controladores.
Método de Austin e Lopez
Este método, que foi proposto por Austin (1986) e posteriormente aprimorado por Lopez (2003), apresenta técnicas de sintonização tanto do controlador primário quanto do secundário.
O método consiste na introdução de um sinal de degrau no elemento final de controle e após isso gravar a resposta da variável primária e secundária.
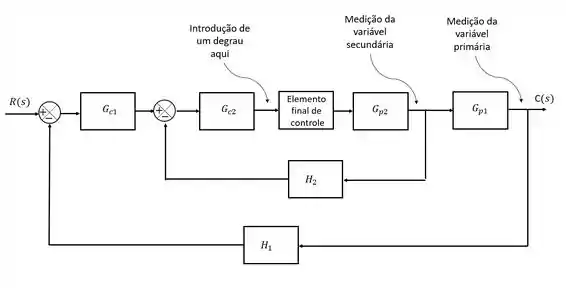
Dessa forma, aumenta-se em uma unidade o sinal para o elemento final de controle e observa-se a resposta tanto da variável secundária quanto da variável primária ao longo do tempo, gerando-se dois gráficos no final.
Os gráficos gerados, vão ser aqueles que a gente já conhece e que vamos aproximar para um modelo FOPDT (primeira ordem mais tempo morto). Se você não se lembra disso, é legal dar uma revisada na aula sobre métodos de Ziegler-Nichols.
O gráfico FOPDT é aquele assim:
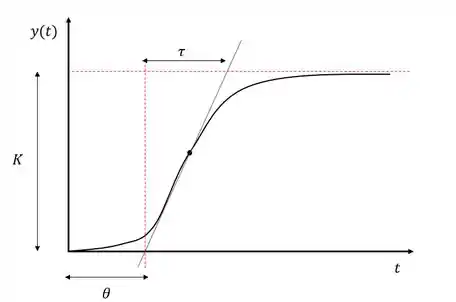
Dessa forma teremos duas funções FOPDT, uma para o processo primário e outra para o processo secundário:
E
Sintonia do controlador secundário
Sempre que formos sintonizar dois controladores em cascata, devemos sempre começar pelo controlador secundário. Sendo assim, a sintonização é feita sempre de dentro para fora.
No controle cascata, convencionalmente se usa controladores P ou PI como o secundário, e PI ou PID como o primário.
A sintonização do controlador secundário é feita pelos métodos que a gente já conhece (Ziegler-Nichols ou Cohen-Coon). A tabela de sintonização do controlador secundário usando Ziegler-Nichols será então:
Ou usando Cohen-Coon:
Com
Método de Austin e Lopez
Para o cálculo dos parâmetros do controlador primário, usaremos as correlações de Lopez e Austin. Usando os valores dos parâmetros das funções de transferência FOPDT obtidas.
Repare que existe uma correlação diferente para cada tipo de combinação entre o controlador secundário e o controlador primário.
Isso quer dizer, basicamente, que a correlação usada para fazer a sintonia do controlador primário depende do tipo de controlador secundário que está sendo usado.
Além disso, outro ponto crucial é que as correlações são limitadas por uma faixa de aplicação. Cada combinação tem sua própria faixa e a gente deve sempre checar se o nosso processo está dentro daquela faixa antes de usarmos a correlação que queremos.
Método de Austin e Lopez
Sintonia do controlador secundário
Método de Austin e Lopez
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um engenheiro de controle desejava implementar um sistema de controle cascata em um dos processos pelos quais era responsável visto os vários benefícios agregados pelo controle em cascata em comparação com o controle feedback simples.
Sendo assim, o engenheiro estudou o processo que desejava aplicar o controle em cascata e definiu a variável primária e secundária que seriam usadas.
O próximo passo seria sintonizar os dois controladores, para isso, ele introduziu um degrau unitário no elemento final de controle e registrou a resposta da variável primária e da variável secundária que ele havia escolhido. Com esse registro das respostas ao longo do tempo, ele conseguiu traçar o modelo FOPDT (primeira ordem mais tempo morto) das respostas:
Ao chegar nessa etapa ele notou que não seria possível implementar o controle cascata da forma que ele havia determinado. Explique o motivo e dê uma sugestão do que poderia ser feito.
Passo 1
Uma das exigências para se implementar o controle em cascata é que a variável secundária deve responder mais rapidamente à variações do que a variável primária.
Através dos modelos FOPDT mostrado acima, podemos ver que:
Como a constante de tempo do processo da variável secundária é maior do que da variável primária, isso indica que a variável secundária é mais lenta do que a primária, impossibilitando assim o uso do controle cascata com essas escolhas de variáveis.
Passo 2
De fato, se olharmos a tabela com as correlações de Austin e Lopez abaixo podemos ver que a razão deve ser sempre menor que 0,7, não importa qual combinação de controladores seja escolhida.
No exemplo dado temos:
O que está totalmente fora da faixa desejada.
Resposta
Sendo assim, o pobre engenheiro de controle deverá tentar identificar uma outra variável intermediária que responda mais rapidamente que a variável primária.
Caso não seja possível, ele ainda pode tentar identificar um distúrbio que possa ser medido para implementar um controle feedforward em paralelo com o feedback de forma a otimizar o controle.
Exercício Resolvido #2
Elaboração própria
Como queria implementar uma malha em cascata para controlar a temperatura de um reator, um engenheiro de controle precisava decidir qual variável intermediária seria mais adequada para usar como variável secudária na malha.
Para isso ele fez o teste de ralé (inserção de um degrau e monitoramento da resposta) na variável primária e nas duas variáveis candidadatas a se tornarem a variável secundária.
Para a variável primária, foi obtida seguinte curva de reação:
Para a a primeira variável intermediária testada, a curva de resposta é dada abaixo:
Já para a segunda opção de variável secunária, o gráfico da resposta de reação é dado abaixo:
Indique e justifique qual é a melhor opção de escolha para a variável secunária: a primeira ou a segunda opção?
Passo 1
Para a escolha da variável secundária de uma malha em cascata o critério predominante a ser levado em consideração é a velocidade de resposta a distúrbios.
A variável secundária deve responder mais rapidamente que a variável primária. Alguns autores dizem que o ideal é que a variável secundária seja três vezes mais rápido, entretanto, quando a variável secundária tem constante de tempo 70% menor que a primária o efeito na malha de controle já começa a aparecer.
Sendo assim, podemos vez que no enunciado temos o gráfico de resposta da variável primária que usaremos como referência para comparar com os outros dois gráficos dados.
Fazendo a análise visual dos gráficos, podemos ver que a resposta referente à primeira opção de variável secundária é levemente mais rápida que da variável primária, o que não é o ideal.
Já a segunda opção de variável secundária apresenta uma resposta consideravelmente mais rápida que a variável primária, e portanto, essa variável deverá ser escolhida para ser a variável secundária do projeto.
Resposta
Segunda opção.
Exercício Resolvido #3
Elaboração própria
Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e foi possível aproximar as funções de transferência da malha secundária e primária a um modelo FOPDT como mostrado abaixo:
Sintonize ambos os controladores do sistema em cascata utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária. Suponha um controlador P secundário e um PI primário
Passo 1
Quando sintonizamos uma malha em cascata, sempre sintonizamos os controladores de dentro primeiro, portanto vamos começar sintonizando o controlador secundário.
O enunciado já nos deu a função FOPDT da variável secundária e dela podemos extrair as constantes:
Caso você tenha alguma dúvida nesse passo, seria bacana dar uma olhada no material de Métodos de Ziegler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
O enunciado pediu que o controlador secundário fosse do tipo P, sendo assim:
Passo 2
Agora precisamos sintonizar o controlador primário. O enunciado também nos deu a função FOPDT da variável primária, e dela conseguimos extrair as seguintes constante:
Aí com esses valores a gente pega a tabela abixo para sintonizar o controlador primário:
Como o nosso controlador primário é PI e o secundário é P vamos usar as fórmulas do primeiro quadrante da tabela acima.
Mas antes de sair aplicando as correlações, precisamos conferir se estamos dentro da faixa adequada para usar o método:
Opa tudo certo, podemos seguir!
Passo 3
Finalmente podemos aplicar as correlações da tabela para encontrar os parâmetros do controlador primário:
O nosso PI primário ficará portanto
Resposta
Exercício Resolvido #4
Elaboração própria
Deseja-se sintonizar uma malha em cascata em dois níveis. Para obter os parâmetros de sintonização, introduziu-se um degrau unitário no elemento final de controle e registrou-se as resposta da variável secundária e primária. Após análise das curvas de reação, pode-se deduzir os seguinte modelos FOPDT (primeira ordem mais tempo morto) para as variáveis secundárias e primárias respectivamente:
Sintonize ambos os controladores do sistema em cascata utilizando as correlações de Cohen-Coon para a malha secundária e de Austin e Lopez para a malha primária. Suponha que ambos os controladores sejam do tipo PI.
Passo 1
O primeiro passo quando estamos sintonizando controladores em cascata é sempre começar de dentro para fora, portanto, devemos começar pelo controlador secundário. Para fazer a sintonização desse controlador vamos usar as correlações de Cohen-Coon e para isso precisamos dos parâmetros do modelo FOPDT para essa variável.
O enunciado já nos deu a função FOPDT da variável secundária e dela podemos extrair as constantes:
Antes de fazer a sintonização do controlador, vamos checar se os parâmetros estão na faixa permitida pelo método:
Como a faixa aceitável é está tudo certo e podemos prosseguir.
Vamos usar a tabela abaixo para fazer a sintonia do controlador:
Como queremos um controlador do tipo PI:
Portanto, o controlador secundário será:
Passo 2
Agora precisamos sintonizar o controlador primário. O enunciado também nos deu a função FOPDT da variável primária, e dela conseguimos extrair as seguintes constante:
Com isso, nós consultamos a tabela abaixo para saber qual correlação devemos usar
Como ambos os controladores são do tipo PI, vamos usar as correlações que estão no canto inferior esquerdo.
Mas antes de sair aplicando as correlações, precisamos conferir se estamos dentro da faixa adequada para usar o método:
Tudo dentro do intervalo que precisamos, podemos prosseguir!
Passo 3
Finalmente podemos aplicar as correlações da tabela para encontrar os parâmetros do controlador primário:
O nosso PI primário ficará portanto
Resposta
Exercício Resolvido #5
Elaboração própria
Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e foi possível aproximar as funções de transferência da malha secundária e primária a um modelo FOPDT como mostrado abaixo:
Sintonize ambos os controladores do sistema, sendo o secundário um controlador P e o primário um controlador PID, utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária.
Passo 1
O primeiro passo sempre será sintonizar o controlador secundário, pois a sintonização de uma malha cascata sempre é feita de dentro para fora.
Pelo enunciado, já podemos tirar os parâmetros do modelos FOPDT para a variável secundária:
Caso você tenha alguma dúvida nesse passo, seria bacana dar uma olhada no material de Métodos de Ziegler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como o controlador secundário é do tipo P, vamos usar as correlações da primeira linha
Passo 2
Para o controlador primário devemos usar as correlações de Austin e Lopez mostradas na tabela abaixo. Para isso usaremos os parâmetros FOPDT da malha primária que também foram dados no enunciado:
O controlador secundário que sintonizamos no passo anterior era do tipo P, e o primário que estamos sintonizando agora é do tipo PID, portanto, usamos as correlações do canto superior direito da tabela.
Mas antes de aplicar as correlações, vamos conferir se tudo está dentro das faixas necessárias:
Perfeito! Podemos prosseguir!
Passo 3
Vamos então aplicar as correlações do quadrante superior direito para sintonizar o controlador primário:
O nosso PI primário ficará portanto
Resposta
Exercício Resolvido #6
Elaboração própria
Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e estão mostrados abaixo respectivamente.
Sintonize ambos os controladores da malha cascata utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária. Suponha um controlador PI secundário e um PID primário
Passo 1
A sintonia do controle em cascata sempre é feita de dentro para fora, sendo assim, o primerio passo sempre será controlar o controlador mais interno, ou seja, o controlador secundário. Sendo assim, vamos definir a função FOPDT para a malha interna:
Dessa forma, podemos estimar nossas constantes como:
Se você não lembra como estimar uma função FOPDT seria legal dar uma revisada na aula de Zigler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como queremos um controlador PI:
Sendo assim, o controlador interno (secundário) terá função de transferência:
Passo 2
Para sintonizar o segundo controlador, precisamos determinar a função FOPDT para a variável primária:
Com esse esboço, podemos estimar nossas constantes como:
Com esses valores, conseguimos sintonizar o PID usando a tabela abaixo:
Como o controlador secundário foi um PI e o primário será um PID, as correlações que usaremos serão as do último quadrante da tabela acima.
Entretanto, antes de sintonizar, precisamos conferir se os parâmetros que encontramos estão na faixa adequada:
Sendo assim, estamos dentro das especificações.
Passo 3
Vamos aplicar as correlações da tabela para finalmente conseguir sintonizar o controlador:
Portanto, teremos o seguinte controlador PID primário:
Resposta
Exercício Resolvido #7
Elaboração própria
Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os gráficos de curva de reação para a variável primária e secundária foram registrados e estão mostrados abaixo, respectivamente:
Faça a sintonização dos controladores em casacada. Utilize as correlações de Ziegler-Nichols para o controlador secundário e de Austin e Lopez para o controlador primário. Suponha que o controlador secundário seja do tipo P e o primário é do tipo PI.
Passo 1
Como a sintonia em cascata sempre é feita de dentro para fora, primeiro devemos sintonizar a malha secundária. Para isso, vamos tentar descobri os parâmetros FOPDT a partir do gráfico dado:
Dessa forma, podemos estimar nossas constantes como:
Se você não lembra como estimar uma função FOPDT seria legal dar uma revisada na aula de Zigler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como queremos um controlador P:
Sendo assim, o controlador interno (secundário) terá função de transferência:
Passo 2
Agora que já sintonizamos o controlador secundário, podemos partir para o primário. Sendo assim, vamos fazer o mesmo que fizemos anteriormente para a variável primária:
Com esse esboço, podemos estimar nossas constantes como:
Agora, vamos consultar a tabela com as correlações de Austin e Loez para saber quais correlações deverão ser usadas.
O nosso controlador secundário era do tipo P, e o primário será do tipo PI, logo, devemos usar as correlações que estão no canto superior esquerdo da tabela.
Porém, antes de sintonizar, precisamos conferir se os parâmetros que encontramos estão na faixa adequada:
Maravilha! Tudo certo.
Passo 3
Vamos aplicar as correlações da tabela para finalmente conseguir sintonizar o controlador:
O nosso PI primário ficará portanto
Resposta
Exercício Resolvido #8
Elaboração própria
Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os gráficos de curva de reação para a variável primária e secundária foram registrados e estão mostrados abaixo, respectivamente:
Faça a sintonização dos controladores em casacada. Utilize as correlações de Ziegler-Nichols para o controlador secundário e de Austin e Lopez para o controlador primário. Suponha que o controlador secundário seja do tipo PI e o primário é do tipo PID.
Passo 1
Devemos sempre começar pelo controlador mais a dentro na malha, nesse caso, o controlador secundário. Vamos primeiro estimar os parâmetros da FOPDT dessa malha usando o esboço abaixo:
Com esse esboço, podemos estimar nossas constantes como:
Se você não lembra como estimar uma função FOPDT seria legal dar uma revisada na aula de Zigler-Nichols.
Com esse valores, podemos sintonizar o controlador secundário usando a tabela de Ziegler-Nichols:
Como queremos um controlador PI:
Sendo assim, o controlador interno (secundário) terá função de transferência:
Passo 2
Vamos aplicar o mesmo procedimento agora para estimar a função FOPDT para a malha primária:
Com esse esboço, podemos estimar nossas constantes como:
Agora, podemos sintonizar o controlador primário consultando a tabela abaixo:
Nesse exercício o controlador secundário é PI e o primário é PID, então usamos as correlaçãoes que estão no canto inferior direito da tabela.
Porém, antes de sintonizar, precisamos conferir se os parâmetros que encontramos estão na faixa adequada:
Maravilha! Tudo certo.
Passo 3
Vamos aplicar as correlações da tabela para finalmente conseguir sintonizar o controlador:
O nosso PI primário ficará portanto