Sistemas multivariável
Produzido por Alexandre NunesTeoria
Introdução
Tudo o que a gente estudou em controle de processos até aqui a gente tinha um objetivo bem simples: controlar uma variável do nosso processo manipulando uma outra variável do processo.
Esse tipo de controle é chamado de controle SISO, que quer dizer single input, single output, ou em bom português, “entrada única e saída única”.
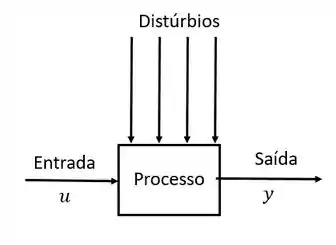
Mas não existe apenas o controle SISO. Vamos pensar num exemplo.
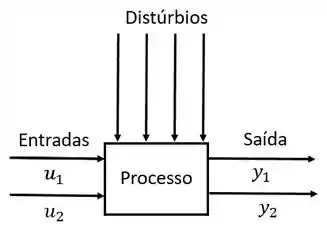
Imagina que você está controlando o produto de um reator, e você precisa garantir a quantidade e a qualidade da sua produção, ou seja, você precisa controlar a vazão do produto e também a composição do produto. Imagina também que esse reator possui duas correntes de entrada que podem ser controladas.
Esse é um exemplo clássico de um controle MIMO (tutupom?) que significa multiple input, multipli output, que na língua tupiniquim significa “várias entradas, várias saídas”
Um tanque de mistura
Imagine que a gente tenha um tanque de mistura com duas correntes de entrada, e assim como no exemplo que eu dei acima, a gente precisa controlar a vazão e a concentração da corrente de saída.
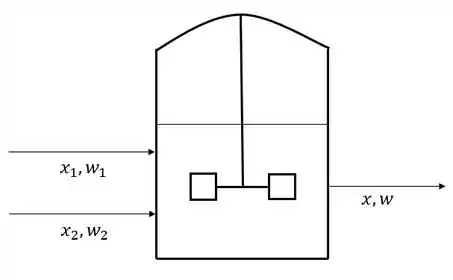
Nesse exemplo, teremos duas variáveis de saída (respostas do processo) que são e . Como entrada do processo teremos as duas vazões de entrada que são as variáveis de entrada que podemos controlar com uma válvula por exemplo. e vamos considerar como distúrbios.
Antes de analisar esse processo multivariável, vamos entender um pouco melhor a sua dinâmica.
Esse tanque foi projetado para trabalhar com os seguintes valores em estado estacionário:
O balanço de massa global do processo nos permite encontrar :
Já o balanço por componente nos permite encontrar a concentração da saída:
Ganho em malha aberta e em malha fechada
Quando a gente estava trabalhando com controle SISO, a forma de se calcular o ganho era bem direta. Pela definição, ganho é a razão entre a variação da saída, dada uma certa variação da entrada.
Quando estivermos trabalhando com controle MIMO, será muito importante saber como cada saída vai reagir dependendo da variação de cada resposta, ou seja, precisamos saber determinar o ganho de cada saída com relação a cada entrada.
Num processo como o do nosso exemplo, com duas entradas e duas saídas, teremos quatro possíveis combinações de entradas com saída.
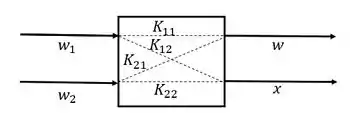
O ganho , por exemplo, seria o ganho referente à saída composição do produto, com a entrada vazão da corrente 2.
Uma forma de calcular o ganho , é aplicar uma variação em e observar como a composição do produto varia, mantendo-se a outra entrada ( ) constante:
Vamos imaginar, se a vazão da corrente aumentar para (um aumento de em relação ao estado estacionário), aplicando as equações do balanço obteremos uma nova composição de saída:
Logo, o ganho será:
Esse ganho, que é calculado mantendo-se as outras entradas constantes é chamado de ganho de malha aberta.
Entretanto, também podemos calcular o ganho mantendo-se a outra saída constante, ao invés da entrada.
Vamos voltar ao exemplo anterior, nós aumentamos a de para , e isso causou uma variação na composição de para .
Agora nós queremos encontrar a variação de quando permanece constante, então se foi aumentada em , para compensar isso, devemos diminuir de para , de forma que a vazão de saída, , permaneça em .
Quando é e é , a composição da saída, , passa a ser .
Sendo assim, o nosso ganho quando mantemos a vazão de saída constante passa a ser:
O ganho calculado mantendo-se as outras saídas constantes é chamado de ganho de malha fechada.
Perceba que para um simples processo com duas entradas e duas saídas, nós temos oito ganhos diferentes: quatro ganhos de malha aberta e quatro ganhos de malha fechada.
Ganhos relativos
Por fim, para que fique mais fácil de visualizar como as saídas interagem com as entradas, é definido também uma medida de ganho relativo.
O ganho relativo é a razão entre o ganho em malha aberta e o ganho em malha fechada:
Com essa medida que acopla os dois tipos de ganho em um só, fica mais fácil de analisar a interação entre as saídas e as entradas.
Os ganhos relativos podem ser escritos em uma matriz chamada de RGA (Matriz de Ganhos Relativos). Para o nosso exemplo com duas entradas e duas saídas:
Tipos de interação
Por fim, um último conceito importante sobre sistemas MIMO é o tipo de interação entra as variáveis.
No exemplo anterior, nós encontramos um ganho em malha aberta igual a . Quando nós fechamos a malha e calculamos novamente o ganho, encontramos , ou seja, houve um aumento. Isto ocorre porque as malhas não “lutam” uma com outra, pelo contrário, o fechamento de uma malha é positivo para a outra. Portanto dizemos que ocorre uma interação positiva. Quando o fechamento da malha faz com que a variável diminua, significa que as duas malhas estão em conflito, e teremos, portanto, uma interação negativa.
Podemos ver o tipo de interação pelo ganho relativo. Malhas com interação positiva terão ganho relativo positivo e menor que 1. Malhas com interação negativa terão ganho relativo negativo ou maior que 1.
Ganho em malha aberta e em malha fechada
Ganhos relativos
Tipos de interação
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Dadas as duas matrizes de ganho relativo para dois diferentes sistemas mostradas abaixo. Classifique a inteação entre os sistemas como sendo positiva ou negativa.
Passo 1
Para classificar o sistemas como de interação positiva ou de interação negativa precisamos apenas avaliar s ganhos relativos. Se os valores de ganho relativo foram entre e a interação entre as malhas é dita positiva. Se os ganhos relativos forem maior que ou negativos a interação é negativa.
Sendo assim, a representa a matriz de ganhos relativos de um sistema mutivariável de interação negativa enquanto a representa uma matriz para um sistema com interação positiva.
Resposta
Interação negativa
Interação positiva
Exercício Resolvido #2
Elaboração própria
Sabendo-se que o ganho relativo de uma variável em relação a uma variável é e que o ganho em malha aberta é , determine o valor de saída da variável quando a variável sofre uma perturbação degrau de ordem e todas as outras saídas são mantidas constantes. Considere que o valor de inicialmente era .
Passo 1
Para saber o valor final da variável quando sofre uma perturbação e as outras saídas se mantêm constantes, precisamos determinar o ganho em malha fechada desse par entrada/saída.
Como o enunciado forneceu o ganho em malha aberta e o ganho relativo, podemos calcular o ganho em malha fechada pela fórmula abaixo:
Como:
Teremos:
Passo 2
O ganho em malha fechada, pode ser definido como a variação da variável de saída pela variação da variável de entrada quando as outras saídas são constantes. Ou seja:
Pelo enunciado temos que:
Portanto:
Resposta
Exercício Resolvido #3
Elaboração própria
Sabe-se que o ganho relativo de uma variável em relação a uma variável é e que o ganho em malha fechada é . Uma perturbação é feita na variável fazendo com que ela passe de para , e todas as outras entradas são mantidas constantes. Qual será a variação sentida na variável ?
Passo 1
Para determinar a variação sofrida pela variável quando sofre uma perturbação e as outras entradas se mantêm constantes, precisamos determinar o ganho em malha aberta desse par entrada/saída.
Já temos o ganho relativo, e o ganho em malha fechada, o que possibilita o cálculo do ganho em malha aberta
Como:
Teremos:
Passo 2
O ganho em malha aberta, pode ser definido como a variação da variável de saída pela variação da variável de entrada quando as outras entradas são constantes. Ou seja:
Pelo enunciado temos que:
Portanto:
Resposta
Exercício Resolvido #4
Elaboração própria
Para que um trocador de não saia das especificações é necessária que tanto a temperatura de saída do fluito frio, , quanto a temperatura de saída do fluido quente, sejam controladas por um sistema de controle multivariável. Para que isso aconteça, as variáveis de entrada manipulada serão a vazão de entrada do fluido frio, , e a vazão de entrada do fluido quente, .
Sabe-se que quando a vazão de entrada do fluido quente varia de para a temperatura do fluido frio varia de para se permanecer constante e varia de para se se mantiver constante.
Calcule o ganho relativo entre a temperatura de saída do fluido frio e a vazão de entrada do fluido quente e diga se as malhas do sistema têm interação positiva ou negativa.
Passo 1
O ganho relativo é calculado como a razão entre o ganho de malha aberta e o ganho de malha fechada:
Vamos começar calculando o ganho em malha aberta, . O ganho em malha aberta é definido como a razão entra a variação da saída e a variação da entrada quando as outrs entradas permanecem iguais. Para o nosso exemplo:
Ou seja, quando é constante, teremos as seguintes variações:
Passo 2
Vamos calcular agora o ganho da temperatura em relação à vazão em malha fechada, ou seja, com constante.
Em malha fechada, para a mesma variação na vazão do fluido quente, a temperatura de saída do fluido frio varia de para , portanto:
Passo 3
O ganho relativo será portanto:
Sendo assim, dizemos que a interação entre as malhas é positiva uma vez que o ganho relativo está entre e .
Resposta
Interação positiva
Exercício Resolvido #5
Elaboração própria
Considere um reator com reação exotérmica do tipo:
Nesse reator, é desejado que tanto a temperatura da corrente de saída, , quanto a concentração do produto nessa corrente, , se mantenham num valor pré-definido. Para que esses requisitos sejam atendidos pode se manipular aa corrente de entrada do reagente no reator, , ou a vazão de fluido refrigerante na camisa que é usada para resfriar o tanque, .
Sabe-se que quando a vazão de fluido refrigerante na camisa passa de para mantendo-se a vazão constante, a temperatura da corrente de produto passa de para .
Se a mesma perturbação for feita na vazão de fluido refrigenrante, mas dessa vez mantendo-se a concentração do produto constante, a temperatura da corrente de saída passa de para
Calcule o ganho relativo entre a temperatura do produto do reator e a vazão de fluido regrigerante na camisa do reator. Aproveite e diga se as malhas têm interação positiva ou negativa.
Passo 1
O ganho relativo é calculado como a razão entre o ganho de malha aberta e o ganho de malha fechada:
Vamos começar calculando o ganho em malha aberta, . O ganho em malha aberta �� definido como a razão entra a variação da saída e a variação da entrada quando as outrs entradas permanecem iguais. Para o ganho da temperatura em relação à vazão do fluido refrigerante teremos:
Ou seja, quando é constante, teremos as seguintes variações:
Passo 2
Vamos calcular agora o ganho da temperatura da corrente de produto em relação à vazão de fluido refrigerante em malha fechada, ou seja, com constante.
Em malha fechada, para a mesma variação na vazão do fluido regrigerante, a teremos uma variação de na corrente de saída:
Passo 3
O ganho relativo será portanto:
Como o ganho relativo foi maior que a unidade, dizemos que a interação entre as malhas é negativa.
Isso acontece porque quando a malha é fechada, a variação da temperatura de saíde é de menor intensidade, o que indica que as malhas estão competindo entre si. Se a temperatura tivesse caída mais com o fechamento da malha, a interação seria positiva.
Resposta
Interação negativa.
Exercício Resolvido #6
Elaboração própria
Dado o sistema multivariável mostrado abaixo, onde e são as respostas e e são as entradas. Calcule
Sabe-se que os valores no estado estacionário são:
Passo 1
Primeiramente vamos calcular o valor das respostas em estado estacionário. Substituindo e teremos:
Passo 2
Como:
Precisamos calcular os dois ganhos, o de malha aberta e o de malha fechada.
O ganho é a relação entre a variação da saída com a entrada quando é constante.
Ou seja:
Vamos considerar uma variação unitária para e manteremos constante. Portanto:
Assim teremos:
Portanto o ganho será:
Passo 3
Agora vamos calcular o ganha em malha fechada que é a relação entre a variação de e quando é constante.
Vamos novamente fazer uma variação unitária em , mas temos que ver qual será a variação sofrida por para que fique constante:
Com:
Teremos :
Jogando na expressão para teremos:
Calculando :
Passo 4
Por fim, vamos calcular o ganho relativo:
Resposta
Exercício Resolvido #7
Elaboração própria
Dado o sistema multivariável mostrado abaixo, onde e são as respostas e e são as entradas.
Sabe-se que os valores no estado estacionário são:
As malhas tem interação positiva ou negativa?
Passo 1
Para calcular se a interalção entre as malhas é positiva ou negativa, devemos calcular qualquer um dos ganhos relativos. Se o ganho relativo estiver entre e a interação será positiva, entretanto, se for maior que ou negativo, a interação será negativa. Sendo assim, vamos calcular o ganho relativo e ver o que ele nos diz sobre a interação das malhar
Primeiramente vamos calcular o valor das respostas em estado estacionário. Substituindo e teremos:
Passo 2
Como:
Precisamos calcular os dois ganhos, o de malha aberta e o de malha fechada.
O ganho é a relação entre a variação da saída com a entrada quando é constante.
Ou seja:
Vamos considerar uma variação unitária para e manteremos constante. Portanto:
Calculando o novo :
Portanto o ganho será:
Passo 3
Agora vamos calcular o ganha em malha fechada que é a relação entre a variação de e quando é constante.
Vamos novamente fazer uma variação unitária em , mas temos que ver qual será a variação sofrida por para que fique constante:
Com:
Teremos :
Jogando na expressão para teremos:
Calculando :
Passo 4
Por fim, vamos calcular o ganho relativo:
Como o ganho relativo está entre e , a interação entre as malhas acontece de forma positiva.
Resposta
Interação positiva
Exercício Resolvido #8
Elaboração própria
Dado o sistema multivariável mostrado abaixo, onde e são as respostas e e são as entradas. Calcule
Sabe-se que os valores no estado estacionário são:
Passo 1
Primeiramente vamos calcular o valor das respostas em estado estacionário. Substituindo e teremos:
Passo 2
Como:
Precisamos calcular os dois ganhos, o de malha aberta e o de malha fechada.
O ganho é a relação entre a variação da saída com a entrada quando é constante.
Ou seja:
Vamos considerar uma variação unitária para e manteremos constante. Portanto:
Assim teremos:
Portanto o ganho será:
Passo 3
Agora vamos calcular o ganha em malha fechada que é a relação entre a variação de e quando é constante.
Vamos novamente fazer uma variação unitária em , mas temos que ver qual será a variação sofrida por para que fique constante:
Com:
Teremos :
Jogando na expressão para teremos:
Calculando :
Passo 4
Por fim, vamos calcular o ganho relativo: