Regras de emparelhamento e desacoplamento
Produzido por Alexandre NunesTeoria
Emparelhamento
No último tópico nós vimos a diferença entre ganho de malha aberta e de malha fechada, e também definimos ganho relativo que é a razão entra esses dois tipos de ganho.
O ganho relativo é importante porque através dele conseguimos definir como vamos emparelhar nosso sistema MIMO.
“Mas como assim emparelhar?”

Emparelhamento é como a gente vai combinar as entradas e saídas de forma que uma variável de entrada controle uma variável de saída sem que haja muita interferência das outras entradas.
Bugou? Calma, vou explicar melhor.
Imagina que você tenha duas saídas e duas entradas, e você precisa definir uma variável de entrada para ser manipulada caso a variável de saída saia do seu setpoint. Sendo assim, você precisa escolher a entrada ou a para controlar a saída . É importante que você escolha o par que tenha o máximo de interação possível.
Para saber qual par entrada-saída tem o maior grau de interação, é preciso analisar a matriz de ganho relativos do sistema. Por isso que a definição desse novo parâmetro é tão importante quando estamos trabalhando com sistemas multivariáveis.
Vamos entender as regras de emparelhamento fazendo um exemplo para um sistema 2x2.
Matriz de ganho relativo para sistema 2x2
Imagina que temos um sistema MIMO 2x2 da seguinte forma:
Nesse sistema, temos duas entradas, e , e duas saídas, e .
Vamos tentar calcular o ganho relativo da saída com relação a entrada . Ganho relativo é a razão entra o ganho em malha fechada e o ganho em malha aberta.
O ganho em malha aberta é a variação da saída, , dada uma certa variação na entrada, , quando as outras entradas estão constantes. Ele já vem na função de transferência do sistema e é o .
O ganho em malha fechada, já é um pouco mais difícil de encontrar. Ele é calculado como a variação da saída, , dada uma certa variação na entrada, , quando as outras saídas estão constantes.
Vamos tentar ver isso numericamente. Se as outras saídas estão constantes, então . Da equação teremos:
Substituindo em :
Sendo assim, o ganho em malha fechada será:
E o ganho relativo:
Olha que legal, dá para calcular o ganho relativo usando apenas os ganhos em malha aberta.
Ufa, calculamos então o ganho relativo para um dos quatro possíveis pares.
Nesse momento você já deve estar se desesperando e pensando que vai ter que fazer o mesmo processo quatro vezes né? Nada disso, trago boas notícias.
Se você fizer o mesmo processo para calcular o ganho relativo (se você quiser, pode fazer como exercício), verá que:
E os ganhos relativos e serão:
Sendo assim, se a gente chamar nosso ganho de . A matriz de ganhos relativos será sempre:
Regras de emparelhamento
Ok, encontramos uma forma de calcular nossa matriz de ganhos relativos, agora como fazemos para decidir como emparelhar nosso sistema?
Para isso, precisamos seguir a seguinte regra:
Para que o efeito da interação entre as malhas seja o menor possível, é preciso emparelhar as variáveis manipulada e controlada de forma que o ganho relativo esteja o mais próximo de possível.
Isso quer dizer que dada uma matriz de ganho relativos do tipo:
Se o valor de for próximo de , a maior interação acontecerá entre a saída e a entrada . Chamamos esse emparelhamento de 1-1/2-2.
Se o valor de for próximo de , a maior interação acontecerá entre a saída e a entrada . Chamamos esse emparelhamento de 1-2/2-1.
Quando é muito próximo de , a interação de cada saída com cada entrada é muito parecida e não é possível determinar qual par tem maior interação.
Devemos evitar um ganho relativo negativo o máximo possível. Sendo assim, para o melhor emparelhamento será o 1-2/2-1. E para será o 1-1/2-2.
Para sistemas de ordem superior a 2, como 3x3, 4x4 etc. O cálculo da matriz de ganhos relativos se torna muito complexo e a determinação do melhor acoplamento não é de tão fácil visualização. Para nós na graduação, , saber lidar com sistemas 2x2 já é bastante suficiente.
Desacoplamento de malhas
Show de bola! Vamos imaginar que você é o brabo do controle multivariável e já conseguiu montar sua matriz de ganho relativo e determinar o melhor emparelhamento possível.
Vamos supor que você encontrou esses valores aqui:
Sendo assim, seguindo as regras que a gente viu ali em cima, o melhor emparelhamento seria 1-1/2-2, uma vez que e está mais próximo de do que de .
Isso significa que você iria usar a variável de entrada para controlar a saída e a variável de entrada para controlar a saída . Entretanto, ainda existe uma certa interação cruzada, ou seja, a variável de entrada ainda influencia na saída e a entrada influencia na saída
Para fazer com que uma saída fique independente da entrada a qual ela não está emparelhada, faremos uso de uma ferramenta chamada de desacoplador.
Os desacopladores serão instrumentos que terão uma certa função de transferência projetada especificamente para impedir a influência cruzada entre as entradas e saídas que não estão emparelhadas.
Vamos imaginar um sistema 2x2 da seguinte forma:
Nesse exemplo, e são as respostas, e as entradas e , , e as funções de transferência para cada processo. O emparelhamento utilizado é o 1-1/2-2.
Sendo assim, precisamos que uma variação em não altere , e uma variação em não altere .
Fazendo igaul a :
Essa função de transferência que multiplica a entrada é o nosso desacoplador:
O subscrito é 12 porque esse é o desacoplador que mantêm a saída 1 constante para qualquer variação na entrada .
Para calcular o desacoplador devemos fazer o mesmo para a saída :
Logo:
Um detalhe é que se o emparelhamento entre as malhas for do tipo 1-2/2-1 os desacopladores têm fórmula um pouco diferente:
Só mais uma observação: os desacopladores precisam ser fisicamente realizáveis, ou seja, o grau do polinômio do numerador não pode ser maior que o grau do polinômio do denominador, além disso, O tempo morto da função de transferência do denominador, se existir, precisa ser maior que o tempo morto da função de transferência do denominador, se existir.
Regras de emparelhamento
Desacoplamento de malhas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Dado o sistema abaixo, calcule a RGA do sistema.
Passo 1
A RGA é a matriz dos ganhos relativos. Para calculá-la poderíamos calular os ganhos em malha aberta, depois os ganhos em malha fechada e dividir um pelo outro conforme a fórmula abaixo:
Entretnato, existe uma maneira mais fácil de fazer isso, que é apenas usando os ganhos em malha aberta.
Os ganhos em malha aberta são as constantes que multiplicam as entradas. Dessa forma,o ganho em malha aberta que relaciona a saída com a entrada é .
Vamos então escrever os quatro ganhos em malha aberta em forma de matrix:
Passo 2
Com os quatro ganhos em malha aberta, nós podemos calcular o ganho relativo conforme a fórmula abaixo:
Substituindo os valores a matriz de ganhos em laha aberta teremos:
Passo 3
Por ser um sistema 2x2, com o primeiro ganho relativo nós conseguimos determinar todos os outros da seguinte maneira:
Sendo que .
Portanto, a nossa matriz RGA será:
Resposta
Exercício Resolvido #2
Elaboração própria
Dada a matriz de ganhos em malha aberta determine o melhor emparelhamento entre as malhas.
Passo 1
Bom, o enunciado nos deu os ganho em malha aberta. A boa notícia é que com os ganho em malha aberta nós conseguimos encontrar a matriz de ganhos relativos, RGA, e com a RGA nós conseguimos definir o melhor emparelhamento.
Para isso, podemos começar calculando o ganho relativo conforme a fórmula abaixo:
Substituindo os valores dados no enunciado teremos:
Passo 2
Para calcular a RGA, podemos usar o modelo abaixo:
Sendo:
Portanto:
Passo 3
Agora para definir qual melhor interação devemos seguir duas regras:
- A melhor interação é aquela que tem ganho relativo mais próximo de .
- Evitar ao máximo relacionar variáveis com ganho relativo negativo.
Sendo assm, as duas regras mostram que a melhor interação é 1-2/2-1.
Isso porque o ganho relativo referente a saída 1 com a entrada 1 apresenta valor que é negativo e mais longe de 1 do que o ganho relativo referente a saída 1 com a entrada 2.
Resposta
Emparelhamento 1-2/2-1
Exercício Resolvido #3
Professora Ninoska Bojorge – Lista 5, 2015.1, UFF, Questão 4.a
Avaliar a RGA, e sugerir um esquema de emparelhamento para o seguinte processo:

Passo 1
Neste exercício precisamos determinar a matriz de ganho relativo para o processo e depois dizer qual será a melhor forma de emparelhar as saídas e entradas.
Nesse exercício foi dado uma matriz com as funções de transferências que relacionam as saídas com as entradas, e dessas funções nós conseguimos extrais o ganho em malha aberta.
O ganho em malha aberta é a constante que multiplica a função de transferência, sendo assim podemos gerar uma matriz apenas com os ganhos em malha aberta do processo:
Passo 2
Com todos os ganhos em malha aberta é possível calcular o ganho relativo, através da fórmula abaixo:
Substituindo os calores da matriz de ganho em malha aberta, teremos:
A RGA pode ser calculada então da seguinte forma:
Sendo:
Portanto:
Passo 3
Agora devemos definir qual melhor interação. Para isso devemos seguir duas regras:
- A melhor interação é aquela que tem ganho relativo mais próximo de .
- Evitar ao máximo relacionar variáveis com ganho relativo negativo.
Sendo assm, as duas regras mostram que a melhor interação é 1-1/2-2.
Isso porque o ganho relativo referente a saída 1 com a entrada 1 apresenta valor que é mais próximo de do que o ganho relativo referente à saída 1 com a entrada 2 que é .
Além disso, o emparelhamento 1-2/2-1 relaciona variáveis com ganhos relativos negativos, o que não é desejado
Resposta
Emparelhamento 1-1/2-2
Exercício Resolvido #4
Professora Ninoska Bojorge – Lista 5, 2015.1, UFF, Questão 4.b
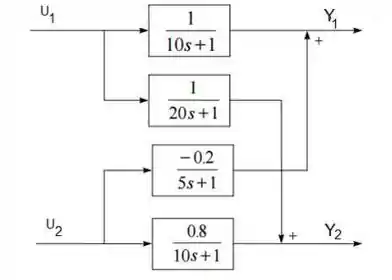
Avaliar a RGA, e sugerir um esquema de emparelhamento para o seguinte processo:
Passo 1
Precisamos calcular a RGA e dizer o melhor emparelhamento para esse conjunto de saídas e entradas. Entretanto, nesse exercício o que foi dado foi como as saídas se relacionam com as entradas sob a forma de diagrama de blocos.
Sendo assim, podemos inferir desse diagrama de blocos que a função de transferência que relaciona a saída com a entrada é:
Da mesma forma a a função de transferência que relaciona a saída com a entrada é:
E analogamente teremos:
Com as funções em malha aberta definidas, é possível determinar a matriz de ganhos em malha aberta.
O ganho em malha aberta é a constante que multiplica a função de transferência, sendo assim podemos gerar uma matriz apenas com os ganhos em malha aberta do processo:
Passo 2
Com todos os ganhos em malha aberta é possível calcular o ganho relativo, através da fórmula abaixo:
Substituindo os calores da matriz de ganho em malha aberta, teremos:
A RGA pode ser calculada então da seguinte forma:
Sendo:
Portanto:
Passo 3
Agora devemos definir qual melhor interação. Para isso devemos seguir duas regras:
- A melhor interação é aquela que tem ganho relativo mais próximo de .
- Evitar ao máximo relacionar variáveis com ganho relativo negativo.
Nesse caso não temos ganho relativo negativo, o qur já facilita o nosso lado. Temos que ver então qual par vai ter ganho relativo mais próximo de .
Sendo assim, o emparelhamento perfeito vai ser entre o 1-1/2-2 uma vez que o ganho relativo para esse emparelhamento será que é mais próximo de do que .
Ou seja, vamos emparelhar a saída com e a saída com .
Resposta
Emparelhamento 1-1/2-2
Exercício Resolvido #5
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 406, Problema 12-6.
Um exemplo de malhas de controle altamente interativas é o controle de composição do topo e da base em uma coluna de destilação. Dois testes foram efetuados em uma simulação de uma coluna de butano-pentano: um foi a variação no fluxo de vapor mantendo o fluxo de refluxo constante, o outro foi uma variação no fluxo de refluxo mantendo o fluxo de vapor constante. A tabela a seguir resume os fluxos e as composições para cada um dos testes, após o estado estacionário ser estabelecido.

As variáveis controladas são a percentagem de butano na base e nos produtos destilados, e as variáveis manipuladas são os pontos fixos de fluxo de vapor e de fluxo de refluxo. Calcule os ganhos da malha aberta em estado estacionário e os ganhos relativos para os dois emparelhamentos possíveis. A interação é positiva ou negativa? Qual variável deve ser manipulada para controlar a composição do destilado para que a interação entre as duas malhas seja minimizada? Qual é o ganho de estado estacionário para a malha de composição do destilado quando a malha de composição da base está fechada?
Passo 1
Esse exercício pede um monte de coisa da gente, então vamos com bastante calma.
Ele coloca para gente um problema onde temos duas variáveis que desejamos controlar que são as percentagens de butano tanto na base quanto no destilado. Essas variáveis poderão ser controladas através de duas variáveis de entrada, que são o fluxo de vapor no refervedor e o fluxo de refluxo, ou simplesmente, taxa de refluxo.
Para começar simplificando o problema, vamos chamar as saídas de e e as entradas de e . Então teremos a nova tabela abaixo:

Passo 2
Para encontrar tudo que o exercício pede, foram feitos testes. Nesses testes primeiramente foi implementada uma variação em uma entrada, e manteve-se a outra constante. Depois foi feito o mesmo com a entrada que ficou constante no primeiro teste.
Sendo assim, podemos calcular os ganhos em malha aberta dessas malhas. O ganho em malha aberta é referente à variação da saída mediante uma variação em uma entrada quando as outras entradas estão constantes.
Podemos escrever isso matematicamente assim:
Sendo assim, o ganho , que reaciona com , poderá ser encontrado usando o teste 1, porque nesse teste, se manteve constante. Portanto:
Da mesma forma o ganho será:
Os ganhos e podem ser encontrados usando o teste 2 uma vez que eles são os ganhos das saídas e com relação à entrada , portanto, é necessário que esteja mantido constante.
Podemos organizar esses ganhos em uma matriz de ganhos em malha aberta:
Passo 3
Já calculamos a primeira coisa que foi pedida que foram os ganhos em malha aberta. Agora podemos usar esses ganhos para calcular os ganhos relativos para esse sistema. Como se trata de um sistema podemos usar a fórmula abaixo para calcular o ganho :
Sunstituindo os valores encontrados anteriormente, teremos:
A matriz de ganhos relativos, também conhecida como RGA, poderá ser definida completamente conforme abaixo:
Sendo .
Portanto:
Passo 4
Com os ganhos relativos calculados, podemos classificar as malhas como tendo interação positiva ou negativa. Como os ganhos relativos são ou maiores que ou negativos, as malhas são classificadas como tendo interação negativa.
Além disso, podemos definir o melhor emparelhamento. Para isso devemos escolher o par que apresenta o ganho relativo mais próximo de e que não seja negativo. Neste caso o melhor emparelhamento será o 1-1/2-2. Ou seja: emparelhar a percentagem de butano na base com o fluxo de vapor e a percentagem de butano no destilado com o fluxo do refluxo.
Passo 5
Por fim, precisamos calcular o ganho em malha fechada do percentual de butano no destilado com relação a sua entrada, que como vimos é o fluxo de refluxo, . Como já temos o ganho em malha aberta e o ganho relativo, podemos usar a fórmula abaixo para fazer o cálculo:
Resposta
Interação negativa.
Emparelhamento 1-1/2-2
Exercício Resolvido #6
Elaboração própria
Dada a matriz de funções de transferência abaixa, determine o melhor emparelhamento entre as malhas e projete os desacopladores adequados.
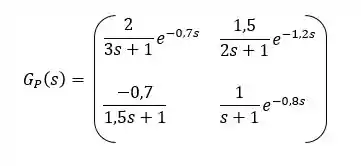
Passo 1
Para determinar o melhor emparelhamento nós precisamos primeiro determinar a matriz de ganhos relativos RGA.
Para determinar essa matriz, usaremos os ganhos em malha aberta que podem ser encontrados nas funções de transferência dadas no enunciado.
Os ganhos em malha aberta são as constantes que multiplicam as funções de transferência, sendo assim, a gente consegue montar nossa matriz de ganhos em malha aberta:
Passo 2
Com a matriz de ganhos em malha aberta, conseguimos calcular os ganhos relativos do sistema, que é a primeira coisa que o exercício pede da gente.
Como se trata de um sistema podemos usar a fórmula abaixo para calcular o ganho :
Sunstituindo os valores encontrados anteriormente, teremos:
A matriz de ganhos relativos, também conhecida como RGA, poderá ser definida completamente conforme abaixo:
Sendo .
Portanto:
Para determinar o emparelhamento precisamos ver qual o ganho relativo está mais próximo de . Como é mais próximo de do que , o melhor emparelhamento será o 1-1/2-2.
Passo 3
Vamos agora calcular os desacopladores. Como o emparelhamento é do tipo 1-1/2-2, as fórmulas que usaremos para projetar esses desacopladores serão as que estão dadas abaixo:
Substituindo as funções de transferência que foram dadas no enunciado teremos:
Resposta
Emparelhamento 1-1/2-2
Exercício Resolvido #7
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 407, Problema 12-9.
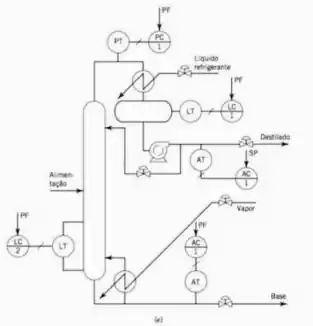
Na coluna de destilação da figura abaixo os fluxos de refluxo e de vapor para o refervedor são manipulados para controlar as purezas do produto destilado e da base. Testes em degrau de malha aberta em cada uma dessas variáveis manipuladas resultam nas seguintes funções de transferência:
One é a composição da porção pesada no destilado, é a composição da porção leve na base, em , e e são os sinais para as válvulas de refluxo e de vapor em . Os parâmetros de tempo estão em horas.
- Calcule os ganhos relativos para este sistema e determine o modo correto de emparelhar as variáveis controladas e manipuladas. As malhas se ajudam ou lutam entre si?
- Faça o diagrama de blocos e o projeto dos desacopladores para este sistema.
Passo 1
Esse exercício tem um monte de informação o que acaba confundindo a gente um pouco. Mas a gente pode dar uma filtrada no que realmente importa.
O fluxograma é bacana para entender melhor o que tá acontecendo e tal mas ele não é super importante para a resolução do exercício.
O que realmente vai importar para nós são as funções de transferência que relacionam cada uma das saídas com as entradas.
Mas porque essas equações são importantes?
Porque a partir dessas equações nós conseguimos encontrar os ganhos em malha aberta e com os ganhos em malha aberta a gente determina quase tudo que o exercício pede da gente.
Os ganhos em malha aberta são as constantes que multiplicam as funções de transferência, sendo assim, a gente consegue montar nossa matriz de ganhos em malha aberta:
Passo 2
Com a matriz de ganhos em malha aberta, conseguimos calcular os ganhos relativos do sistema, que é a primeira coisa que o exercício pede da gente.
Como se trata de um sistema podemos usar a fórmula abaixo para calcular o ganho :
Sunstituindo os valores encontrados anteriormente, teremos:
A matriz de ganhos relativos, também conhecida como RGA, poderá ser definida completamente conforme abaixo:
Sendo .
Portanto:
Boa, já conseguimos a primeira coisa que foi pedido. A segunda é se as malhas se ajudam ou lutam entre sim, que é o mesmo que perguntar se a interação é positiva ou negativa.
Como os ganhos relativos são maiores que ou negativos, dizemos que a interação é negativa, ou seja, elas lutam entre si.
Passo 3
Agora precisamos projetar os desacopladores. Para isso primeiramente vamos ver qual o tipo de interação entre as malhas.
Olhando a matriz de ganhos relativos, podemos ver que o melhor emparelhamento é o do tipo 1-1/2-2. Sendo assim, os desacopladores terão a seguinte fórmula:
Nós podemos pegar essas funções de transferência nas equações que foram dadas pra nós no enunciado, então teremos:
Sendo assim teremos os descopladores:
O decoplador possui um atraso negativo, e isso é fisicamente irrealizável, sendo assim, nós vamos deicar ele apenas como a constante:
Já o desacoplador possui um avanço, que é o termo . Isso não é muito problemático, mas para melhorar o desempenho é legal adicionar nem que seja um atrasozinho. Sendo assim, vamos colocar um atraso pequeno de e acrescentar esse valor no avanço também:
Passo 4
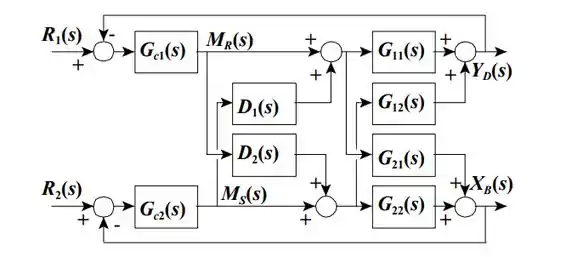
Por último, vamos ver como fica o diagrama de blocos do processo.
D_2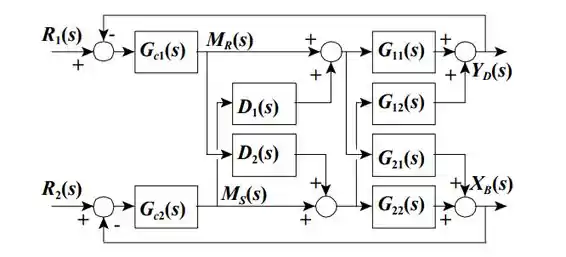
Repare que as malhas estão emparelhadas de forma 1-1/2-2, ou seja, a saída controla e a saída controla .
A entrada ainda assim impacta a sápida através do bloco mas essa interferência é atenuada pelo descoplador , que é o que nós calculamos lá em cima. O mesmo acontece para a entrada .
Resposta
Emparelhamento 1-1/2-2
Interação negativa
Exercício Resolvido #8
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 407, Problema 12-10.
Um processo tem duas variáveis controladas que são afetadas por duas variáveis manipuladas e um distúrbio . As funções de transferência são:
Onde:
- Calcule os ganhos relativos e selecione o correto emparelhamento para o sistema.
- Projete os desacopladores para este sistema.
Passo 1
Esse é aquele clássico exercício que a gente olha e toma aquele susto né. Mas vem comigo que você vai ver que ele é mais simples do que parece.
Primeiramente vamos analisar as informações que temos disponível.
Nós temos duas variáveis controladas e duas entradas, ou seja, um sistema 2x2 igual a todos que viemos trabalhando até aqui. Além disso, essas variáveis controladas são impactadas por um distúrbio, mas esse distúrbio não afeta em nada na nossa resolução do exercício, então ele ta ali só pra confundir a gente. Vamos só ignorar o bonitão e prosseguir.
A primeira coisa que nós podemos fazer, é determinar a matriz dos ganhos em malha aberta. Esses ganhos podem ser encontrados nas funções de transferência do problema, eles são as constantes que multiplica cada uma das funções de transferência. Sendo assim:
Passo 2
Com a matriz de ganhos em malha aberta, conseguimos calcular os ganhos relativos do sistema, que é a primeira coisa que o exercício pede da gente.
Como se trata de um sistema podemos usar a fórmula abaixo para calcular o ganho :
Sunstituindo os valores encontrados anteriormente, teremos:
A matriz de ganhos relativos, também conhecida como RGA, poderá ser definida completamente conforme abaixo:
Sendo .
Portanto:
Com essa matriz a gente consegue definir o emparelhamento mais adequado. Como a gente precisa evitar ganhos relativos negativos, o melhor emparelhamento será o 1-2/2-1.
Passo 3
Por último, precisamos projetar os desacopladores.
Como o emparelhamento é do tipo 1-2/2-1 as fórmulas dos desacopladores serão:
Substituindo os valores que foram dados no enunciado teremos:
Temos um problema aqui com o descoplador porque ele apresentou um “tempo vivo”, ou seja, um termo exponencial positivo, o que é fisicamente irrealizável. Para contornar essa situação, podemos acabar com esse termo em exponencial e acoplar ele no nosso avanço:
Resposta
Emparelhamento 1-2/2-1