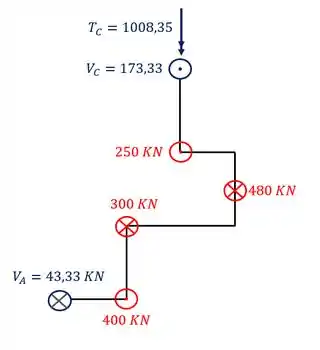
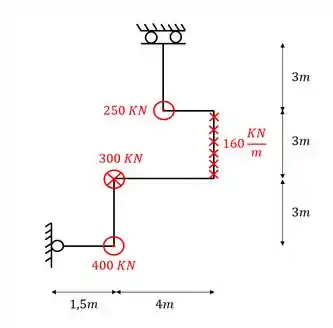
Dada a grelha abaixo, determine o valor das reações de apoio dela.
Passo 1
Sabemos que para resolver a nossa grelha, precisamos seguir uma sequência de passos muito importante, que irá funcionar da seguinte maneira
- Primeiro iremos fazer o balanceamento de incógnitas e equações presentes na nossa grelha.
- Em segundo lugar iremos fazer a troca dos apoios por vetores correspondentes a esses apoios
- Em terceiro lugar iremos trocar todas as cargas distribuídas por cargas concentradas para facilitar os cálculos
- Em quarto lugar calculamos o valor das reações de equilíbrio
- E por fim, quando o enunciado pedir, iremos calcular o diagrama de cortantes e momentos fletores, tendo em alguns casos o diagrama de torsor também. Alguns exercícios ao invés de pedir o diagrama irá pedir o momento e o cortante em pontos específicos, esse caso também se aplica ao ultimo estágio da nossa solução.
Entendido isso, bora aplicar esse conhecimento no nosso exercício.
Passo 2
Vemos que o primeiro passo consiste em fazermos o balanceamento de equações e incógnitas da nossa estrutura. Pra fazermos esse balanceamento precisamos saber o que temos de reação de apoio e de equação, vamos a contabilidade do número de equações primeiro
- Equações
- Incógnitas
- BARRA COM CARGA DISTRIBUÍDA
Sabemos que em grelhas nos ignoramos qualquer reação horizontal, já que não temos carregamento nessa direção, mas ainda temos 3 equações que são
Como não temos nenhuma rótula, significa que só temos 3 equações mesmo.
Primeiro temos um apoio do primeiro gênero, que nos dará 1 incógnita que será representada por
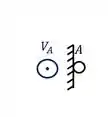
Eu chamo de V para indicar que é uma força Vertical.
O segundo apoio é um apoio do tipo dobradiça, que fornece duas reações, sendo uma reação vertical e uma reação de momento torsor, sempre perpendicular ao apoio de dobradiça.
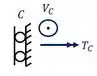
Nesse caso o que eu chamo de T é a nossa reação de Torsor.
Eu chamo de V para indicar que é uma força Vertical.
logo se fizermos a contabilidade de incógnitas e equações veremos que temos
O que caracteriza uma estrutura isostática, vimos bem essas definições nas aulas de pórticos, vigas e treliças, e sabemos que aqui só resolveremos estruturas isostáticas.
Passo 3
Como vimos, na sequência de passos, devemos trocar o nosso apoio por reações nos sentidos e direções corretas, dessa forma a nossa estrutura ficará da seguinte maneira
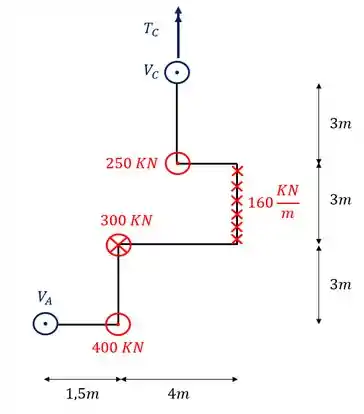
Passo 4
Sabemos que na sequência de passos, devemos trocar todas as cargas distribuídas por cargas concentradas, dessa forma, teremos que
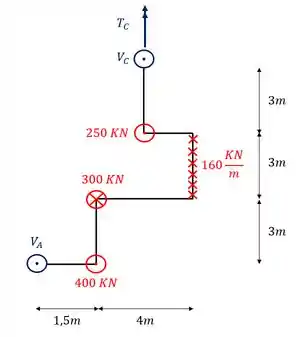
Para isso apenas precisamos fazer o seguinte cálculo
Dessa forma a nossa barra ficará da seguinte maneira
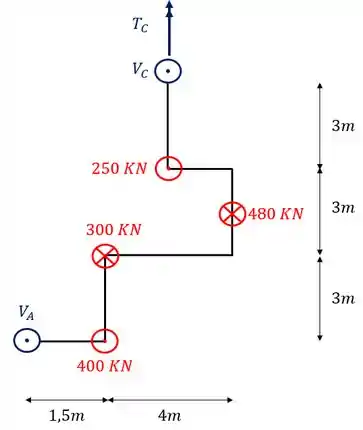
Passo 5
O próximo passo da nossa sequência é exatamente o cálculo das reações de apoio. Sabemos que o cálculo das reações de apoio usará as formulas de equilíbrio que destacamos lá em cima, mas temos que tomar muito cuidado com os braços de alavanca, por isso vamos tomar bastante cuidado, vamos fazer cada fórmula de cada vez
Sabemos que para termos equilíbrio devemos saber que o somatório de momentos em qualquer ponto da nossa barra deve ser zero, com isso, o ponto que iremos escolher é o ponto C que representa a nossa dobradiça. Dessa forma teremos
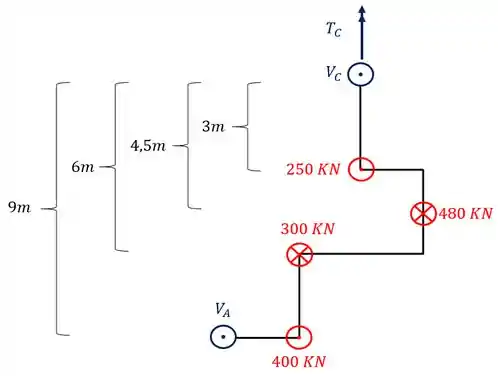
Perceba que nesse caso, todos os braços de alavancas de momento fletor, são perpendiculares ao apoio, todas as forças devem multiplicar o braço de alavanca correspondente. Com relação aos sinais eu arbitro positivo pra direita e negativo pra esquerda, mas você tem liberdade da escolha dos sinais. Sabendo de tudo isso, o nosso equilíbrio de momentos fletores será
Como é negativo devemos apenas inverter o vetor, para assim usarmos o momento com valor positivo que conhecemos, dessa forma teremos que
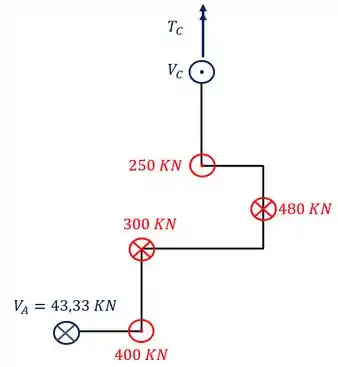
Vamos a próxima equação de equilíbrio.
Nesse caso não precisamos de braços de alavancas, só somar e subtrair as forças, considerando sair do papel positivo e entrar no papel negativo, teremos que
Agora para terminarmos todas as reações de apoios falta apenas determinarmos o valor do momento torsor no nosso apoio, e como é momento, novamente precisamos dos baços de alavancas, mas pense só, se no momento fletor o braço de alavanca é perpendicular, então no momento torsor os braços de alavancas serão paralelos, e no caso teremos no nosso exemplo os seguintes braços de alavanca.
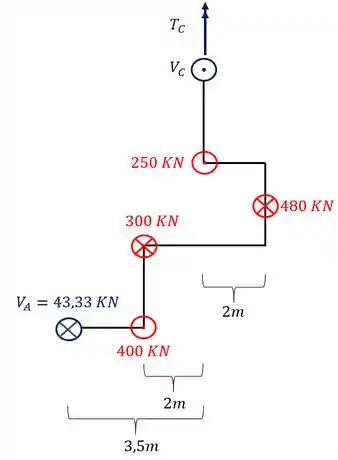
Com relações aos sinais eu considero positivo todos os torques que estiverem pra cima e negativo todos que estiverem para baixo. Assim sendo teremos que
Assim temos todas as reações de apoios, lembrando de inverter o sentido do torsor, que são dadas por
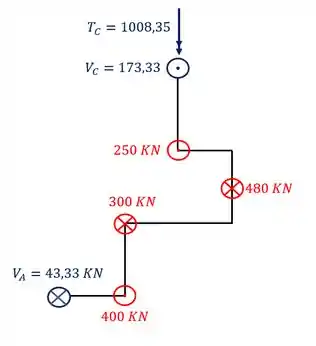
Resposta