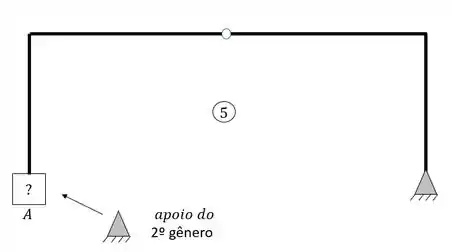
Para o pórtico composto abaixo determine qual seria a sua melhor separação e diga qual seriam os melhores apoios a serem colocados no ponto A para que o pórtico seja isostático.
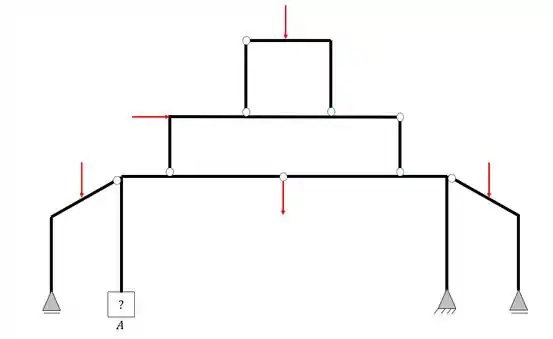
Passo 1
Antes de qualquer coisa temos que relembrar o nosso passo a passo para resolver esse tipo de problema. Para isso temos que respeitar algumas regrinhas, que são
- Um pórtico composto é formado por pórticos simples, que podem ser separados e resolvidos separadamente
- Somente podemos separar pórticos simples quebrando em rótulas, pois rótulas sempre darão apoios fictícios do segundo gênero (lembrando que apoios do segundo gênero são aquelas que possuem reações verticais e horizontais)
- A solução dos pórticos tem uma ordem: devemos começar pelos pórticos que se apoiam em outros, ou seja, os mais externos, e em seguida resolvemos os pórticos que recebem esses apoios, considerando a ações desses apoios.
- A consideração da reação de um apoio fictício em outro pórtico simples, deve ser sempre considerada com o sentido invertido.
- Essas regras devem sempre garantir que os pórticos, mesmo que separados, sejam isostáticos, isso é importante pois alguns professores gostam de perguntar qual tipo de apoio podemos adicionar ou não ao nosso pórtico. Por isso primeiro iremos fazer a separação do pórtico e só depois iremos determinar quais apoios devemos colocar.
- Por fim, já tendo a separação do pórtico composto em estruturas mais simples, iremos resolver primeiro as estruturas mais externas, calculando valores como, normal, cortante e momento fletor quando esses forem pedidos, e por fim iremos transferir as reações dos pórticos simples externos para os pórticos simples internos, nesse caso teremos resolvido completamente um exercício que cobre os diagramas ou esforços internos de todas as barras do pórtico.
Vale lembrar que o nosso problema não usará todo esse passo a passo, mas teremos questões mais complexas em que teremos que usar completamente o passo a passo dado acima.
Dito isso tudo, vamos aplicar nosso passo a passo no pórtico do nosso problema.
Passo 2
Como podemos ver, nosso pórtico é composto é precisamos separa-lo em pórticos mais simples. Para isso faremos o seguinte.
Sabemos que pra quebrarmos um pórtico composto em pórticos mais simples, precisamos, sempre, quebrar o pórtico nas rótulas. Por isso iremos primeiro marcar todas as rótulas do nosso pórtico.
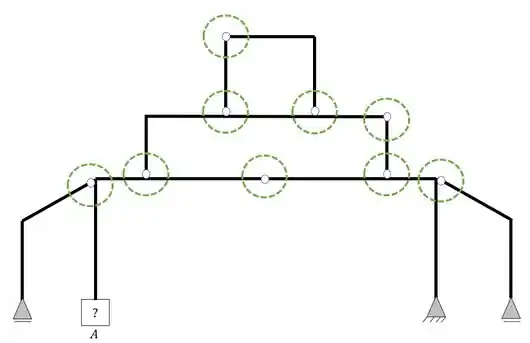
Marcada todas as rótulas, precisamos ter em mente que sempre que quebrarmos uma rótula trocaremos a rótula quebrada por um apoio do segundo gênero e precisamos garantir que a estrutura que sempre aparecer mais simples deve ser obrigatoriamente isostática. Dessa forma teremos que as rótulas mais viáveis a serem quebradas serão as marcadas em vermelho abaixo
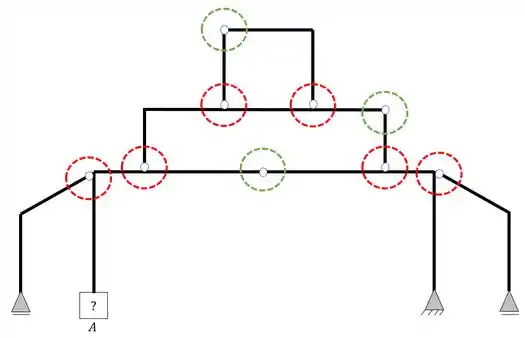
Mas perceba, foi dito que são as possíveis rótulas que podem ser quebradas porque aparentemente quebrando essas rótulas teremos estruturas mais simples, mas ainda temos que analisar se a estrutura será isostática. Definido os pontos de quebra, vamos a separação das estruturas.
Passo 3
Começando de cima pra baixo vemos que a primeira estrutura a ser formada é a que mostramos abaixo
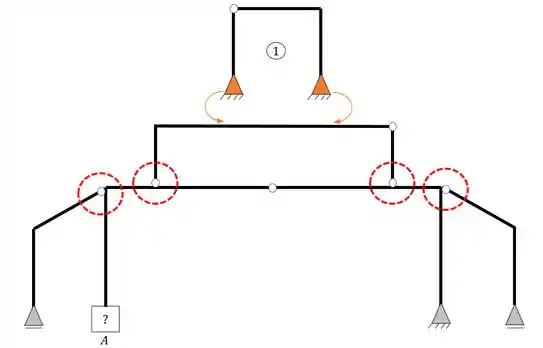
Sabemos que cada apoio do segundo gênero fornece duas incógnitas e que como a estrutura possui dois apoios do segundo gênero, no total, teremos, 4 incógnitas.
Quanto ao número de equações, sabemos que temos 3 de equilíbrio, e que uma rótula com 2 barras fornece mais uma equação. Assim podemos dizer que temos também 4 equações. Logo, se temos 4 incógnitas e 4 equações, tendo um vetor em cada direção, temos uma estrutura do tipo isostática, logo, a separação que fizemos está coerente. Vamos a próxima separação.
Passo 4
Continuando de cima pra baixo vemos que a segunda estrutura a ser formada é a que mostramos abaixo
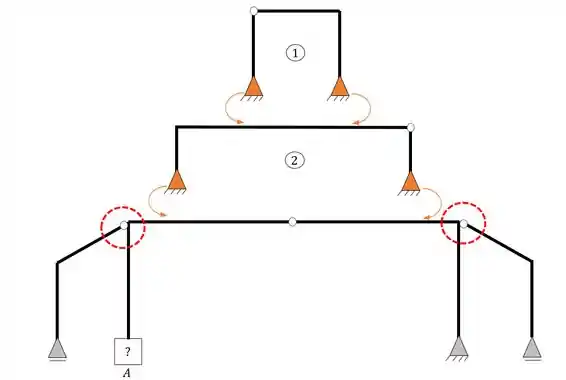
Sabemos que cada apoio do segundo gênero fornece duas incógnitas e que como a estrutura possui dois apoios do segundo gênero, no total, teremos, 4 incógnitas.
Quanto ao número de equações, sabemos que temos 3 de equilíbrio, e que uma rótula com 2 barras fornece mais uma equação. Assim podemos dizer que temos também 4 equações. Logo, se temos 4 incógnitas e 4 equações, tendo um vetor em cada direção, temos uma estrutura do tipo isostática, logo, a separação que fizemos está coerente. Vamos a próxima separação.
Passo 5
Agora vindo pela lateral vemos que a terceira e quarta estrutura a ser formada é a que mostramos abaixo
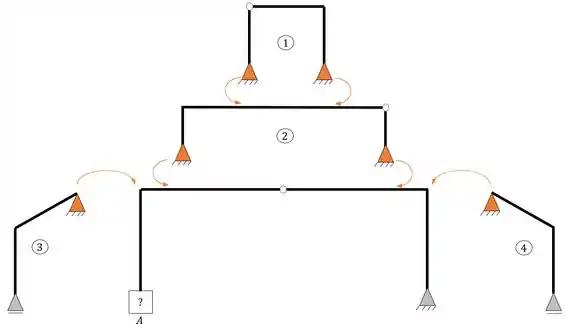
Sabemos que cada apoio do segundo gênero fornece duas incógnitas e que como a estrutura possui dois apoios do segundo gênero, no total, teremos, 4 incógnitas.
Quanto ao número de equações, sabemos que temos 3 de equilíbrio, e que uma rótula com 2 barras fornece mais uma equação. Assim podemos dizer que temos também 4 equações. Logo, se temos 4 incógnitas e 4 equações, tendo um vetor em cada direção, temos uma estrutura do tipo isostática, logo, a separação que fizemos está coerente. Vamos a próxima separação.
Passo 6
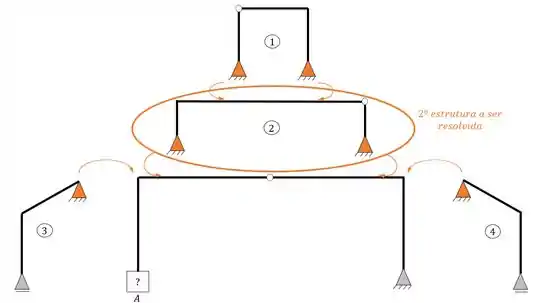
Como podemos ver conseguimos separar toda a nossa estrutura, faltando apenas definirmos uma ordem de solução e um apoio para o nosso ponto A. começando pela ordem de solução, sabemos que sempre iremos começar por estruturas que estão apoiadas em outras, ou seja, sempre iremos começar do pórtico simples mais externo até chegarmos no pórtico simples mais interno, então a nossa ordem de solução será.
- Primeira estrutura a ser resolvida
- Segunda estrutura a ser resolvida
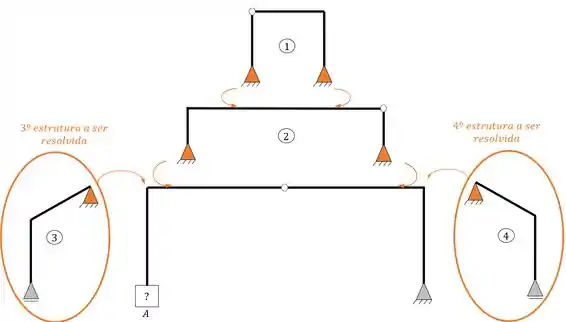
- Terceira e quarta estruturas a serem resolvidas
- Quinta estrutura a ser resolvida
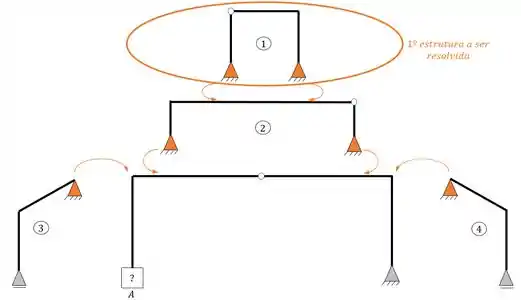
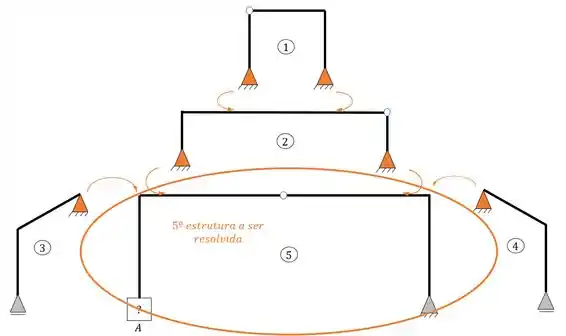
E por fim só falta analisarmos a quinta estrutura para definirmos o melhor apoio que podemos usar no nosso pórtico.
Passo 7
Olhemos a quinta estrutura mais de perto
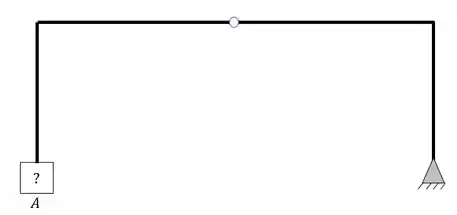
Podemos ver que ela possui um apoio do segundo gênero, o que sabemos que dará a nossa estrutura um total de 2 incógnitas.
Quanto ao número de equações, sabemos que temos 3 de equilíbrio e 1 devido a rótula com duas barras. Com isso temos um total de 4 equações.
Se temos 2 incógnitas e 4 equações, precisamos de mais 2 incógnitas para resolvermos o nosso problema, e como incógnita vem de apoio, precisamos de um apoio do segundo gênero para resolver a nossa estrutura, ou seja
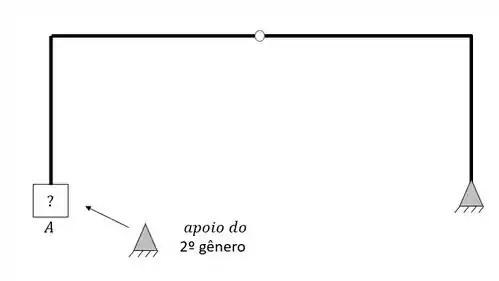
E assim resolvemos o nosso problema. Decidimos a sua melhor separação e ainda definimos o melhor apoio para a estrutura ser isostática, sendo nesse caso necessário um apoio do segundo gênero. Bora pro próximo exercício para ficarmos craques em separação de pórticos.
Resposta
Melhor separação e ordem de solução do pórtico
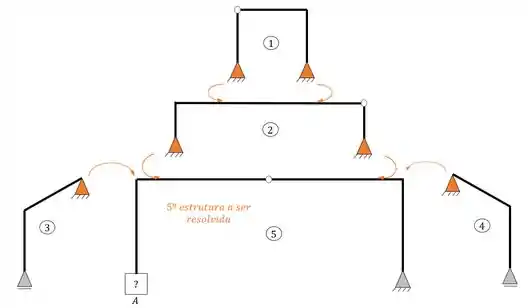
Apoio escolhido para o ponto A