Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
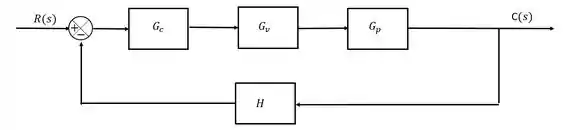
Determine o ganho e período finais sabendo que o controlador é do tipo proporcional e que:
Passo 1
Essa é aquela malha feedback mais clássica de todas, cuja função de trsnferência equivalente é a seguinte
Se você não se lembra como chegar nessa expressão, dá um revisadinha na aula de álgebra de diagrama de blocos, essa deduação tem que estar na ponta da língua.
Porém, para fazer a substituição direta precisamos mesmo é da equação característica, que é o denominador da função de transferência
Passo 2
Agora devemos substituir as funções de transferência do controlador e do processo na nossa equação característica:
Substituindo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Finalmente então, podemos aplicar a nossa substituição para encontrar o ganho e período finais:
Como:
Separando a parte real da imaginária e igualando as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo: