Um processo pode ser definido pela seguinte função de transferência:
Onde e são as constantes de tempo da válvula de controle e do transmissor, respectivamente. Considerando um controlador proporcional, encontre a faixa do ganho da malha, para a qual a malha é estável se e
Passo 1
Primeiramente devemos identificar noss malha para podermos encontrar a equação característica dela.
Como a função de transferência dada no exercício já envolve as dinâmicas da válvula e do transmissor, a malha pode ser simplificada da seguite maneira:
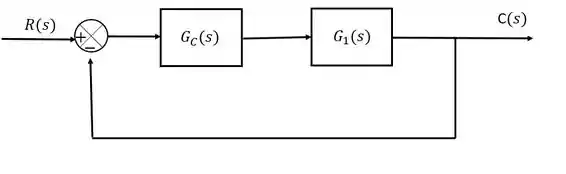
Onde é a função de transferência do processo, válvula e transmissor que foi dada no enunciada e é a função de transferência do controlador.
Como o enunciado diz que o controlador [e do tipo proporcional:
E como a malha é uma malha do tipo feedback, a função de transferência equivalente fica:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Com os valores das constantes dados, nossa função de transferência fica assim:
Substituindo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Uma vez que temos a equação característica bonitinha, o próximo passo é fazer a substituição:
Como:
Agora devemos separar a parte real da imaginária e igualar as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Portanto:
Passo 4
O enunciado pede que a gente encontre a faixa de estabilidade pra , entretanto achamos apenas o limite superior.
Para achar o limite inferior, usamos o critério dos coeficientes, que diz que para a malha ser estável todos os coeficientes devem possuir o mesmo sinal.
Sendo assim:
Portanto, a faixa de estabilidade para o ganho da malha é: