Um aço tem um limite de escoamento de 1100 MPa, um limite de resistência de 1200

MPa e uma tenacidade à fratura de 90 . Considere

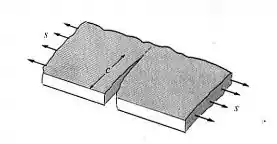
a) Uma placa com a configuração da figura abaixo, tem uma trinca passante de 2mm de comprimento. Ela vai quebrar antes de escoar ou escoar antes de quebrar?

b)Qual é o tamanho máximo de trinca que pode estar presente sem que a chapa frature antes de deformar?

Letra a)

Vamos calcular a tensão critica para os dados fornecidos:

Como a tensão critica está abaixo da tensão de escoamento o material irá fraturar antes de escoar.

Letra b)

Para que a placa fratura antes de deformar vamos considerar que a tensão critica seja de 1100MPa. Assim:

Obs.: Caso desejamos arredondar o valor para dois algarismo significativos devemos truncar o valor, pois caso arrendondemos para cima teremos um comprimento de trinca maior do que é possivel o comprimento critico. Logo: