Escalas de Temperatura e Lei Zero
Teoria
Temperatura
Quando uma balança com pesos em cada lado consegue se equilibrar e ficar parada, concluímos que esses dois objetos têm a mesma massa. Ou seja, seus valores iguais de massa fazem a balança parar de se movimentar.
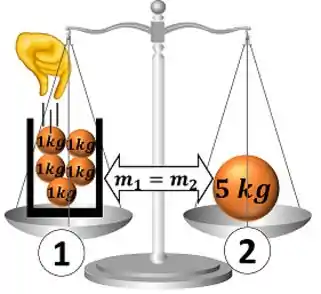
E quando dois blocos de metal param de esquentar ou esfriar, depois de ficarem algum tempo em contato? Eles passam a ter valores iguais de alguma outra propriedade? Sim! Quando isso ocorre, dizemos que eles têm o mesmo valor de temperatura ou que estão em equilíbrio térmico entre si. A temperatura é uma propriedade intensiva desses objetos.
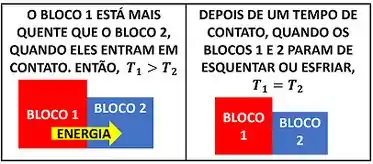
Se um bloco quente tiver contato com um bloco mais frio, eles vão trocar calor até pararem de esfriar e aquecer. Em outras palavras, se dois objetos com temperaturas diferentes entram em contato, eles trocam energia por calor até ficarem com temperaturas iguais. Ou seja, essa diferença de temperatura determina se tem ou não calor atravessando a fronteira do sistema!
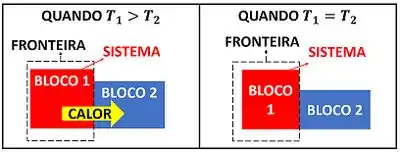
Por isso, para saber se a temperatura de um objeto é igual à temperatura de outro objeto, é só botar os dois em contato. Se as temperaturas já eram iguais, elas não vão variar. Se elas eram diferentes, vão diminuir ou aumentar até se igualarem. Mas como eu posso descobrir, se o Rio de Janeiro está tão quente quanto o deserto do Saara, se não consigo pôr os dois em contato?
Lei zero da termodinâmica
Podemos medir se a temperatura dos dois lugares são iguais, usando um objeto. A lei zero da termodinâmica diz que: se a temperatura desse objeto for igual às temperaturas do Rio de Janeiro e do deserto do Saara ao mesmo tempo, então, com certeza, o Rio de Janeiro e o Saara têm temperaturas iguais.
Falando isso de outra forma: se esse objeto tiver em equilíbrio térmico com o Rio de Janeiro e com o Saara ao mesmo tempo, podemos afirmar que o Rio de Janeiro está em equilíbrio térmico com o Saara. Isso funciona sempre que comparamos a temperatura de dois objetos, utilizando um terceiro objeto.
Para esse caso geral, que compara dois objetos, a lei zero diz que: quando dois corpos têm igualdade de temperatura com um terceiro corpo, eles terão igualdade de temperatura entre si.
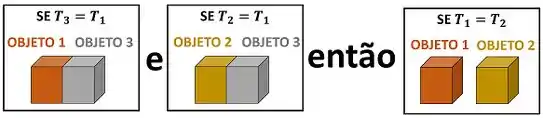
Em termodinâmica, chamamos esse terceiro objeto ou terceiro corpo de termômetro.
Escala de temperatura Celsius e escala de temperatura Fahrenheit
Como foi dito antes, testamos se dois objetos tinham temperaturas iguais, se elas não variarem, quando os dois estiverem em contato. Mas nem sempre podemos sentir essa alteração de temperatura, colocando nossa própria mão nos objetos. As vezes eles estão muito quentes! Então como podemos medir se existe essa mudança, sem usar o toque?
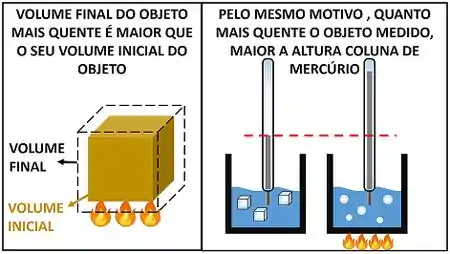
Aproveitando o fato de que um objeto aumenta de volume, quando é aquecido! Se usarmos como nosso termômetro recipiente de vidro com mercúrio líquido, o mercúrio vai expandir, com o aumento de , ou contrair, com a diminuição de . Essa alteração de volume gera uma alteração na altura da coluna de mercúrio no vidro. Dessa forma, conseguimos medir a temperatura e o quanto ela varia!
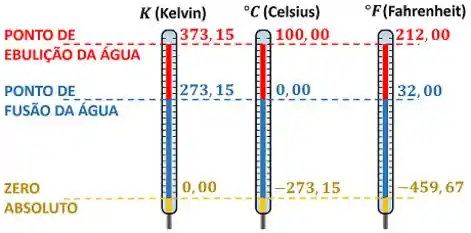
Chamamos as marcações presentes nos termômetros de escalas. As escalas de temperatura mais comuns são: a escala Celsius (utilizada no Sistema Internacional), a escala Fahrenheit e a escala Kelvin (também utilizada no Sistema Internacional).
Assim como usamos réguas com escalas diferentes para medir um mesmo tamanho, usamos termômetros com escalas diferentes para medir a mesma temperatura.
A escala de temperatura Celsius usa o grau Celsius como unidade. Já a escala de temperatura Fahrenheit usa o grau Fahrenheit como unidade. Para converter a unidade grau Fahrenheit para grau Celsius, usamos a seguinte fórmula:
Atenção! Se quisermos converter uma diferença de temperatura medida em grau Fahrenheit para uma diferença de temperatura em grau Celsius, precisamos usar outra equação:
onde é a diferença de temperatura.
Por essa expressão, vemos que:
Escala absoluta de temperatura
A grande diferença entre a escala Kelvin e as escalas mostradas antes, é que o valor de temperatura nula nessa escala tem um significado especial. Nenhum objeto pode alcançar um valor de temperatura menor que zero kelvin. Ou seja, ao contrário das outras escalas, a escala Kelvin não tem valor negativo de temperatura.
Além disso, a temperatura de zero kelvin é inatingível. Por ela ser um limite inferior da escala, é chamada de zero absoluto. Por esse mesmo motivo, a escala Kelvin é chamada de escala absoluta de temperatura.
A unidade Kelvin possui tamanho igual ao grau Celsius. Ou seja, o valor das diferenças de temperatura em kelvin é igual ao valor em grau Celsius.
Apesar de suas unidades possuírem o mesmo valor, os valores de temperatura medidos por elas são diferentes. A fórmula que converte uma temperatura em grau Celsius para uma em Kelvin é:
Ou seja, a temperatura de ebulição da água a pressão atmosférica vale:
Já o valor de temperatura de fusão da água a pressão atmosférica é:
Lei zero da termodinâmica
Escala de temperatura Celsius e escala de temperatura Fahrenheit
Escala absoluta de temperatura K e l v i n
Exercícios Resolvidos
Exercício Resolvido #1
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 49-1.89
Qual é o valor da temperatura absoluta (em Kelvin) equivalente a ?
Passo 1
O enunciado pede a conversão de uma temperatura de grau Celsius para kelvin .
A fórmula de conversão de uma escala de temperatura para outra é:
Ou seja, a temperatura em kelvin é igual à soma entre a temperatura em grau Celsius e .
Para descobrir o valor na escala Kelvin, temos que substituir o valor da temperatura em grau Celsius dada pelo enunciado nessa fórmula de conversão.
Passo 2
Resposta
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 49-1.90
A zona de conforto humana está entre e . Qual é a faixa de variação em Kelvin? Qual é a mudança relativa máxima da baixa à alta temperatura?
Passo 1
O enunciado fala que a faixa de temperatura, na qual um ser humano se sente confortável, inicia em e termina em . Ou seja, a diferença entre a temperatura mais quente e a temperatura mais fria desse intervalo é de:
O enunciado pede que calculemos o tamanho dessa faixa, quando as temperaturas são representadas em kelvin. Para isso, existe uma fórmula de conversão de diferença de temperatura, que converte a desigualdade em grau Celsius para uma desigualdade em kelvin.
Ou seja, a diferença de temperatura em kelvin é igual a diferença de temperatura em grau Celsius.
Passo 2
Por causa dessa igualdade, achamos:
Resposta
Exercício Resolvido #3
Michael A. Boles e Yunus A. Çengel, Thermodynamics: An Engineering Approach, 8ª ed. New York: McGraw-Hill Education, 2015, pp. 42-1.31C
Quais são as escalas de temperatura comuns e absolutas nos sistemas S.I. e inglês?
Passo 1
Para poder classificar cada escala de temperatura, dividiremos essa tarefa em três etapas:
- Listar as escalas de temperatura que são usadas no Sistema Internacional de Unidades (S.I) e as escalas que são usadas no sistema inglês
- Explicar a diferença entre escala comum e escala absoluta de temperatura.
- Classificar as escalas de cada grupo (S.I. e sistema inglês) entre escala comum e escala absoluta.
Passo 2
As escalas de temperatura utilizadas no sistema inglês são:
- Escala Fahrenheit. Sua unidade é o grau Fahrenheit
- Escala Rankine. Sua unidade é o rankine
- Escala Celsius. Sua unidade é o grau Celsius
- Escala Kelvin. Sua unidade é o kelvin
A conversão de uma temperatura de grau Fahrenheit para rankine é feita pela fórmula:
A fórmula que converte uma diferença de temperatura de grau Fahrenheit para rankine é:
Ou seja um grau Fahrenheit é igual a uma unidade na escala Rankine.
As escalas de temperatura utilizadas no Sistema Internacional de Unidades são:
A conversão de uma temperatura de grau Celsius para kelvin é feita pela fórmula:
A fórmula que converte uma diferença de temperatura de grau Celsius para kelvin é:
Ou seja um grau Celsius é igual a uma unidade na escala Kelvin.
Passo 3
Para saber se uma escala de temperatura é absoluta ou comum precisamos entender a diferença entre esses dois tipos.
As escalas de temperatura absolutas dão um sentido especial à temperatura nula. Para elas, a temperatura zero é um limite inferior da escala. Por causa disso, esse valor nulo é chamado de zero absoluto nesses casos. Por esse mesmo motivo, uma escala é classificada como absoluta.
Passo 4
Nas escalas Kelvin e Rankine, o zero é um limite inferior. Ele é absoluto. Por isso, essas duas escalas são escalas de temperatura absolutas.
Já nas escalas Celsius e Fahrenheit, o zero não é um limite inferior. Nelas, existem valores negativos de temperatura. Por isso, elas são escalas de temperatura comuns.
Resposta
Escala de temperatura comum usada no S.I: Escala Celsius.
Escala de temperatura absoluta usada no S.I: Escala Kelvin.
Escala de temperatura comum usada no sistema inglês: Escala Fahrenheit.
Escala de temperatura absoluta usada no sistema inglês: Escala Rankine.
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 50-1.95
A temperatura do ar na atmosfera cai com o aumento da altitude. Uma equação que fornece o valor local médio da temperatura absoluta do ar na atmosfera é , em que é a altitude em metros. Qual é a temperatura média do ar em um ponto localizado em uma altitude de ? Forneça seu resultado em graus Celsius e em kelvin.
Passo 1
O exercício mostra a variação da temperatura média do ar com a distância vertical em relação ao nível do mar . Ele faz isso, mostrando a expressão da temperatura em função dessa posição. O resultado dela está em temperatura absoluta. Logo, a resposta da equação está em kelvin.
Por fim, ele pede a temperatura média de todos os pontos do ar que estão a do solo em kelvin e em grau Celsius.
Para esse exercício:
Para transformar o resultado de kelvin para grau Celsius, usamos a seguinte fórmula:
Para achar o resultado em , substituímos por .
Passo 2
O valor da temperatura média é . Para achá-lo, vamos substituir na fórmula de temperatura.
Substituindo esse valor na fórmula de conversão para grau Celsius, obtemos:
Resposta
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 5ª ed. New York: McGraw-Hill Education, 2004, pp. 34-1.25C
O que é a Lei Zero da Termodinâmica?
Passo 1
A lei Zero da termodinâmica afirma que se um copo de água gelada tiver a mesma temperatura que a colher que colocamos dentro do copo e, ao mesmo tempo, essa colher tiver a mesma temperatura do sorvete que estamos comendo, isso quer dizer que a água gelada e sorvete têm a mesma temperatura! Tá, mas qual a importância disso?
Para responder o enunciado, precisamos entender a relevância desse fato para a termodinâmica. Por fim, precisamos conhecer a formal da Lei Zero.
Vamos deixar a resposta no nosso próximo passo, onde descobriremos o motivo de ela existir.
Passo 2
Essa lei é importante, porque nos permite comparar a temperatura de vários objetos sem eles entrarem em contato físico entre si. Se a colher do exemplo esquentasse, quando entrasse em contato com uma comida quente, saberíamos, por exemplo, que essa comida está mais quente que o sorvete e que a água gelada.
Além disso, conseguimos medir a temperatura desses três objetos a partir da variação das propriedades de um único objeto: a colher! Isso quer dizer que a Lei Zero não apenas permite a comparação de temperaturas sem contato térmico, mas também cria um objeto medidor de todas as temperaturas. Em outras palavras, a Lei Zero cria o termômetro!
Passo 3
Agora que já temos uma base, podemos introduzir formalmente o que diz essa lei: quando dois corpos têm igualdade de temperatura com um terceiro corpo, eles terão igualdade de temperatura entre si.
Dizendo isso de outra forma: quando dois corpos estão em equilíbrio térmico com um terceiro corpo, eles estão em equilíbrio térmico entre si.
Resposta
A lei zero permite a comparação de temperatura entre dois corpos sem colocá-los em contato e cria o conceito do termômetro, através do seguinte princípio: quando dois corpos têm igualdade de temperatura com um terceiro corpo, eles terão igualdade de temperatura entre si.
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 50-1.94
Elabore uma equação para a conversão de temperaturas de °F para °C. Utilize como base as temperaturas dos pontos de solidificação e de vaporização da água.
Passo 1
O exercício pede para que a gente deduza a seguinte fórmula de conversão da temperatura em grau Fahrenheit para a escala Celsius:
Mas por que ele diz para utilizarmos as temperaturas dos pontos de solidificação e de vaporização da água como base? Ele diz isso, porque, através da razão entre as diferenças dessas temperaturas, conseguimos criar uma relação entre as duas escalas.
Passo 2
Levando em conta o que o desenho mostra, descobrimos duas equações para as razões entre os tamanhos a e b.
Juntando as duas fórmulas temos:
Pronto! Achamos o motivo da fórmula de conversão ser daquela forma!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 50-1.92
Os termômetros de mercúrio indicam a temperatura pela medida da expansão volumétrica de uma massa fixa de mercúrio líquido. A expansão volumétrica é em virtude de variação da massa específica do mercúrio com a temperatura. Determine a variação percentual do volume ocupado pelo mercúrio quando a temperatura varia de para . Admita que a massa específica do mercúrio varie com a temperatura de acordo com:
onde está em .
Passo 1
O exercício quer saber a variação percentual de volume do mercúrio depois que ele aumenta de temperatura. Ou seja, temos que calcular:
onde:
- é a variação percentual de volume de mercúrio;
- é o volume de mercúrio, quando ele está a ;
- é o volume de mercúrio, quando ele está a .
Mas como podemos calcular cada volume? Reorganizando as fórmulas de massa específica:
sendo:
- , a massa específica do mercúrio, quando ele está a ;
- , a massa específica do mercúrio, quando ele está a ;
- , a massa de mercúrio.
Perceba que a massa de mercúrio não muda, quando ele expande! Isso é importantíssimo de ser notado, porque permite que a gente corte essa variável, quando formos calcular a variação relativa de volume .
Outro fato importante de ser observado é que as massas específicas são dadas indiretamente pelo enunciado a partir das equações:
onde:
- é a temperatura do mercúrio antes da sua expansão. Ela vale segundo o enunciado;
- é a temperatura do mercúrio depois da sua expansão. Ela vale segundo o enunciado.
Agora temos todas as informações necessárias para iniciarmos os cálculos, substituindo os dados.
Passo 2
Iniciamos os cálculos com a substituição dos valores de temperatura para achar as massas específicas:
Agora usamos os valores encontrados na fórmula dos volumes para encontrá-los em função da massa de mercúrio .
Substituindo essas expressões na fórmula de variação percentual de volume, temos:
Rearranjando a fração, achamos:
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 50-1.93
A massa específica da água líquida é calculada por:
sendo a temperatura da água em . Se a temperatura se eleva em , qual é a elevação da espessura de uma lâmina de água de ? Considere que a água estava à temperatura ambiente antes do seu aquecimento.
Passo 1
O exercício quer saber a variação da altura do filme de água depois que ele aumenta de temperatura. Para facilitar nossa vida, podemos visualizar o problema de acordo com a imagem abaixo.
Ou seja, podemos considerar que o volume do filme de água aumenta sem aumentar a área da sua base. Em outras palavras, apenas a sua altura varia com essa expansão.
Para conectar as informações dadas, calculamos a variação relativa de volume do filme de duas formas e depois igualar os resultados encontrados pelos dois caminhos.
Pela primeira forma, nós vamos calcular geometricamente, considerando o volume igual à área da base do filme multiplicada pela sua altura.
onde:
- é a variação do volume de água;
- é o volume de água, quando ela está a ;
- é o volume de água, quando ela está a ;
- é a altura do filme de água, quando ela está a . O enunciado diz que ela vale ;
- é a altura do filme de água, quando ela está a ;
- é a variação da altura do filme de água. Essa é a incógnita do problema.
- é a área do filme de água.
A segunda forma de calcular a variação relativa de volume será o nosso próximo passo.
Passo 2
Pela segunda forma, vamos calcular termodinamicamente, considerando o volume como a divisão entre a massa da água e a sua massa específica. Temos que lembrar também que a massa de água não se altera durante sua expansão.
onde:
- , a massa específica da água, quando ela está a ;
- , a massa específica d aágua, quando ela está a ;
- , a massa de água.
Depois de igualar as duas equações de variação relativa de volume do filme e reorganizar a fórmula, encontramos uma expressão para a variação de altura .
As massas específicas são dadas indiretamente pelo enunciado a partir das equações:
onde:
- é a temperatura da água antes da sua expansão. Ela vale segundo o enunciado;
- é a temperatura da água depois da sua expansão. Ela vale segundo o enunciado.
Agora temos todas as informações necessárias para iniciarmos os cálculos, substituindo os dados.
Passo 3
Iniciamos os cálculos com a substituição dos valores de temperatura para achar as massas específicas:
Agora usamos os valores encontrados na fórmula da variação da altura do filme.