Fases e Substância Pura
Produzido por Rafael Cardoso BrandãoTeoria
O que é uma fase?
Se a gente tentar encher um pote cilíndrico com cubos de gelo, ele não vai ocupar todo o volume do recipiente. Se quisermos fazer a mesma coisa com água líquida, ela vai conseguir preencher tudo, dependendo de quantos litros colocamos. Mas se a gente fizer isso com vapor d’água, ele sempre vai completar todo o espaço do pote. Mesmo se a gente pôr pouco vapor.
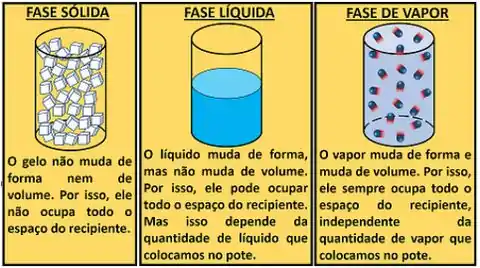
Por que os resultados são tão diferentes, se nos três casos estamos colocando a mesma substância (água) no pote? Porque em cada um dos exemplos, as moléculas estão organizadas de formas diferentes dentro da água! Chamamos essas formas diferentes de organização molecular de fases.
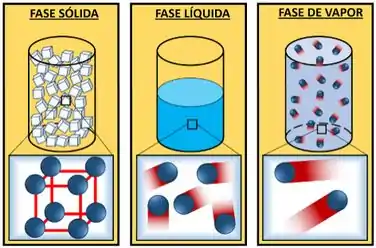
Fase sólida
Por exemplo, as moléculas do gelo estão muito perto umas das outras. Além disso, elas estão quase presas em uma posição fixa. Chamamos esse tipo de organização de fase sólida. Por causa dessa proximidade, o volume específico dessa fase é muito pequeno.
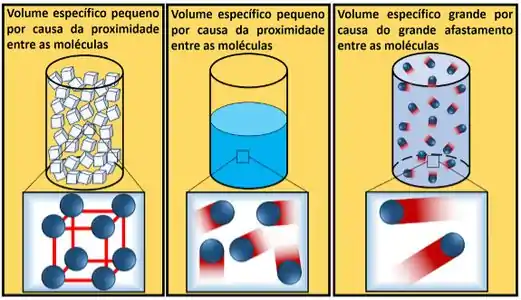
Como os átomos quase não se mexem, o gelo praticamente não muda de formato e de tamanho. Por isso, o seu volume específico praticamente não varia com a pressão! Em outras palavras, é tão difícil de comprimir a fase sólida por pressão, que as vezes consideramos que o sólido é incompressível. Ou seja, seu volume não depende da pressão. Só da temperatura.
onde é o volume específico do sólido e é uma função que calcula o valor do volume específico do sólido, quando sabemos o valor de temperatura.
Fase líquida
Na fase líquida, as moléculas quase não aumentam a distância entre si, se compararmos com o espaço entre os átomos de uma fase sólida. Por isso, geralmente o volume específico do líquido é um pouco maior que o volume específico do sólido.
onde é o valor do volume específico do líquido.
Mas atenção! Esse aumento de volume específico não ocorre para todas as substâncias. No caso da água, o volume específico da fase líquida é menor que o volume específico do gelo.
onde é o volume específico do gelo e é o volume específico da água líquida.
Apesar de existir essa diferença entre líquido é sólido, eles têm uma característica em comum: os valores dos seus volumes específicos quase não variam com a pressão. Eles mudam mais com a alteração da temperatura. Ou seja, os dois podem ser considerados incompressíveis.
onde é uma função que calcula o valor do volume específico do líquido através do valor de temperatura.
Fase de vapor
O volume específico do vapor d’água a é vezes maior que o volume específico da água líquida a mesma temperatura. Esse aumento significativo do volume do líquido para o volume do vapor se repete para todas substâncias! Isso ocorre, porque as moléculas do vapor estão bem mais agitadas e distantes umas das outras.
onde é o volume específico do vapor.
Se apertarmos o êmbolo de uma seringa cheia de vapor d’água, conseguimos comprimir seu volume facilmente. Por que não encontramos a mesma facilidade, comprimindo uma seringa com água líquida?
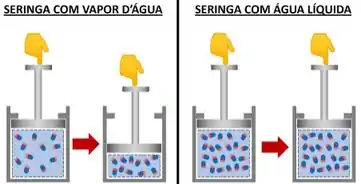
Isso acontece, porque, ao contrário das fases líquida e sólida, o vapor é uma fase compressível. Ou seja, seu volume específico varia bastante com a alteração da pressão e da temperatura. Resumindo, o valor do volume específico é uma função da temperatura e da pressão.
onde é a função que calcula o valor de volume específico, quando conhecemos os valores de temperatura e pressão.
Volume específico de uma mistura de líquido com vapor
Nem sempre estamos estudando um sistema formado por uma única fase. Por exemplo: se quisermos estudar a água líquida fervendo na panela, vamos ter que aprender a lidar com uma mistura entre a fase líquida e o vapor d’água sendo gerado. Então como podemos calcular o volume específico médio dessa mistura para simplificar nossa análise?
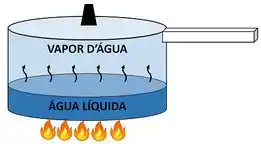
O volume específico médio é igual ao volume total dividido pela massa total.
onde:
- é o volume específico médio da mistura de líquido com vapor
- é o volume total, calculado como a soma dos volumes ocupados pelas duas fases
- é a massa total, calculada como soma das massas de cada fase
sendo:
- , o volume ocupado pelo líquido
- , o volume ocupado pelo vapor
onde:
- , a massa de líquido
- , a massa de vapor
O volume de cada fase pode ser encontrado, reorganizando as fórmulas de volume específico para o líquido e para o vapor.
Substituindo essas expressões de volume na fórmula de volume total, temos que:
Por fim, usando esse resultado na equação de volume específico médio, achamos:
Rearranjando a fórmula:
Exercício de cálculo do volume específico médio
Agora que nós temos uma equação de volume específico médio prontinha, por que não usamos ela, resolvendo um problema?

Qual o volume específico médio de uma mistura entre água líquida e vapor d’água, sabendo que da massa total é composta de vapor e que o volume específico do líquido vale e o do vapor vale ?
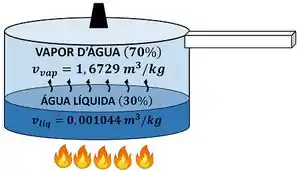
Como podemos fazer o cálculo, se o problema não nos deu as massas de cada componente? Olhando bem para a fórmula final de volume específico médio! Ela não precisa dos valores de massa para ser resolvida. Ela só exige que a gente tenha a massa de cada fase sobre a massa total e . O enunciado nos deu essa informação através da porcentagem!
Se o vapor é da massa total, sobrou apenas da massa total para o líquido.
Os outros dados passados pela questão são os valores de volume específico de casa fase:
Substituindo os valores na equação, encontramos o volume específico médio da mistura:
Título da mistura bifásica
Quando o líquido está mudando de fase para vapor, o sistema fica dividido em duas partes: massa de vapor e massa de líquido. A razão entre a massa de vapor e a massa total da mistura bifásica é chamada de título.
Essa variável pode ser considerada uma propriedade termodinâmica intensiva! Mas cuidado! Existe uma condição para ela ser classificada desse jeito: a substância deve estar na temperatura de mudança de fase correspondente a sua pressão.
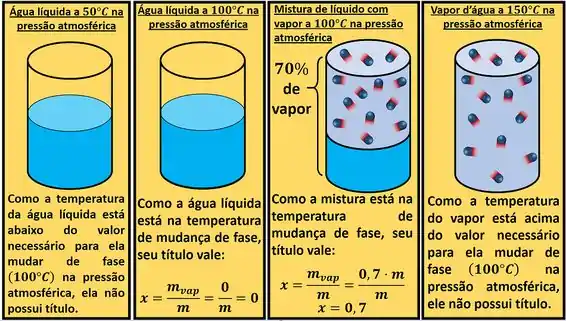
Por exemplo: quando a água estiver na pressão atmosférica, ela só se transforma em vapor a . Ou seja, ela só terá um título, se estiver a de temperatura.
Atenção! Como o título é uma divisão de duas massas, ele não possui unidade!
Se a gente substituir a fórmula do título na equação do volume específico médio :
Dessa forma encontramos uma fórmula de que cai muito em prova!!
Substância pura e substância simples compressível
Existe uma infinidade de fatores que podem influenciar no valor de volume específico de uma substância. Por exemplo: a água fica mais densa, quando é misturada com sal. Por isso, conseguimos boiar sem esforço em mares extremamente salgados, como o Mar Morto.

Mas como podemos desconsiderar os efeitos da concentração de sal na água para simplificar o cálculo de suas propriedades? Focando nossos estudos apenas em água pura! Ou seja, considerando que estamos estudando apenas substâncias com composição química igual em todas as suas fases!
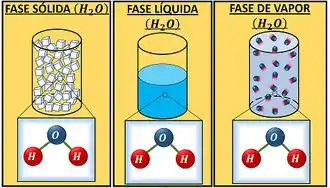
Em termodinâmica, chamamos essas substâncias com composição química constante em todas as fases de substâncias puras. A água salgada não é uma substância pura, porque geramos um vapor com menos sal, quando a esquentamos. Isso ocorre, porque a água evapora antes do sal, produzindo um vapor com composição diferente em relação ao líquido.
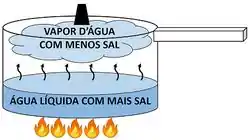
Ótimo! Conseguimos nos livrar dos efeitos da composição da substância sobre os cálculos de propriedades! Mas como podemos ignorar os outros fatores complicados que influenciam o movimento das moléculas de uma substância pura (efeitos superficiais, magnéticos e elétricos)?

Focando nossos estudos em um tipo específico de substância pura: a substância simples compressível. Nestas substâncias, os efeitos de superfície, magnéticos e elétricos têm um impacto tão pequeno sobre o seu comportamento, que podem ser desprezados!
A água pura é uma substância simples compressível!